
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Учебно-методическое обеспечение
|
|
|
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
Задания к выполнению работы
Решение
Пример 1.27
Решение
Пример 6.4
Решение
Пример 6.3.
Метод Вонга
Метод Вонга – метод, в котором используется сконструированная конъюктивно-дизъюнктивная нормальная форма представления исходной клаузы, являющейся клаузой Вонга  , а процедура доказательства сводится к последовательному разбиению дизъюнкций или конъюнкций таким образом, чтобы слева и справа от метаимпликации появилась одна и та же буква Х.
, а процедура доказательства сводится к последовательному разбиению дизъюнкций или конъюнкций таким образом, чтобы слева и справа от метаимпликации появилась одна и та же буква Х.
В клаузе Вонга переменная Х пробегает некоторые буквы, входящие в клаузу, а 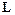 и
и  - определенные комбинации дизъюнктов и конъюнктов.
- определенные комбинации дизъюнктов и конъюнктов.
Разберем метод Вонга на примере доказательства справедливости правила отделения
 или
или  .
.
Здесь имеется только одна дизъюнкция, которую можно подвергнуть разбиению. После ее разбиения получим две новых клаузы
 и
и  или
или  .
.
Вторая клауза удовлетворяет и аксиоме порядка, и клаузе Вонга. В качестве Х в ней выступает  , а
, а  и
и  .
.
Первая клауза тоже будет удовлетворять необходимым требованиям, но только после того, как терм  из левой части клаузы с противоположным знаком перенести в правую часть. Такой перенос справедлив, поскольку, перейдя к объектным логическим операциям, а затем обратно, можно выполнить следующие преобразования:
из левой части клаузы с противоположным знаком перенести в правую часть. Такой перенос справедлив, поскольку, перейдя к объектным логическим операциям, а затем обратно, можно выполнить следующие преобразования: 
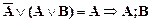 . Тогда будем иметь
. Тогда будем иметь
 где
где  и
и  .
. 
При большом числе букв в исходной клаузе прибегают к специальной нумерации производных клауз, чтобы не запутаться.
Установить справедливость следующей клаузы:
 .
.
Сначала приведем ее в соответствующую конструктивно-дизъюнктивную нормальную форму

 .
.
Далее производим разбиение первой дизъюнкции  , умножая ее на оставшуюся часть левого выражения (
, умножая ее на оставшуюся часть левого выражения ( и получим две производные клаузы:
и получим две производные клаузы:
|
|
|
1. 
2.  .
.
Клаузу (1) можно отбросить, так как она уже удовлетворяет клаузе Вонга (Х содержится и в левой, и в правой части клаузы). Вторую дизъюнкцию необходимо разбивать дальше. Для этого дизъюнкцию  умножим на оставшуюся часть левого выражения
умножим на оставшуюся часть левого выражения  и получим три клаузы:
и получим три клаузы:
2.1.  ,
,
2.2.  ,
,
2. 3.  .
.
Произведем разбиение первой клаузы, то есть перемножим выражение  на выражение в скобках
на выражение в скобках  , получим три клаузы
, получим три клаузы
2.1.1.  – клауза Вонга, так как
– клауза Вонга, так как  ,
,
2.1.2. 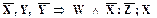 , после переноса
, после переноса 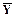 вправо получим клаузу Вонга
вправо получим клаузу Вонга  , в которой
, в которой  ,
,
2.1.3.  , после разбиения дизъюнкта
, после разбиения дизъюнкта  получим клаузы Вонга
получим клаузы Вонга  и
и  , в которых
, в которых  и
и  соответственно.
соответственно.
Рассмотрим теперь клаузу 2.2. Произведем ее разбиение аналогично клаузе 2.1 и получим
2.2.1.  , где
, где  ,
,
2.2.2.  , где (
, где (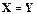 после переноса
после переноса  вправо). Эти две клаузы удовлетворяют клаузе Вонга. Рассмотрим третью.
вправо). Эти две клаузы удовлетворяют клаузе Вонга. Рассмотрим третью.
2.2.3.  .
.
В этой клаузе нужно разбить конъюнкцию правой части, поскольку в левой части нет букв, соответствующих буквам этой конъюнкции. Сначала в клаузе 2.2.3 упростим ее левую часть, так как  , то
, то  .
.
После разбиения получим
2.2.3.1. 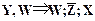 , 2.2.3.2.
, 2.2.3.2.  .
.
(Разбиение идет по следующей схеме. Так как в соответствии с причинно-следственным отношением (6.1), если в метаимпликации (2.2.3) посылка  истинна, то истинно и следствие
истинна, то истинно и следствие  , которое представляет собой конъюнкцию. Следовательно, истинны оба члена конъюнкции и
, которое представляет собой конъюнкцию. Следовательно, истинны оба члена конъюнкции и  и
и  , отсюда и результат разбиения, который приведен выше).
, отсюда и результат разбиения, который приведен выше).
Клауза 2.2.3.1 уже соответствует клаузе Вонга, в ней  , а клаузу 2.2.3.2 сначала немного преобразуем, перенеся из правой части
, а клаузу 2.2.3.2 сначала немного преобразуем, перенеся из правой части  в левую с отрицанием, и получим клаузу
в левую с отрицанием, и получим клаузу  , имеющую вид клаузы Вонга, в которой
, имеющую вид клаузы Вонга, в которой  .
.
Осталась еще одна ветвь (2.3) не доказанная нами на соответствие клаузе Вонга. Она отличается от рассмотренных наличием непарной переменной  , которая тем не менее не может повлиять на конечный результат. Разбиение клаузы будет идти аналогично рассмотренной процедуре.
, которая тем не менее не может повлиять на конечный результат. Разбиение клаузы будет идти аналогично рассмотренной процедуре.
Произведем разбиение третьей клаузы (2.3), то есть перемножим выражение  на выражение в скобках
на выражение в скобках  , получим три клаузы
, получим три клаузы
|
|
|
2.3.1.  – клауза Вонга, где
– клауза Вонга, где  .
.
2.3.2.  , где
, где 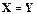 после переноса
после переноса  вправо, то есть это тоже клауза Вонга.
вправо, то есть это тоже клауза Вонга.
2.3.3.  .
.
Эту клаузу разбиваем аналогично клаузе 2.2.3.
2.3.3.1.  , 2.3.3.2.
, 2.3.3.2. 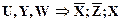 .
.
Клауза 2.3.3.1 уже соответствует клаузе Вонга, в ней 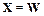 , а клаузу 2.3.3.2 сначала также преобразуем, перенеся из правой части
, а клаузу 2.3.3.2 сначала также преобразуем, перенеся из правой части  в левую с отрицанием, и получим клаузу
в левую с отрицанием, и получим клаузу  , имеющую вид клаузы Вонга, в которой
, имеющую вид клаузы Вонга, в которой  .
.
Таким образом, нами доказана исходная клауза, то есть то, что она записана верно.
6. 1.6. Метод натурального исчисления
Недостатком метода Вонга, как и метода резолюций, является то, что исходная клауза обязательно должна иметь нормальную дизъюнктивную или конъюнктивную форму. Этот недостаток исключен в методе натурального исчисления.
Метод натурального исчисления – метод, в котором процедура доказательства сводится к упорядоченной цепи преобразований, связанных с удалением или введением логических связок на основе десяти правил.
1. Правило введения конъюнкции (ВК)
 ).
).
2. Правило удаления конъюнкции (УК)
 .
.
3. Правило введения импликации (ВИ)
 ,
,  .
.
4. Правило удаления импликации (УИ)
 .
.
5. Правило введения дизъюнкции (ВД)
 .
.
6. Правило удаления дизъюнкции (УД)
 .
.
7. Правило введения отрицания (ВО)
 .
.
8. Правило удаления отрицания (УО)
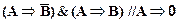 .
.
9. Правило введения эквивалентности (ВЭ)
 .
.
10. Правило удаления эквивалентности (УЭ)
 .
.
Эти правила надо понимать так: если слева от символа «//» стоят истинные клаузы, то справа от символа «//» тоже будут стоять истинные клаузы. Например, первое правило введения конъюнкции можно прочитать следующим образом: если высказывания А и В (связка «и» передается знаком «&») порознь истинные (о чем говорят рядом стоящие с этими буквами символы метаимпликации « »), то будет истинной и их конъюнкция
»), то будет истинной и их конъюнкция  . При этом надо помнить, что во всех десяти правилах перед символом метаимпликации «
. При этом надо помнить, что во всех десяти правилах перед символом метаимпликации « » может стоять любой перечень посылок Р. Так, десятое правило может выглядеть следующим образом:
» может стоять любой перечень посылок Р. Так, десятое правило может выглядеть следующим образом:
 .
.
Кроме перечисленных десяти правил, имеется еще одно – базовое правило (БП), которое сначала сформулируем словами: во-первых, любая посылка может выступать в роли следствия, то есть
 ,
,  ,
, 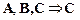
будут всегда истинными и не требуют доказательства, так как удовлетворяют аксиоме порядка; во-вторых, в перечень посылок истинной клаузы всегда можно добавить новые посылки, то есть если клауза
|
|
|
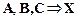
верна, то будут истинными и все клаузы, построенные на ее основе
 ,
,  .
.
В обобщенной форме базовое правило можно записать так:
 ,
,
где  - любая посылка из Р, а
- любая посылка из Р, а 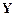 - произвольная посылка.
- произвольная посылка.
Рассмотрим следующую клаузу, представляющую собой тавтологию
 .
.
Доказать справедливость этой клаузы.
1.  (УИ)
(УИ)
2.  (УИ)
(УИ)
3.  (1, БП)
(1, БП)
4.  (2, БП)
(2, БП)
5. 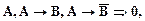 (3,4,УО)
(3,4,УО)
6. 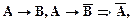 (5, ВО)
(5, ВО)
7.  (6, ВИ)
(6, ВИ)
8.  . (7, ВИ)
. (7, ВИ)
Справа в круглых скобках указаны номер строки, из которой получена данная клауза, а также начальные буквы используемого правила.
Доказать клаузу
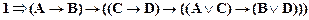 .
.
1.  (УИ)
(УИ)
2.  (1, УИ)
(1, УИ)
3.  (2, УИ)
(2, УИ)
4.  (3)
(3)
5. 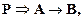 (Р1, БП)
(Р1, БП)
6.  (5, УИ)
(5, УИ)
7.  (6,ВД)
(6,ВД)
8. 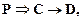 (Р2, БП)
(Р2, БП)
9.  (8, УИ)
(8, УИ)
10.  (6, ВД)
(6, ВД)
11.  (Р2, БП)
(Р2, БП)
12.  (7,10,11, УД)
(7,10,11, УД)
Каждую клаузу в нижеприведенных вариантах необходимо доказать следующими методами: аксиоматическим, натурального исчисления, резолюций и Вонга.
1.  ,
,
 ,
,
 .
.
2.  ,
,
 ,
,
 .
.
3.  ,
,
 ,
,
 .
.
4.  ,
,
 ,
,
 .
.
5.  ,
,
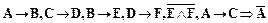 ,
,
 .
.
6.  ,
,
 ,
,
 .
.
7.  ,
,
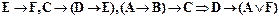 ,
,
 .
.
8.  ,
,
 ,
,
 .
.
9.  ,
,
 ,
,
 .
.
10.  ,
,
 ,
,
 .
.
11. 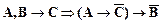 ,
,
 ,
,
 .
.
12.  ,
,
 ,
,
 .
.
13. 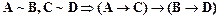 ,
,
 ,
,
 .
.
14.  ,
,
 ,
,
 .
.
15.  ,
,
 ,
,
 .
.
16.  ,
,
 ,
,
 .
.
17.  ,
,
 ,
,
 .
.
18.  ,
,
 ,
,
 .
.
19. 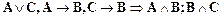 ,
,
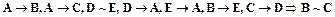 ,
,
 .
.
20.  ,
,
 ,
,
 .
.
21.  ,
,
 ,
,
 .
.
22.  ,
,
 ,
,
 .
.
23.  ,
,
 ,
,
 .
.
24.  ,
,
 ,
,
 .
.
1. В чем заключается различие в построении доказательств в логике высказываний и логике Буля?
2. Какие символы используются для построения доказательств в алгебре высказываний?
3. Записать причинно-следственное отношение, которое используется для доказательства какого-либо утверждения.
4. Дать определение клаузы. Записать законы рефлексивности, антисимметричности и транзитивности для отношения порядка.
5. Дать определение легенды. Привести пример.
6. Привести запись тавтологии и противоречия.
7. Привести пять методов доказательств справедливости логических клауз.
8. В чем заключается аксиоматический метод доказательства логических выражений. Доказать справедливость клаузы modus ponens – правила отделения.
9. На чем основан конструктивный метод доказательства логических выражений. В каком случае клауза считается истинной?
|
|
|
10. Что такое минимальное и трансверальное покрытие?
11. В чем заключается принцип резолюций? Пример.
12. На чем основывается метод Вонга?
13. Преимущество метода натурального исчисления. Десять правил метода натурального исчисления.
1. Акимов, О. Е. Дискретная математика. Логика, группы, графы / О. Е. Акимов. – М.: Лаборатория базовых знаний, 2001.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 165; Нарушение авторских прав?; Мы поможем в написании вашей работы!