
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные свойства определенных интегралов
|
|
|
|
 Наиболее просто и естественно установить эти свойства, опираясь на какой-либо наглядный смысл определенного интеграла. Например, на то, что любой определенный интеграл
Наиболее просто и естественно установить эти свойства, опираясь на какой-либо наглядный смысл определенного интеграла. Например, на то, что любой определенный интеграл  связан, согласно (3), (5) и (6), с площадями криволинейных трапеций. Но использовать этот геометрический смысл определенного интеграла для вывода его свойств в самом общем случае, то есть в случае знакопеременной функции y = f(x), не очень удобно. Гораздо удобнее и нагляднее установить эти свойства, если, в соответствии с (12), считать определенный интеграл
связан, согласно (3), (5) и (6), с площадями криволинейных трапеций. Но использовать этот геометрический смысл определенного интеграла для вывода его свойств в самом общем случае, то есть в случае знакопеременной функции y = f(x), не очень удобно. Гораздо удобнее и нагляднее установить эти свойства, если, в соответствии с (12), считать определенный интеграл  работой А силы f(x) (силы любого направления, а значит, и любого знака), когда точка приложения х этой силы перемещается вдоль оси ох из положения а в положение b (рис. 10).
работой А силы f(x) (силы любого направления, а значит, и любого знака), когда точка приложения х этой силы перемещается вдоль оси ох из положения а в положение b (рис. 10).
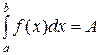 (22)
(22)
Тогда сразу становятся очевидными следующие
Свойства определенных интегралов:
1) 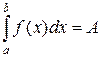 – число – число
| (23) |
(число А может быть любого знака).
2) 
| (24) |
(переменную интегрирования в определенном интеграле можно обозначить как угодно – результат не изменится).
3) 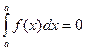
| (25) |
(ибо если перемещение точки отсутствует, то работа любой силы f(x) равна нулю).
4) 
| (26) |
(ибо если сила отсутствует, то и работа отсутствует).
5) 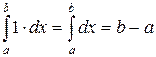
| (27) |
(ибо работа постоянной единичной силы численно равна перемещению точки под действием этой силы).
6) 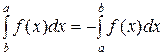
| (28) |
7) Для любых трех чисел a,b и c (при всех возможных их расположениях относительно друг друга, см рисунки ниже) справедливо равенство

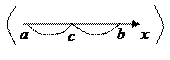
 |
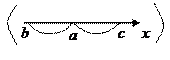
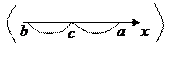
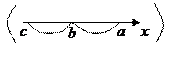
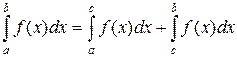
| (29) |
8) 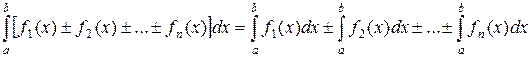 (30) (30)
|
9) 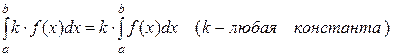
| (31) |
10) Если f(x) ≤ g(x) для всех x Î[ a; b ], то 
| (32) |
(физический смысл последних пяти свойств продумать самостоятельно).
11) Пусть m = [ f(x) ] наим и М = [ f(x) ] наиб – соответственно наименьшее и наибольшее значения функции f(x) на промежутке [ a; b ]. Тогда
|
|
|
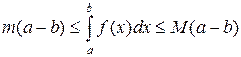
| (33) |
Действительно, так как m ≤ f(x)≤ M для всех xÎ [ a; b ], то применяя свойство (32) и затем свойства (31) и (27), мы и получим двойное неравенство (33). Это неравенство часто используется для прикидки (грубой оценки) величины  .
.
12) (теорема о среднем). Если функция f(x) непрерывна на отрезке [ a; b ], то на этом отрезке найдется такая точка  , что справедливо следующее равенство:
, что справедливо следующее равенство:

| (34) |
Пример 1. Оценить величину  .
.
Решение. Так как функция 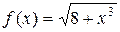 монотонно возрастает на отрезке [1; 3], то
монотонно возрастает на отрезке [1; 3], то 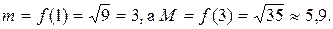 Поэтому по формуле грубой оценки (33) получаем:
Поэтому по формуле грубой оценки (33) получаем:
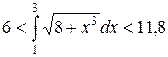
Пример 2. Оценить величину 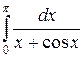 .
.
Решение. Минимальное m и максимальное M значения функции  на промежутке [0; p] не очевидны, так как с возрастанием х в выражении x + cos x первое слагаемое растет, а второе убывает. Чтобы разобраться в поведении функции y, найдем ее производную:
на промежутке [0; p] не очевидны, так как с возрастанием х в выражении x + cos x первое слагаемое растет, а второе убывает. Чтобы разобраться в поведении функции y, найдем ее производную:
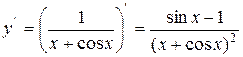 .
.
Так как sin x ≤ 1 для всех х, то 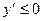 для всех х. А значит, функция
для всех х. А значит, функция  убывает на всей области своего определения, в том числе и на отрезке [0; p]. Таким образом, на отрезке [0; p]
убывает на всей области своего определения, в том числе и на отрезке [0; p]. Таким образом, на отрезке [0; p]

Следовательно, оценка (4.18) для данного интеграла имеет вид:
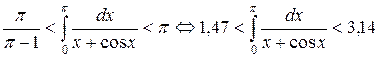
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 258; Нарушение авторских прав?; Мы поможем в написании вашей работы!