Функция . Биномиальный ряд

Функция.

Теорема. Справедливо разложение

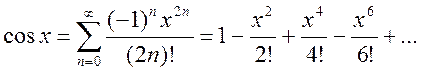
(3)

Доказательство.

Пользуясь свойством почленного дифференцирования абсолютно сходящихся рядов, имеем из формулы (2)

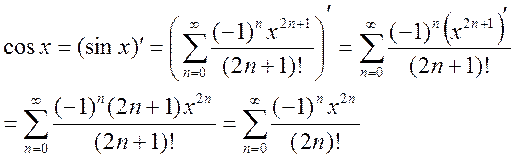
Полученный ряд сходится абсолютно при

Теорема доказана.

Теорема. Справедливо разложение

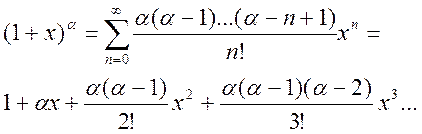
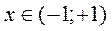(4)

Доказательство.

1) Вычисление коэффициентов Тейлора в точке .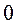

Так как

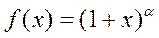
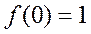
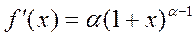
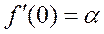
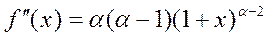
то

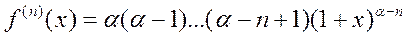
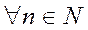
то

.

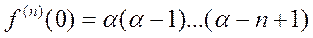Следовательно, коэффициенты ряда Маклорена

2) Ряд Маклорена имеет вид

~

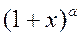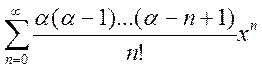
3) Найдем радиус сходимости

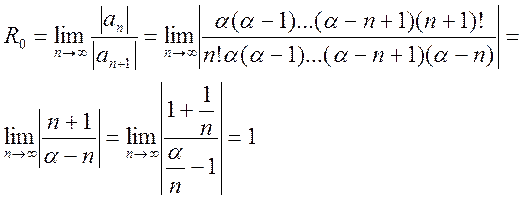
Следовательно, ряд Маклорена сходится абсолютно при всех .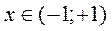

Для доказательства сходимости ряда (4) к исходной функции следует рассматривать остаточный член в форме Пеано, поэтому это доказательство не приводим.

Теорема доказана.

Замечание 1. В точках 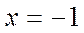и 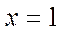сходимость ряда (4) зависит от заданного значения .

Замечание 2. Частные случаи.

− при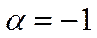

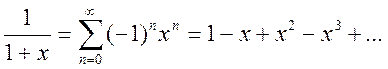
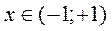(5)

− при

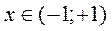
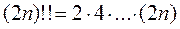
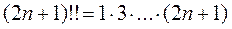
Применим полученную формулу для вычисления .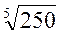

Ищем ближайшую известную 5-ю степень: .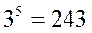

Тогда

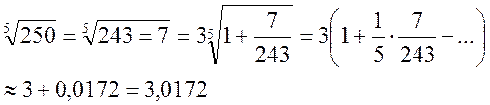
Дата добавления: 2013-12-13