Основные функции распределения

Наиболее полную информацию о случайной величине даёт функция её распределения.

При статистической обработке результатов экспериментов стоит задача подбора теоретических кривых распределения к имеющемуся эмпирическому закону распределения случайной величины.

Пусть в результате п измерений случайной величины получен ряд её значений х₁, х₂, …, х_п. При первичной обработке таких рядов их вначале группируют в интервалы и устанавливают для каждого из них частоты W_i(x_i). По Значениям x_i и W_i строят ступенчатую гистограмму частот (см.рис.3) и определяют характеристики эмпирической кривой распределения: среднеарифметическое значение 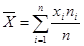, дисперсию 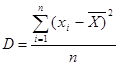и среднее квадратическое отклонение , которые соответствуют значениям этих параметров для теоретических распределений случайной величины.

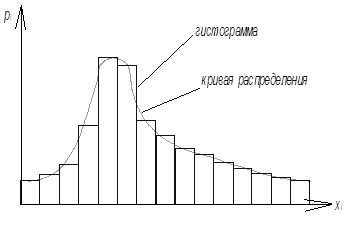
Рис.3 Общий вид распределения случайных величин

При решении задач практики могут иметь место различные виды распределений случайной величины. Рассмотрим только наиболее употребительные виды распределений.

Нормальное распределение (Гаусса). Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

.

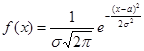Нормальное распределение полностью характеризуется двумя параметрами: а и s. Для задания этого распределения достаточно знать эти два параметра. На рис.4,а представлен общий вид кривой нормального распределения.

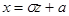Для упрощения математических выражений вводится нормированная величина Þ Þ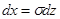. Эти переменные подставляются в формулу математического ожидания и среднего квадратического отклонения, в результате для этого отклонения получается: М(Х)=а, D(X)=s², s(X)=s.

Нормальное распределение с параметрами а=0 и s=1 называется нормированным. Оно описывается уравнением . На рис.4,б показано нормированное распределение. При изменении а (математического ожидания) график смещается вдоль оси Ох, при возрастании s рассеяние увеличивается, максимальная ордината кривой убывает 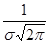, а сама кривая становится более пологой (рис.5). Таким образом, чем меньше s, тем больше сходимость результатов измерений, а ряд измерений более точен, т.е. большинство измерений мало отличается друг от друга. Отклонения ±s соответствуют точкам перегиба кривой (заштрихованная область). Вероятность того, что случайные величины не выйдут за эти пределы составляет 0,683.

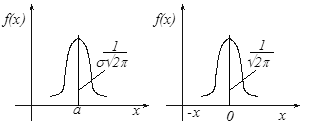
а) б)

рис.4 Общий вид кривой нормального распределения

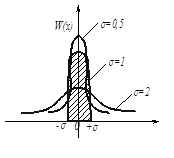
рис.5 Характер рассеивания кривой нормального распределения

Распределение c² (хи-квадрат). Это распределение суммы квадратов независимых случайных величин, подчинённых стандартному нормальному закону распределения.

Обозначим исходные независимые случайные величины буквами Х₁, Х₂, …, Х_n, а сумму их квадратов c_i ², т.е. c_п²= Х₁² +Х₂²+ …+Х_n ².

Число слагаемых в этой формуле п называется числом степеней свободы c_п². Каждая величина в этой формуле Х₁, Х₂, …, Х_n имеет стандартное нормальное распределение. Математическое ожидание величины c_п² равно: М (c_п²)=п. Дисперсия – D (c_п²)=2n.

Распределение c_п² полностью характеризуется одним параметром – числом степеней свободы п. С увеличением степеней свободы распределение медленно приближается к нормальному (рис.6).

Рис.6 Плотность распределения c_п²

2.2.4 Вероятность попадания в заданный интервал нормальной случайной величины. Правило трёх сигм

Вероятность попадания случайной величины в заданный интервал [a, b] можно вычислить по формуле: 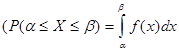. Если случайная величина имеет нормальный закон распределения, то

Путём замены переменной t=(х-а)/s и вычисления интеграла эта формула сводится к виду .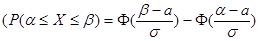

Ф(t)= 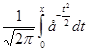– функция Лапласа. Её значения приводятся во всех учебниках по математической статистике. В Exel имеется команда НормРаспред.

Пример: случайная величина Х распределена по нормальному закону. Математическое ожидание равно 30, среднее квадратичное отклонение – 10. Найти вероятность того, что Х примет значение в интервале от 10 до 50. По приведённой выше формуле получим .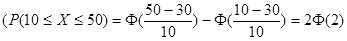

По таблице значений функции Ф(х) находим, что Ф(2)=0,4772, следовательно Р(10≤Х≤50)=2·0,4772=0,9544.

Часто требуется вычислить вероятность того, что отклонение нармально распределённой случайной величины Х по абсолютной величине меньше некоторого заданного положительного числа d, т.е. вычислить вероятность осуществления неравенства |X-a|<d. На основе рассмотренной выше формулы может быть получено выражение: P(|X-a|<d)=2Ф(d/s).

Пример: случайная величина Х распределена по нормальному закону. Математическое ожидание равно 20, среднее квадратичное отклонение – 10. Найти вероятность того, что отклонение по абсолютной величине будет не больше 3. По приведённой формуле будем иметь: P(|X-20|<3)=2Ф(3/10), Ф(0,3)=0,1179. Следовательно, P(|X-20|<3)=2·0,1179=0,2358.

Выполним в последней расчётной формуле замену d=st. Она примет вид
P(|X-a|<st)=2Ф(t).

Зададим t=3, тогда P(|X-a|<3s)=2Ф(3)=2·0,49865=0,9973. Это соотношение означает, что событие, состоящее в осуществлении неравенства |X-a|<3s, имеет вероятность близкую к 1, значит оно почти достоверно.

Формула P(|X-a|<3s)=2Ф(3)=2·0,49865=0,9973 выражает так называемое правило трёх сигм.

Правило трёх сигм: если случайная величина распределена по нормальному закону, то модуль её отклонения от математического ожидания не превосходит утроенного среднеквадратичного отклонения.

Дата добавления: 2014-01-04