
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
RB-властивості. Бінарне дерево називається червоно-чорним, якщо воно має наступні властивості:
|
|
|
|
Бінарне дерево називається червоно-чорним, якщо воно має наступні властивості:
1) кожна вершина або червона, або чорна,
2) корінь дерева – чорний,
3) кожний листок (NULL) – чорний,
4) якщо вершина червона, обидві його нащадки чорні,
5) усі шляхи від кореня до листків, мають однакову кількість чорних вершин.
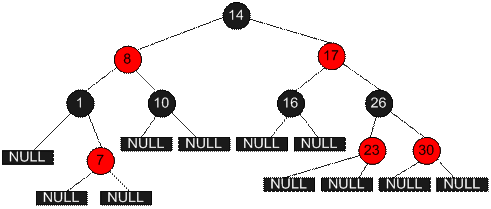
Такі властивості надають червоно-чорному дереву додаткового обмеження: найдовший шлях із кореня до будь-якого листка перевищує найкоротший шлях не більше ніж вдвічі. У цьому сенсі таке дерево можна назвати збалансованим. Зважаючи на те, що час виконання основних операцій з бінарними деревами пошуку залежить від висоти, таке обмеження ґарантує їхню ефективність в найгіршому випадку, чого звичайні бінарні дерева ґарантувати не можуть.
Для того, щоби зрозуміти, чому перелічені властивості забезпечують існування такого обмеження, зазначимо, що в червоно-чорному дереві, відповідно до властивості 4, не існує такого шляху, на якому б зустрілися дві червоні вершини підряд. Найкоротший шлях складається з усіх чорних вершин, а в найдовшому червоні та чорні вершини чергуються. З врахуванням властивості 5, отримуємо, що глибина будь-яких двох листів відрізняється не більше ніж в два рази.
У деяких зображеннях червоно-чорних дерев, NULL-листки не наводяться, тому що вони не містять корисної інформації, але їхнє існування необхідне для забезпечення усіх властивостей.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 620; Нарушение авторских прав?; Мы поможем в написании вашей работы!