
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Смешанное произведение трех векторов
|
|
|
|
Определение 3.19.1. Смешанным произведением трех векторов 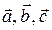 называется число
называется число
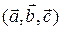 =
= 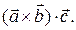 (3.19.1)
(3.19.1)
Из определения ясно, что если хотя бы один из данных векторов нулевой, то смешанное произведение, очевидно, равно нулю. Больше того, когда два из них коллинеарны, например,  , то по определению векторного произведения
, то по определению векторного произведения 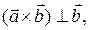 следовательно,
следовательно, 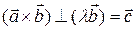 , отсюда
, отсюда 
Теорема 3.19.1. Необходимым и достаточным условием компланарности трех векторов 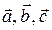 является равенство нулю их смешанного произведения, т. е.
является равенство нулю их смешанного произведения, т. е. 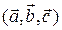 = 0.
= 0.
Доказательство. Необходимость. Если векторы 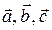 компланарны, то вектор
компланарны, то вектор 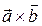 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов  и
и 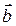 , а, следовательно, он перпендикулярен вектору
, а, следовательно, он перпендикулярен вектору  , поэтому
, поэтому  .
.
Достаточность. Пусть  = 0. Будем считать, что среди данных векторов нет нулевого, а также никакие два из них не являются коллинеарными, ибо иначе сразу можно утверждать, что векторы
= 0. Будем считать, что среди данных векторов нет нулевого, а также никакие два из них не являются коллинеарными, ибо иначе сразу можно утверждать, что векторы 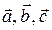 компланарны.
компланарны.
Тогда
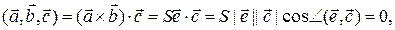
откуда  , следовательно, вектор
, следовательно, вектор  лежит в плоскости векторов
лежит в плоскости векторов  ,
,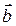 , т. е. векторы
, т. е. векторы 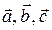 компланарны.
компланарны.
Теорема 3.19.2. Смешанное произведение трех векторов 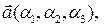
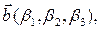
 заданных своими аффинными координатами, вычисляется по формуле
заданных своими аффинными координатами, вычисляется по формуле
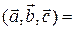
 (3.19.2)
(3.19.2)
Доказательство. Формула (3.19.2) следует из формулы (3.18.1) и (3.16.3).
Следствие 3.19.1. Смешанное произведение трех векторов 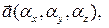
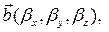
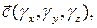 заданных своими декартовыми координатами, находится по формуле
заданных своими декартовыми координатами, находится по формуле
 =
= –
–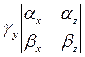 +
+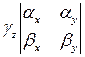
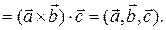
Теорема 3.19.3. Смешанное произведение  трех некомпланарных векторов равно объему параллелепипеда, построенного на векторах-сомножителях после приведения их в общее начало, взятому со знаком “+”, если тройка
трех некомпланарных векторов равно объему параллелепипеда, построенного на векторах-сомножителях после приведения их в общее начало, взятому со знаком “+”, если тройка 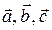 правая, и со знаком “–”, если эта тройка левая.
правая, и со знаком “–”, если эта тройка левая.
Доказательство. Пусть S — площадь параллелограмма, построенного на векторах  и
и 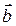 после приведения их в общее начало. Допустим, что
после приведения их в общее начало. Допустим, что 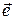 — орт вектора
— орт вектора 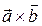 , а h — высота параллелепипеда, построенного на векторах
, а h — высота параллелепипеда, построенного на векторах 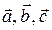 , при условии, что основанием служит параллелограмм, построенный на векторах
, при условии, что основанием служит параллелограмм, построенный на векторах  и
и 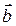 (рис. 3.19.1, 3.19.2).
(рис. 3.19.1, 3.19.2).
|
|
|
 Рис. 3.19.1
Рис. 3.19.1
| 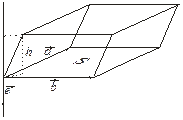 Рис. 3.19.2
Рис. 3.19.2
|
Ясно, что 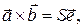
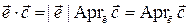 . Отметим, что
. Отметим, что  , если тройка векторов
, если тройка векторов 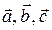 является правой, и
является правой, и  , если — левой.
, если — левой.
Тогда
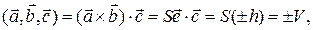
где V объем параллелепипеда, причем берем “+”, если тройка 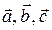 правая, и “–”, если эта тройка — левая.
правая, и “–”, если эта тройка — левая.
Следствие 3.19.2. Верно равенство
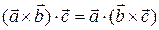 . (3.19.3)
. (3.19.3)
Доказательство. В самом деле, в силу коммутативности скалярного произведения 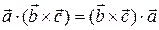 , поэтому достаточно показать, что
, поэтому достаточно показать, что 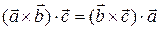 . Последнее равенство очевидно, ибо абсолютная величина каждого из чисел равна объему параллелепипеда, построенного на векторах
. Последнее равенство очевидно, ибо абсолютная величина каждого из чисел равна объему параллелепипеда, построенного на векторах 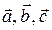 , исходящих из общей точки, и, кроме того, эти числа имеют одинаковые знаки, так как тройки векторов
, исходящих из общей точки, и, кроме того, эти числа имеют одинаковые знаки, так как тройки векторов 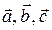 и
и  имеют одинаковую ориентацию.
имеют одинаковую ориентацию.
Из теоремы 3.19.3 следует, что (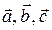 ) > 0 ((
) > 0 ((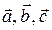 ) <0), когда тройка векторов
) <0), когда тройка векторов 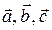 — правая (левая). Поэтому правую (левую) тройку векторов иногда называют положительно (отрицательно) ориентированной.
— правая (левая). Поэтому правую (левую) тройку векторов иногда называют положительно (отрицательно) ориентированной.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 718; Нарушение авторских прав?; Мы поможем в написании вашей работы!