Функциональный уровень проектирования аналоговых устройств

На функционально-логическом уровне исследуют устройства, в качестве элементов которых принимают достаточно сложные узлы и блоки, считавшиеся системами на макроуровне. Поэтому необходимо упростить представление моделей этих узлов и блоков по сравнению с их представлением на макроуровне. Другими словами, вместо полных моделей узлов и блоков нужно использовать их макромодели.

Вместо двух типов фазовых переменных в моделях функционально-логического уровня фигурируют переменные одного типа, называемые сигналами. Физический смысл сигнала, т.е. его отнесение к фазовым переменным типа потока или типа потенциала, конкретизируют в каждом случае исходя из особенностей задачи.

Основой моделирования аналоговых устройств на функционально-логическом уровне является использование аппарата передаточных функций. При этом модель каждого элемента представляют в виде уравнения вход-выход, т.е. в виде

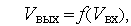
(1)

где 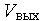и 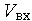— сигналы на выходе и входе узла соответственно. Если узел имеет более чем один вход и один выход, то в (1) скаляры 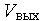и 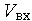становятся векторами. Однако известно, что представление модели в виде (1) возможно только, если узел является безынерционным, т.е. в полной модели узла не фигурируют производные.

Следовательно, для получения (1) в общем случае требуется предварительная алгебраизация полной модели. Такую алгебраизацию выполняют с помощью преобразования Лапласа, переходя из временной области в пространство комплексной переменной .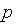

Тогда в моделях типа (1) имеют место не оригиналы, а изображения сигналов 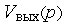и 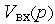. Сами же модели реальных блоков стараются по возможности максимально упростить и представить их моделями типовых блоков (звеньев) из числа заранее разработанных библиотечных моделей. Обычно модели звеньев имеют в пространстве изображений вид

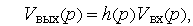
где 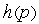— передаточная функция звена.

В случае применения преобразования Лапласа появляются ограничения на использование нелинейных моделей, а именно: в моделях не должно быть нелинейных инерционных элементов. Другое упрощающее допущение при моделировании на функционально-логическом уровне — неучет влияния нагрузки на характеристики блоков. Действительно, подключение к выходу блока некоторого другого узла никак не влияет на модель блока рис.1.

Собственно получение ММС из ММЭ оказывается вследствие принятых допущений значительно проще, чем на макроуровне: ММС есть совокупность ММЭ, в которых отождествлены сигналы на соединенных входах и выходах элементов. Эта ММС представляет собой систему алгебраических уравнений.

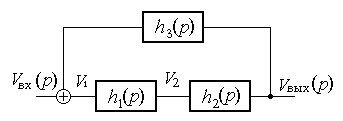
Получение ММС проиллюстрируем простым примером (см. рис. 1), где показана система из трех блоков с передаточными функциям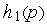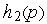и , и . ММС имеет вид:



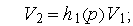
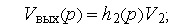
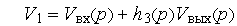
или

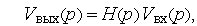
где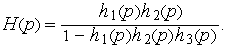

Рис. 1. Пример математической модели на функциональном уровне

Таким образом, анализ сводится к следующим операциям:

1. заданную схему устройства представляют совокупностью звеньев и, если схема не полностью покрывается типовыми звеньями, то разрабатывают оригинальные модели;

2. формируют ММС из моделей звеньев;

3. применяют прямое преобразование Лапласа к входным сигналам;

4. решают систему уравнений ММС и находят изображения выходных сигналов;

5. с помощью обратного преобразования Лапласа возвращаются во временную область из области комплексной переменной .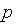

Преобразования Лапласа. Исследование существенно упрощается при использовании прикладных математических методов операционного исчисления. Преобразование Лапласа устанавливает взаимно однозначное соответствие между исходной функцией времени f(t) и другой функцией другой (комплексной) переменной F(p). Например, функционирование некоторой системы описывается ДУ вида

(2.1)

где х и у - входная и выходная величины. Если в данное уравнение вместо x(t) и y(t) подставить функции X(s) и Y(s) комплексного переменного s такие, что

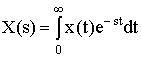
и

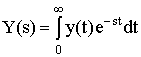
(2.2)

то исходное ДУ при нулевых начальных условиях равносильно линейному алгебраическому уравнению

a₂ s² Y(s) + a₁ s Y(s) + a₀ Y(s) = b₁ X(s) + b₀ X(s).

Такой переход от ДУ к алгебраическому уравнению называется преобразованием Лапласа, формулы (2.2) соответственно формулами преобразования Лапласа, а полученное уравнение - операторным уравнением.

Новые функции X(s) и Y(s) называются изображениями x(t) и y(t) по Лапласу, тогда как x(t) и y(t) являются оригиналами по отношению к X(s) и Y(s).

Переход от одной модели к другой достаточно прост и заключается в замене знаков дифференциалов 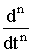на операторы sⁿ, знаков интегралов на множители 1/s, а самих x(t) и y(t) - изображениями X(s) и Y(s).

Для обратного перехода от операторного уравнения к функциям от времени используется метод обратного преобразования Лапласа. Общая формула обратного преобразования Лапласа:

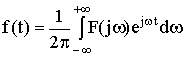(2.3)

где f(t) - оригинал, F(j) - изображение при s = j, j - мнимая единица,  - частота.

Эта формула достаточно сложна, поэтому были разработаны специальные таблицы, в которые сведены наиболее часто встречающиеся функции F(s) и их оригиналы f(t). Они позволяют отказаться от прямого использования формулы (2.3).

Примеры типовых звеньев. Звеном системы называется ее элемент, обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь разную физическую основу (электрические, пневматические, механические и др. звенья), но относится к одной группе. Соотношение входных и выходных сигналов в звеньях одной группы описываются одинаковыми передаточными функциями.

Простейшие типовые звенья:

 усилительное,

 интегрирующее,

 дифференцирующее,

 апериодическое,

 колебательное,

 запаздывающее.

1) Усилительное звено

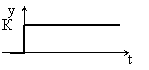Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления. Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз. Примерами таких звеньев являются: механические передачи, датчики, безынерционные усилители и др.

2) Интегрирующее.

2.1) Идеальное интегрирующее.

Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины

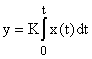W(s)=

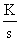
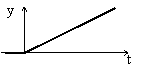
При подаче на вход звена воздействия выходной сигнал постоянно возрастает. Это звено астатическое, т.е. не имеет установившегося режима.

2.2) Реальное интегрирующее

. Передаточная функция этого звена имеет вид: W(s) = .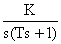

Переходная характеристика в отличие от идеального звена является кривой. Примером интегрирующего звена является двигатель постоянного тока с независимым возбуждением, если в качестве входного воздействия принять напряжение питания статора, а выходного - угол поворота ротора.

3) Дифференцирующее.

3.1) Идеальное дифференцирующее. Выходная величина пропорциональна производной по времени от входной:

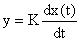; W(s) = K*s

При ступенчатом входном сигнале выходной сигнал представляет собой (дельта-функцию).

3.2) Реальное дифференцирующее.

Идеальные дифференцирующие звенья физически не реализуемы. Большинство объектов, которые представляют собой дифференцирующие звенья, относятся к реальным дифференцирующим звеньям. Переходная характеристика и передаточная функция этого звена имеют вид:

W(s) = .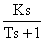

4) Апериодическое (инерционное).

Этому звену соответствует ДУ вида:

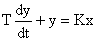
; W(s) = .

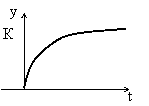y(t)=Kx₀₍1-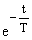) Постоянная Т называется постоянной времени. Большинство тепловых объектов являются апериодическими звеньями. Например, при подаче на вход электрической печи напряжения ее температура будет изменяться по аналогичному закону.

5) Колебательное звено имеет ДУ вида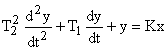

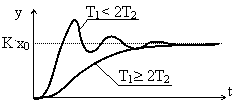
W(s)=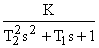 При подаче на вход ступенчатого воздействия амплитудой х₀ на переходная кривая будет иметь один из двух видов: апериодический (при Т₁ > 2Т₂) или колебательный (при Т₁ < 2Т₂).

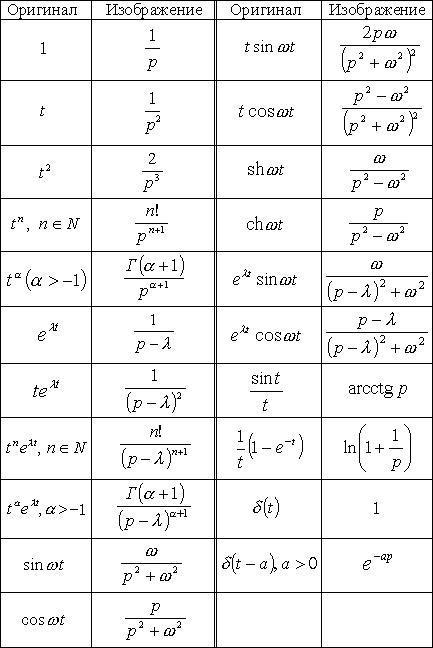
Таблицаосновных преобразований Лапласа

Дата добавления: 2014-01-05