Способы описания случайных процессов.

Существуют два способа представления случайных процессов.

1. Случайный процесс представляется в виде совокупности или ансамбля всех своих возможных реализаций. То, какая конкретно реализация будет наблюдаться в испытании, является случайным событием. На рис. 1,а показан случайный процесс £(t), в ансамбль которого входят три реализации x₁(t)_, x₂(t), x₃(t), наблюдаемые в испытании с определенными вероятностями.

2. Случайный процесс 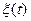рассматривается как n-мерная случайная величина или n-мерный вектор (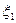,,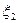...,), каждая проекция которого является отсчетом случайного процесса в моменты времени t₁, t₂,..., t (рис. 1,б). Эти проекции вектора или отсчеты процесса будем называть сечениями случайного процесса:

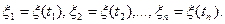(2.1)

Сечения (1.1) являются случайными величинами, так как из-за случайного выбора реализации их конкретные значения до опыта неизвестны. На рис. 1. пунктиром показан возможный ход случайного процесса и соответственно случайные величины 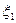,,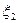...,на осях возможных значений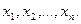

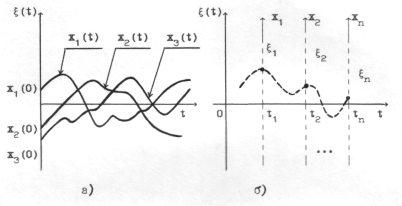
Рис. 1

При достаточно большом п задание процесса n-мерным вектором эквивалентно заданию самого процесса. В теории случайных процессов доказывается, что для используемых на практике процессов число n конечно. Этот вывод базируется на том, что реализации случайного процесса имеют ограниченную ширину спектра.

Представление случайного процесса n-мерным вектором позволяет свести вероятностное описание процесса к описанию n-мерной случайной величины. Рассмотрим функцию распределения, плотность вероятности и числовые характеристики непрерывного случайного процесса, представленного n-мерным вектором.

В соответствии с этим n-мерая функция распределения случайного процесса определится выражением

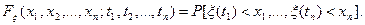(2.2)

Выражение (2.2) показывает, что в общем случае 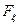зависит от 2n аргументов: от n наперед заданных возможных значений сечений (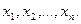) и от п моментов времени (t₁, t₂,..., t), в которых эти сечения берутся. Вероятностный смысл выражения (2.2) поясняется рис. 3,а. для n=3: функция 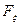определяет вероятность того, что реализация случайного процесса 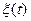пройдет ниже заданных значений 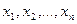в моменты времени t₁, t₂,..., t.

Многомерная плотность вероятности по определению равна частной производной n-го порядка от 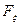по возможным значениям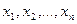

(2.3)

Плотность вероятности n-го порядка в общем случае также зависит от тех же 2n аргументов. Вероятностный смысл выражения (2.3) поясняется рис. 2б, для n=3. Плотность вероятности умноженная на dz₁,dz₂,dz₃, определяет вероятность прохождения реализации x(t) процесса 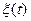через dx₁, dx₂, dx₃, находящихся в сечениях t₁, t₂, t₃ у значений x₁, x₂, x₃.

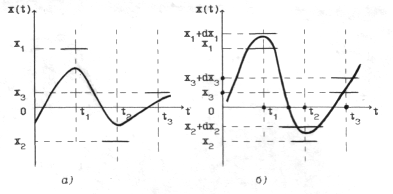
Рис. 2

Произведение двумерной плотности вероятности на dx₁dx₂ 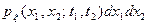характеризует вероятность того, что реализация x(t) случайного процесса в моменты времени t₁, t₂ пройдет через интервалы 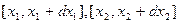. Это означает, что двумерная плотность вероятности содержит сведения о связи между двумя сечениями случайного процесса, проведенными в моменты t_j и t₂.

Одномерная плотность вероятности 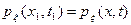, где х₁=х, t₁=t определяет закон распределения случайной величины, полученной в результате сечения случайного процесса в момент t₁=t. Индекс 1 у времени и возможного значения здесь опускается, потому что сечение одно и надобность в индексе отпадает.

Следует также указать, что все свойства функции распределения и плотности вероятности, раскрытые для двумерной случайной величины, распространяются и на случайный процесс, представляемый n-мерной величиной.

Представление случайного процесса n-мерным вектором позволяет получить такие числовые характеристики случайного процесса, как математическое ожидание, дисперсия, корреляционная функция. Эти характеристики, являющиеся соответственно начальными моментами первого порядка, центральным моментом второго порядка, смешанным центральным моментом второго порядка, зависят от момента времени, в котором берутся сечения случайного процесса, и поэтому являются моментными функциями времени.

Математическое ожидание 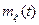и дисперсия 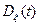требуют для своего определения использование одномерной плотности вероятности::

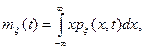(2.4)

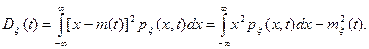(2. 5)

Для определения корреляционной функции требуется использование двумерной плотности вероятности

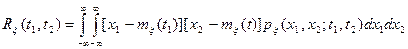(2.6)

не изменится, если все отсчеты времени сместить на одну и ту же величину:

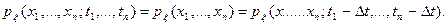(2.7)

Если выбрать 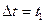, то n-мерная плотность вероятности не будет зависеть от начала отсчета времени

(2.8)

Таким образом, для стационарного процесса одномерная плот­ность вероятности вообще не зависит от времени, а двумерная плот­ность зависит не в отдельности от t₁ и t₂, а от их разности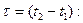

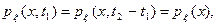(2.9)

(2.10)

В свою очередь, из выражения (1.9) и (1.10) вытекает, что математическое ожидание и дисперсия стационарного процесса не за висят от времени, а корреляционная функция зависит от :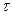

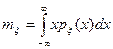(2.11)

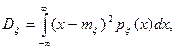(2.12)

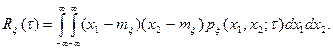(2.13)

Из (2.11), (2.12) и (2.13) следует, что математическое ожидание 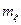постоянно и поэтому для стационарного процесса характеризует постоянную составляющую процесса; постоянность 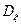характеризует то, что в каждой точке времени t средняя удельная мощность флюктуации (то есть мощность переменной составляющей) одна и та же; зависимость 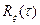от 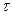означает, что для стационарного процесса не важно, в каких точках t₁ и t₂ берутся сечения, важна разность между ними .

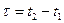Если условие (2.7) не выполняется, то случайный процесс называется нестационарным. Иногда о стационарности судят только по выполнению равенств (2.9), (2.10) и, соответственно, (2.11), (2.12), (2.13). Говорят, что, если выполняются равенства (2.9) и (2.10), то процесс является стационарным, не интересуясь при этом, выполняется условие (2.7) или нет. Такой подход дает более широкое толкование стационарности.

Дата добавления: 2014-01-05