
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Критерий Михайлова. Характеристическое уравнение имеет n корней, которые могут быть действительными, мнимыми и комплексными
|
|
|
|
Характеристическое уравнение имеет n корней, которые могут быть действительными, мнимыми и комплексными. Некоторые из n корней могут оказаться равными между собой (кратными). Комплексные корни всегда попарно сопряженные, при нечетном n имеется хотя бы один действительный корень [6].
Как уже отмечалось, для того чтобы система была устойчивой необходимо, чтобы действительные части всех корней были отрицательными, то есть, чтобы все корни характеристического уравнения лежали левее мнимой оси плоскости комплексного переменного l.
D(l) - характеристический многочлен линейной системы n-ного порядка с положительными коэффициентами. Произведя подстановку l=jw, получим
D(jw)=X(w)+jY(w),
X(w) - четная функция w, Y(w) - нечетная функция w.
Формулировка критерия устойчивости Михайлова [1]:
Для устойчивости линейной системы n-ного порядка необходимо и достаточно, чтобы изменение аргумента функции D(jw) при изменении w от 0 до ¥ равнялось бы np/2, то есть
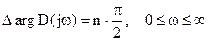 .
.
Доказательство [5].
Пусть li (i =1, 2,.., n) - корни уравнения D(jw)=0. Тогда можно записать
D(jw)=a0(jw-l1)×(jw-l2).. (jw-ln),
½D(jw)½=a0½jw-l1½×½jw-l2½× … ×½jw-ln½,
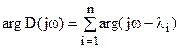 .
.
Покажем, что при изменении w от w=0 до w=¥ каждый отрицательный действительный корень дает приращение аргумента +p/2, а каждая пара комплексных корней - приращение аргумента +p.

Напомним, что разность двух векторов - это вектор, соединяющий их концы, направленный к уменьшаемому вектору.
На рис.2a действительный корень l1 =a1, причем a1<0. При возрастании w от нуля до бесконечности аргумент разности векторов jw-l1 (угол j1 ) изменяется от нуля (при w=0) до +p/2 (положительное направление отсчета углов - против часовой стрелки). На рис.2b корень l2=a2 причем a2>0. При возрастании w от нуля до бесконечности аргумент разности векторов jw-l2 изменяется от нуля (при w=0) до минус p/2.
|
|
|
На рис.3 представлен случай, когда два сопряженных корня имеют отрицательные действительные части.
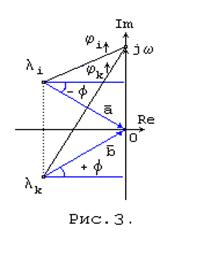
При w=0 углы поворота векторов 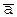 и
и  равны -f и +f, соответственно. При w®¥ угол поворота вектора
равны -f и +f, соответственно. При w®¥ угол поворота вектора  составит p/2+f, а угол поворота вектора
составит p/2+f, а угол поворота вектора  p/2-f, таким образом, суммарное изменение аргумента, вносимое двумя комплексно сопряженными корнями, расположенными в левой полуплоскости l составит угол p.
p/2-f, таким образом, суммарное изменение аргумента, вносимое двумя комплексно сопряженными корнями, расположенными в левой полуплоскости l составит угол p.
Очевидно, что пара комплексно сопряженных корней в правой полуплоскости внесет изменение аргумента равное -p.
Таким образом доказана справедливость критерия Михайлова.
Геометрическая интерпретация критерия.
При изменении w от 0 до +¥ годограф вектора D(jw), начиная с точки, расположенной на положительной части действительной оси, проходит последовательно в положительном направлении n квадрантов. Начало годографа на положительной действительной оси следует из положительности коэффициентов устойчивой системы (необходимое, но недостаточное условие устойчивости).
Если система находится на границе устойчивости (имеются корни вида 0+jw), то годограф пройдет через начало координат. При этом очертания годографа оказываются такими, что малые его деформации в начале координат могут сделать его удовлетворяющим критерию Михайлова.
Если система неустойчива, то малые деформации не могут дать такого эффекта.
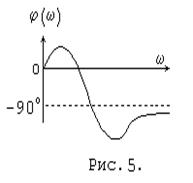
На рис.4 представлены годографы Михайлова для двух астатических систем третьего порядка с постоянными времени T1=0.5c, T2=2c (критический коэффициент усиления Kmax=2.5) для K=2 и K=3 (выше критического). При w®¥ оба годографа асимптотически приближаются к оси абсцисс. При K=2 угол поворота вектора D(jw) равен +270 градусов, при K=3 - угол поворота изменяется не монотонно и при w®¥ оказывается равным минус 90 градусов. На рис.5 представлена качественная зависимость j(w) для K=3.
|
|
|
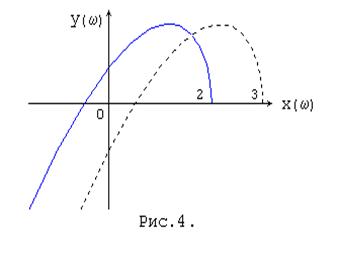
Другая формулировка критерия состоит в том, что корни уравнений X(w)=0 и Y(w)=0, полученных из равенства D(jw)=X(w)+jY(w), должны чередоваться. Первый корень w=0 имеет нечетный многочлен Y(w). Удаленность корней X(w)=0 и Y(w)=0 друг от друга характеризует запас устойчивости САУ.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 793; Нарушение авторских прав?; Мы поможем в написании вашей работы!