
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Бесконечно малые ф-ции
|
|
|
|
Теорема об ограниченности
Свойства предела.
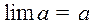 Теорема 1. Предел постоянной = самой постоянной.
Теорема 1. Предел постоянной = самой постоянной.
Теорема 2. Последовательность не может иметь двух различных пределов, если предел существует, то он единственный.
Если функция имеет конечный предел, то она ограничена в окрестности точки а.
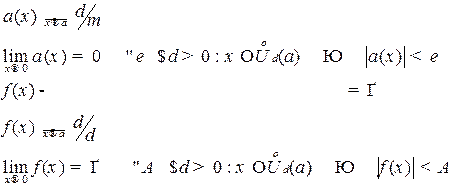 |
бесконечно большой, если ее предел
Св-ва б/м
1.. Сумма б/м есть б/м
2. Произведение б/м ф-ций на ограниченную, есть б/м
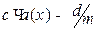 Следствия:
Следствия:
1. произведение б/м на const - б/м:
2. произведение б/м на ф-цию, имеющую предел, - б/м
3. произведение 2-х б/м – б/м:
Теорема 1. критерий существования предела
Понятие непрерывности ф-ции
опр 1: f(x) непрерывна и а, если 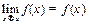
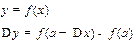
опр 2: f(x) непрерывна и а, если 
Покажем, что это одно и то же:
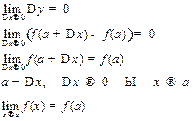
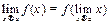 непрерывность означает что предел можно ввести под знак ф-ции.
непрерывность означает что предел можно ввести под знак ф-ции.
 Свойства непрерывности функции:
Свойства непрерывности функции:
1. f(x) непрерывна в а
непрерывны в а
g(x) непрерывна в а
Если ф-ции непрерывны, то их линейные комбинации тоже непрерывны
2. Все элементарные функции непрерывны в каждой точке области их определения
3. f(x) непрерывна в а, g(x) непрерывна в а
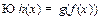 непрерывна в а
непрерывна в а
4. y=f(x) непрерывна в а
 обратная функция
обратная функция 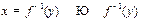 непрерывна в b=f(a)
непрерывна в b=f(a)
I замечательный предел
Теорема. 
Теорема Второй замечательный предел

Производная функции.
Y=f(x) определилась в окрестности U(Xo)
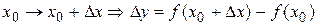
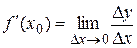 - функция, которая имеет производную, называется дифференцируемой.
- функция, которая имеет производную, называется дифференцируемой.
Теорема: (о непрерывности дифференцируемой функции)
Если функция дифференцируема в Хо, тогда она непрерывна в этой точке.
Док-во:
 , тогда
, тогда 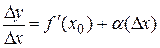


Значение f(x) непрерывно
Y(x) Xо=0, 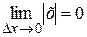 функция непрерывна.
функция непрерывна.
Если 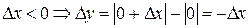 ,
,

 нет предела.
нет предела.
Функция не дифференцируема
Основные формулы дифференцирования.
|
|
|
1. (С)`=0
Док-во: 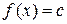

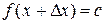
2. 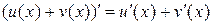 (сложение)
(сложение)
Док-во: 
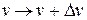
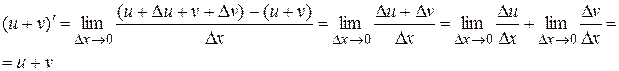
3. 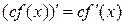
Док-во: 
Производная сохраняет линейные комбинации.
4. Производная произведения:
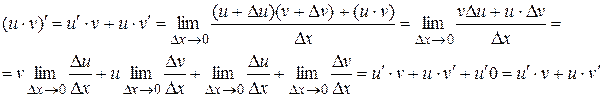
5. Производная частного:

Док-во:
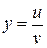

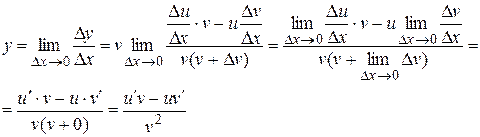
6.Производная сложной функции:

Док-во:
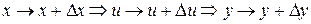
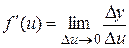
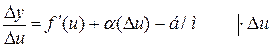
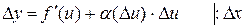
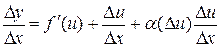

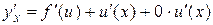
7. Производная обратной функции
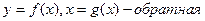
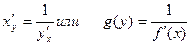
Док-во:
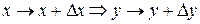
Если 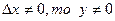
Если 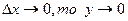
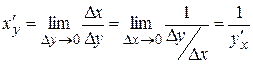
Производные элементарных функций
1. 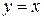 ,
, 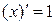
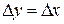
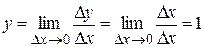
2. 

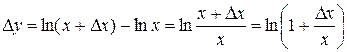
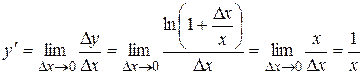
3. 
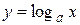
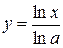
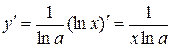
4. 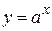 ,
,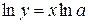 ,
,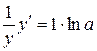
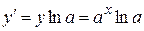
5. 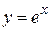
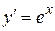
6.  ,
, 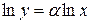
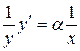

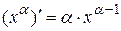
9. 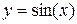

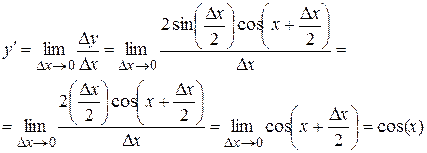
10. 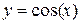
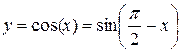
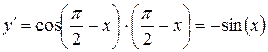
11. 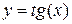
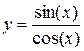
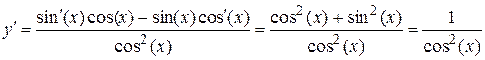
12. 
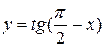

13.
 ,
,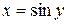
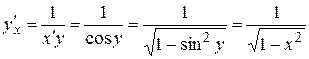
14. 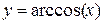 ,
,
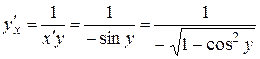
15.  ,
,

16. 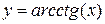 ,
,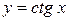
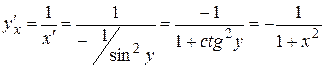
Основные теоремы дифференциального исчисления
Т. Ферма
Пусть ф.  непрерывна на
непрерывна на 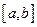 , диф. на
, диф. на  достигает своего наибольшего и наименьшего значения:
достигает своего наибольшего и наименьшего значения:
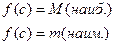

Д.
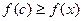
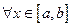
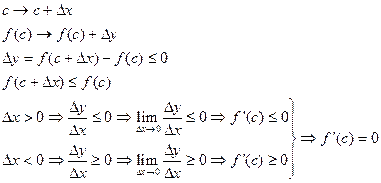
Т. Ролля.
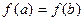
 непрерывна на
непрерывна на 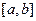 , диф. на
, диф. на 
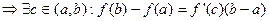
Д.
Наибольшее  , наименьшее
, наименьшее  .
.

1) 
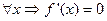
2) 

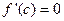

Т. Логранжа.
 непрерывна на
непрерывна на 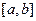 , диф. на
, диф. на 
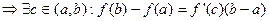
Д.
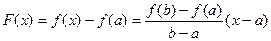
 непрерывна на
непрерывна на 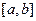 , диф. на
, диф. на 




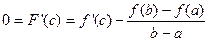
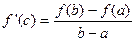 - угловой коэф. конст.
- угловой коэф. конст.
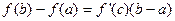
 ,
, 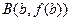
 =k
=k
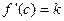
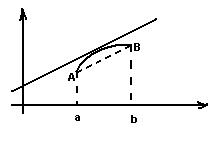
Т. Коши.
 непрерывна на
непрерывна на 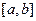 , диф. на
, диф. на 

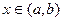
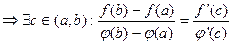
Д.
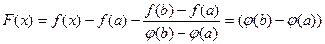
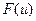 непрерывна на
непрерывна на 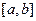 , диф. на
, диф. на 


Теорема Логранжа – частный случай теоремы Коши
Т. Лопиталя 
 удовлетворяют условиям т. Коши
удовлетворяют условиям т. Коши
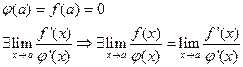
Д.
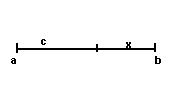


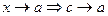
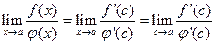
Замечание.
Вместо 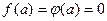 можно
можно 
Применение дифференциального исчисления к исследованию функций.
1.Монотонность
Теорема 1(необходимое условие монотонности)
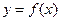 - непрерывна и дифференцируема
- непрерывна и дифференцируема
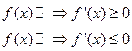
Доказательство

Теорема 2 (достаточное условие монотонности)
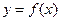 - непрерывна и дифференцируема
- непрерывна и дифференцируема
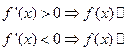
Доказательство
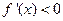

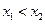 (две произвольные точки)
(две произвольные точки)


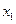 C
C 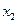
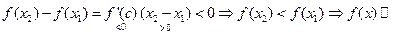
2. Экстремумы
Определение. 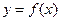 определена в окрестности
определена в окрестности 
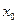 - точка максимума функции, если
- точка максимума функции, если 
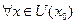
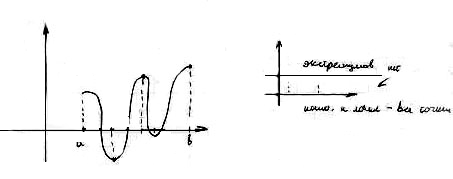
Теорема 1. (Необходимое условие экстремума)
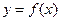 - непрерывна и дифференцируема в
- непрерывна и дифференцируема в 
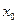 - точка экстремума функции
- точка экстремума функции

Доказательство.

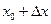
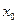
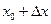
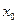 - точка минимума
- точка минимума 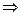
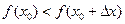


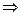
 ;
;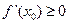

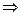
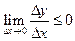 ;
;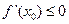
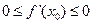
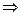
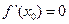 .
.
Стационарные точки – точки, в которых производная равна нулю.
Критические точки – точки, в которых производная равна нулю или имеет разрыв.
|
|
|
Экстремумы могут находится только среди критических точек.
Теорема 2.(достаточное условие экстремума)
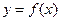 - непрерывна
- непрерывна  и дифференцируема в
и дифференцируема в 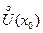
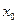 - критическая точка
- критическая точка
 - точка минимума
- точка минимума
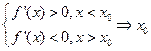 - точка максимума
- точка максимума
Доказательство.
C

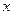
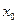
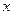
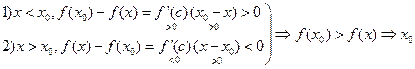 - точка минимума
- точка минимума
Теорема 3.(Исследование на экстремум с помощью второй производной)
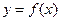 - непрерывна в
- непрерывна в 
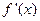 - непрерывна в
- непрерывна в 
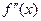

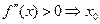 - точка максимума
- точка максимума
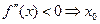 - точка минимума
- точка минимума
Доказательство.

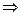
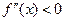 ,
,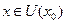

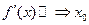 - точка максимума
- точка максимума
3.Вогнутость.
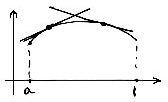
Кривая называется вогнутой вверх (выпуклой), если она лежит ниже касательной проведённой в любой точке отрезка.

Если кривая лежит выше касательной то она вогнута книзу или просто вогнута.
Теорема 1. (необходимое условие вогнутости)
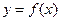 - непрерывна и дифференцируема
- непрерывна и дифференцируема
Если 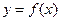 вогнута кверху
вогнута кверху 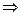
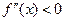
Если 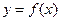 вогнута книзу
вогнута книзу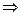
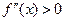
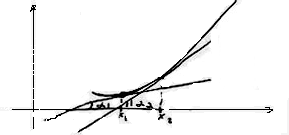 Доказательство. (нестрогое доказательство)
Доказательство. (нестрогое доказательство)
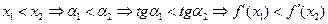
Если кривая вогнута книзу то первая производная возрастает.

Теорема 2. (достаточное условие вогнутости)
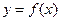 - непрерывна и дифференцируема
- непрерывна и дифференцируема
Если 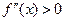 , то
, то 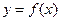 вогнута книзу
вогнута книзу
Если 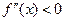 , то
, то 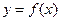 вогнута кверху
вогнута кверху
Доказательство.
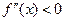
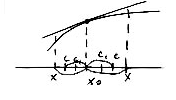
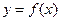 - кривая
- кривая
 - касательная
- касательная

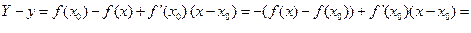

 справа и слева. Ч.Т.Д.
справа и слева. Ч.Т.Д.
4.Перегибы.
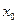 -точка перегиба кривой
-точка перегиба кривой 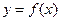 если с одной стороны она вогнута кверху, а с другой вогнута книзу.
если с одной стороны она вогнута кверху, а с другой вогнута книзу.

Теорема 1.(необходимое условие перегиба)
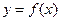 - непрерывна и дифференцируема в
- непрерывна и дифференцируема в 
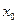 -точка перегиба
-точка перегиба 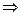
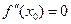
Доказательство.
Точка перегиба - точка экстремума для производной в критических точках второго порядка, нужно искать экстремумы.
Теорема 2.(достаточное условие перегиба)
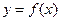 - непрерывна в
- непрерывна в 
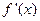 - непрерывна в
- непрерывна в 
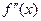 - непрерывна в
- непрерывна в 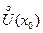
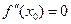 или
или 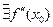
Если производная второго порядка меняет знак при переходе через точку 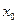 , то
, то 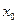 -точка перегиба.
-точка перегиба.
Доказательство.
Следует из основного условия для экстремума.
5.Асимптоты.
1) Вертикальные асимптоты
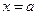 называется асимптотой
называется асимптотой 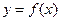 , если
, если 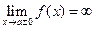
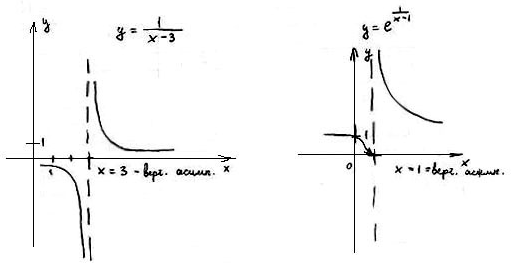
2) Наклонные асимптоты
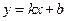 называется наклонной асимптотой
называется наклонной асимптотой 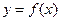 , если
, если 
 называется асимптотической кривой для
называется асимптотической кривой для 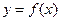 , если
, если 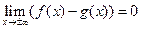
Вывод уравнения наклонной асимптоты.
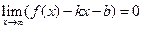 (1)
(1)

 подставляем в формулу (1)
подставляем в формулу (1)
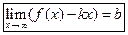
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 362; Нарушение авторских прав?; Мы поможем в написании вашей работы!