Спектральная плотность

Лекция 5.

Введем понятие спектральной плотности (интенсивности) стационарного случайного процесса , определив ее как преобразование Фурье от корреляционной функции:

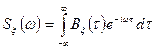. (3.12)

На основании обратного преобразования Фурье можем написать

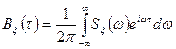. (3.13)

Формулы (3.12) и (3.13) называются соотношениями Винера – Хинчина.

Используя свойство четности (3.8) корреляционной функции, формулы Винера – Хинчина (3.12) и (3.13) можно записать иначе:

.

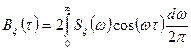. (3.14)

В отличие от спектрального анализа детерминированных сигналов спектральная плотность случайного процесса не дает возможности восстановить какую-либо реализацию процесса, так как она не содержит сведений о фазах отдельных спектральных составляющих. Можно найти множество различных случайных функций (например, путем трансформации фазового спектра), имеющих одинаковую спектральную плотность и функцию корреляции [2].

Для процесса подстановка 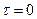в соотношение (3.13) дает

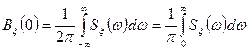. (3.15)

Если среднее значение случайного процесса равно нулю, то из выражения (3.15) с учетом (3.7) получим

. (3.16)

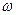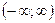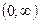Выражение (3.16) можно трактовать как спектральное разложение средней мощности по частотам в пределах или [4].

Если понимать под флуктуационный ток (напряжение), то величину 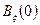можно рассматривать как среднюю мощность, выделяемую этим током (напряжением) на сопротивлении нагрузки 1 Ом. Поэтому функция 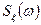характеризует распределение мощности по спектру. Функцию 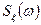иногда называют спектром мощности или энергетическим спектром, так как она имеет размерность энергии.

Корреляционная функция 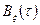и спектральная плотность 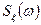стационарного случайного процесса обладают всеми свойствами, характерными для пары преобразований Фурье. В частности, чем «шире» спектр 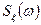, тем «уже» корреляционная функция 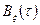, и наоборот.

Введем энергетическую ширину спектра , определив ее формулой

,

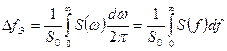где 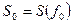значение спектральной плотности при частоте 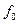, равной максимуму спектральной плотности.

На рис. 3.4 показано соотношение энергетической ширины спектра и ширины спектральной плотности 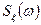на уровне .

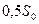Заметим, что интервал корреляции связан с энергетической шириной спектра . Оказывается [1], что произведение интервала корреляции на энергетическую ширину спектра есть приближенно постоянная величина.

3.5.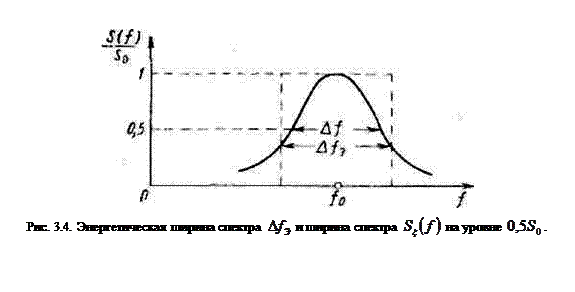
Взаимная спектральная плотность

Пусть имеется два стационарных и стационарно связанных случайных процесса и 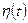с функциями взаимной корреляци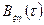и и 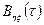. По аналогии со спектральной плотностью (3.12) можно рассматривать взаимные спектральные плотности

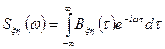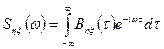, . (3.17)

На основании обратного преобразования Фурье можем написать

, .

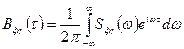Поскольку функции взаимной корреляции не обязательно являются четными, то взаимные спектральные плотности не обязательно будут действительными функциями. Однако если случайные процессы и 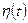действительные, а не комплексные, то взаимные корреляционные функции будут также действительными.

Воспользовавшись формулой (3.8), можно показать, что

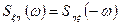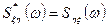, . (3.18)

Дата добавления: 2014-01-06