
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод интегральных преобразований
|
|
|
|

Метод интегральных преобразований является одним из наиболее распространенных методов решения дифференциальных уравнений как обычных, так в частных производных. Ранее (см. §4, гл.2) мы рассмотрели метод преобразования Лапласа решения ОДУ и уравнений в частных производных. Однако, кроме преобразования Лапласа и Фурье (см. §5, гл.3) существуют и другие интегральные преобразования, например, Ханкеля, Меллина, Вебера и др.
Мы воспользуемся синус-преобразованием Фурье

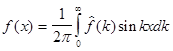 (1)
(1)
для решения следующей задачи.
Задача. Полубесконечное тело, ограниченное плоскостью  имеет заданное начальное распределение температуры
имеет заданное начальное распределение температуры 
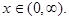 Найти последующее распределение температуры в теле, считая, что с момента времени
Найти последующее распределение температуры в теле, считая, что с момента времени 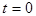 его граница поддерживается при нулевой температуре.
его граница поддерживается при нулевой температуре.
Решение. Математическая модель этой задачи следующая: найти решение уравнения теплопроводности
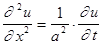 (2)
(2)
с начальным условием 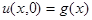 (3)
(3)
и граничным условием 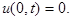 (4)
(4)
Будем считать, что 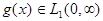 и имеет односторонние производные. Неизвестная функция
и имеет односторонние производные. Неизвестная функция  вместе со своими производными до второго порядка. Тогда, используя преобразование (1), вместо (2-4) получим
вместе со своими производными до второго порядка. Тогда, используя преобразование (1), вместо (2-4) получим 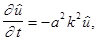 (2')
(2')
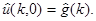 (3')
(3')
Решение ОДУ с постоянными коэффициентами с начальным условием (3') имеет вид
 (5)
(5)
Используя обратное синус-преобразование Фурье (1), найдем
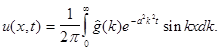 (6)
(6)
Легко проверить, что (6) удовлетворяет граничному условию (4) и является решением данной задачи. В частности, если  то
то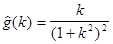 и
и
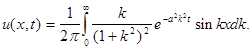 (7)
(7)
§6. Метод разделения переменных
Метод разделения переменных (метод Фурье) - самый распространенный метод решения краевых задач в ограниченной области. Суть метода состоит в представлении решения в виде ряда Фурье по некоторой ортогональной системе функций. Продемонстрируем этот метод на следующей задаче.
|
|
|
Задача. Найти поперечные колебания круглой мембраны радиуса 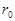 с закрепленным краем, вызванные сосредоточенным ударом, передавшим мембране в ее центре импульс k.
с закрепленным краем, вызванные сосредоточенным ударом, передавшим мембране в ее центре импульс k.
Решение. Задача сводится к решению волнового уравнения  (1)
(1)
с граничным условием
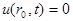 (2)
(2)
и начальными условиями
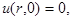
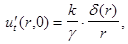 (3)
(3)
где 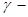 плотность мембраны,
плотность мембраны, 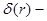 дельта-функция.
дельта-функция.
Запишем оператор Лапласа в цилиндрической системе координат (§9 гл.9, ч.1), учитывая, что отклонение u не зависит от z и угла 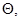

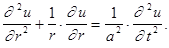 (1')
(1')
Решение будем искать в классе функций, представимых в виде произведения
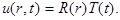 (4)
(4)
Подставляя (4) в (1'), получим 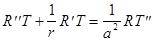

 (5)
(5)
Т.к. правая часть (5) зависит только от t, а левая только от r, то эти части являются постоянной величиной. Обозначим ее 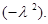 Тогда получим два обыкновенных дифференциальных уравнения (разделим переменные)
Тогда получим два обыкновенных дифференциальных уравнения (разделим переменные)
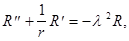 (6)
(6)
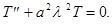 (7)
(7)
Обозначив оператор 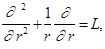 перепишем (6) так:
перепишем (6) так: 
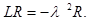 (6')
(6')
Из (6') видно, что 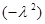 является собственным числом оператора L, а R - собственной функцией, отвечающей собственному числу
является собственным числом оператора L, а R - собственной функцией, отвечающей собственному числу 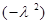 (см. §5 гл.7, ч.1).
(см. §5 гл.7, ч.1).
Собственные функции 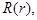 очевидно, удовлетворяют граничному условию
очевидно, удовлетворяют граничному условию 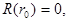 (2')
(2')
а собственные функции  начальному условию
начальному условию  (3')
(3')
Уравнение (6) есть уравнение Бесселя (см. §17 гл.8, ч.1), его решением является 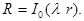 Требуя выполнения граничного условия (2'), найдем собственные числа.
Требуя выполнения граничного условия (2'), найдем собственные числа. 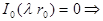
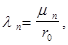
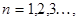
 корни функции Бесселя
корни функции Бесселя 
Подставляя найденные собственные числа 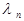 в (7), найдем решение этого уравнения с учетом начального условия (3'). Решение (7) запишем в виде
в (7), найдем решение этого уравнения с учетом начального условия (3'). Решение (7) запишем в виде
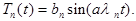 (8)
(8)
Предполагая, что искомая функция  разложим ее в ряд Фурье по ортогональной с весом
разложим ее в ряд Фурье по ортогональной с весом  системе функций Бесселя
системе функций Бесселя
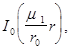
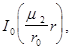

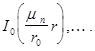 (9)
(9)
С учетом представлений (4) и (8) ряд Фурье запишем в виде
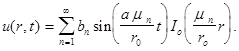 (10)
(10)
Потребуем теперь выполнения второго начального условия (3). Дифференцируя (10) по t при 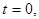 получим следующий ряд Фурье
получим следующий ряд Фурье
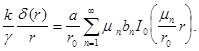 (11)
(11)
Коэффициенты 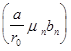 ряда Фурье (11) находятся, как известно (см. (12) §2 гл.3), по формуле
ряда Фурье (11) находятся, как известно (см. (12) §2 гл.3), по формуле 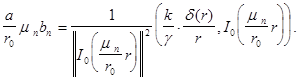 (12)
(12)
Учитывая, что 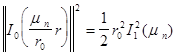 (см. (8) §1 гл.3),
(см. (8) §1 гл.3),
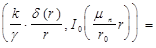
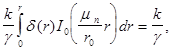 найдем
найдем 
Подставляя эти коэффициенты в (10), получим решение задачи
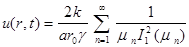
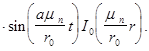
|
|
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 665; Нарушение авторских прав?; Мы поможем в написании вашей работы!