Понятие пространства состояний задачи. Примеры

Goal

Clauses

Predicates

Domains

Пример 5.1.1.

.........

path(A, Z, Graph, Path):-pathl(A, [Z], Graph, Path).

pathl(A, [A | Pathl],._, [A | Pathl]).

pathl(A, [Y I Pathl], Graph, Path):-adjacent! X, Y, Graph),

not member! X, Pathl), % Условие, исключающее образование цикла

pathl! A, [X, Y | Pathl], Graph, Path).

Приведем также программу для поиска пути в корневом графе с корневой вершиной A и множеством дуг ({A} ´ B) È(B ´ C) с

начальной вершиной A и конечной вершиной Z (Z Î C)

/* Программа поиска пути pach(A,Z,A,B,C,P), A- корневая вершина, A´BÈC´D- множество дуг, Z- целевая вершина, P – путь из A в Z * /

s=symbol

l=s*

mr(s,l)

du(s,s,s,l,l)

pach(s,s,s,l,l,l)

mr(X,[X|T]).

mr(X,[Y|T]):-mr(X,T).

du(X,Y,A,B,C):-X=A,mr(Y,B);mr(X,B),mr(Y,C).

pach(X,X,A,B,C,[X]).

pach(X,Z,A,B,C,P):-du(X,Y,A,B,C),pach(Y,Z,A,B,C,P1),P=[X|P1].

pach(A,Z,A,B,C,P),write(P),nl,fail.

Выбрав, например, A = a, B= [b1,b2], C= [c1, c2, c3, c4], Z= c3, и выполнив программу, получим два решения: [a, b1, c3], [a, b2, c3].

Эту программу и приведенный ранее фрагмент программы, можно модифицировать для поиска пути в размеченном графе, например, в графе путям которого поставлены в соответствие стоимости. Стоимость пути пред­ставляет собой сумму стоимостей дуг в этом пути; длину пути можно рассматривать как стоимость, назначая отдельной дуге стоимость, равную 1.

Пространством состояний задачи называется граф такой, что решение задачи сводится к поиску в нем пути с определенными свойствами. В пространстве состояний задачи вершины графа соответствуют ситуациям, а дуги — переходам от одних ситуаций к другим -- этапам решения задачи. Одному или нескольким начальным со­стояниям, соответствующим исходной информации поставленной задачи, сопоставляется система ко­рневых вершин графа. Граф также включает одну или несколько целевых вершин, соот­ветствующих завершающей ситуации решения исходной задачи. Поиск в пространстве состояний характеризует решение задачи как процесс нахождения пути от начального состояния к целевому.

Пример 5.2.1. Задача коммивояжера

Коммивояжер должен посетить четыре города и возвратиться до­мой. Задача состоит в том, чтобы найти кратчайший путь. На рис. 5.4a). дан пример этой задачи. Вершины графа представляют города, а метка на каждой дуге указыва­ет стоимость путешествия по ней. Эта стоимость может означать длину отрезка пути в километрах, если коммивояжер пользуется автомобилем, или цену авиабилета при ис­пользовании самолета. Для удобства предположим, что коммивояжер проживает в городе А и должен вернуться в город А.

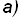
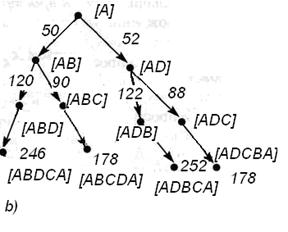
Рис. 5.4.a). Схема,представляющая задачу коммивояжера с четырьмя городами.

b).Граф- пространство состояний задачи п.a).

Будем представлять ситуации, отражающие продвижение коммивояжера, последовательностями букв, обозначающих города. Тогда пространством состояний задачи будет граф, изображенный на рис. 5.4.b). Разметка графа отражает длины путей от вершин до исходной вершины A. Минимальную длину имеют два пути

[ABCDA], [ADCBA],

которые соответствуют одному маршруту, проходимому в противоположных направлениях. В общем случае исчерпывающий поиск в задаче коммивояжера состоит в переборе (N- 1)! вариантов, где N — число городов. При больших N прямой перебор всех путей для поиска минимального будет практически неосуществим. Так уже при N= 36 пространство состояний задачи коммивояжера будет иметь около 10⁴⁰ вершин.

Пример 5.2.2. Игра. 8-головоломка

В этой головоломке 8 занумерованных фишек можно передвигать в пространстве из 9 клеток на квадратной доске.

Цель иг­ры — найти такую последовательность перемещений фишек в пустую клетку, которая привела бы к заранее заданной целевой конфигурации.

Это традиционный пример в литературе по искусственному интеллекту, так как с одной стороны, пространство состояний этой игры является достаточно большим, чтобы представлять интерес, а с другой — вполне дос­тупным для анализа (число возможных состояний составляет 9!, если различать сим­метричные состояния). Состояния игры легко представимы. Игра достаточно богата для апробации интересных эвристик.

Ходы в головоломке заключаются в перемещении фишек ("передвинуть фишку 7 вправо при условии, что пустая клетка расположена справа от нее" или "переместить фишку 3 вниз"), однако значительно удобнее говорить о "перемещении пустой клетки". Это упрощает определение хода, так как в игре участвуют 8 фишек и только одна пустая клетка. Допустимыми являются следующие ходы.

■

Переместить пустую клетку вверх ­.

Переместить пустую клетку вправо —> Переместить пустую клетку вниз ¯.

Переместить пустую клетку влево <—.

Чтобы сделать очередной ход, необходимо удостовериться, что пустая клетка не вый­дет за пределы игрового поля. Поэтому в определенных ситуациях некоторые из четырех ходов могут оказаться недопустимыми. Например, если пустая клетка находится в одном из углов, то допустимы лишь два хода. Если определены начальное и конечное состоя­ние в 8-головоломке, то процесс решения задачи можно описать явно (рис.5.5). Состоя­ния описываются массивом размерности 3x3. Предикатное представление требует ис­пользования предиката состояния с девятью параметрами (для локализации фишек на доске). Дуги в пространстве состояний определяют четыре процедуры, описывающие возможные перемещения пустой клетки.

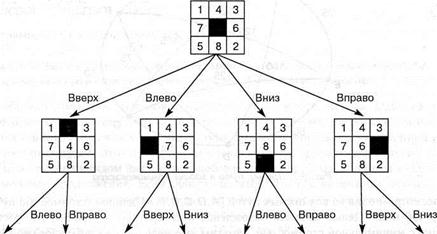
Рис.5.5. Пространство состояний 8-головоломки, порожденное "перемещением пустой клетки"

Пространство состояний этой игры является графом, большинство вершин которого имеет много предков; в этом графе возможны циклы. Множество целевых состояний, или

— это заранее определенное множество конфигураций. Если одна из них встречается на пути, поиск прекращается. Путь из начальной вершины в целевую — искомая последова­тельность ходов.

Отметим, что полное пространство состояний 8-головоломки состоит из двух несвязных подграфов (одинакового размера). Отсюда сле­дует, что ровно половина состояний являются недостижимыми из любой заданной на­чальной вершины. Если поменять местами (вопреки правилам!) две соседние фишки, все состояния из другой части пространства состояний окажутся достижимыми.

Пример 5.2.3. Задача перестановки кубиков(см.1).

Задача состоит в том, что необхо­димо найти план переупорядочения кубиков, поставленных друг на друга, как пока­зано на этом рисунке 5.6. Разрешается передвигать одновременно только один кубик. Кубик можно передвигать, только если на нем не стоит другой кубик. Такой кубик можно поставить на стол или на другой кубик (кубики, поставленные друг на друга, образуют столбик). Чтобы определить требуемый план, нужно найти последователь­ность действий, позволяющих осуществить указанную перестановку кубиков.

В первоначальной ситуации имеется только один вариант: поставить ку­бик С на стол. А после того как кубик С поставлен на стол, появляются три следую­щих варианта:

■ поставить А на стол;

■ поставить А на С;

■ поставить С на А.

Рис.5.6. Задача перестановки кубиков

Пространство состояний для этой задачи показано на рис.5.7. Узлы этого графа соответст­вуют ситуациям, а дуги — допустимым переходам от одной ситуации к другой. Задача поиска плана решения эквивалентна поиску пути между заданной начальной ситуацией (начальным узлом) и некоторой указанной конечной ситуацией- целевым узлом.

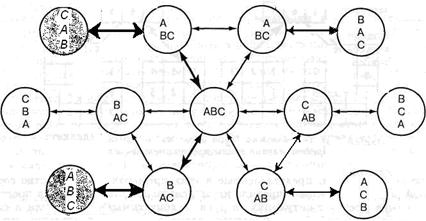
Рис. 5.7. Пространство состояний задачи перестановки кубиков; полужирными стрелками обозначен путь решения задачи, пред­ставленной на рис. 5.6.(Братко,1).

Пример 5.2.4. Задача об обезьяне и бананах.

Для описания некоторых бесконечных пространств состояний возможно использование переменных так, что выражения, содержащие переменные, могут быть исполь­зованы для описания некоторого конечного разбиения множества состояний. Подстановка каких-то частных значений (констант) вместо этих переменных в указанные выражения дает конкрет­ные описания состояний. Такого рода выражения называются схемами описания состояний.

Иллюстрацией к сказанному может служить описание пространства состояний следующей широко известной задачи.

В комнате, где находится обезьяна, имеются ящик и связка бананов, причем бананы подвешены к потолку настолько высоко, что обезьяна не может дотянуться до них с пола. Какая последовательность действий позволит обезьяне достать эти бананы? (Предполагается, что обезьяна должна подойти к. ящику, подтащить его к бананам, забраться на него и.достать бананы.)„

Как следует строить для этой задачи представление в про­странстве состояний? В описании состояния должны входить следующие элементы: координаты обезьяны в ком­нате (по горизонтали и по вертикали), координаты ящика в ком­нате и наличие у обезьяны бананов. Эти элементы удобно пред­ставить в виде четырехэлементного списка (w, x, у, г), где

w — координаты обезьяны в горизонтальной плоскости (двумерный вектор),

х — это 1 или 0 в зависимости от того, где обезьяна нахо­дится, на ящике или нет,

у — координаты ящика в горизонтальной плоскости (дву­мерный вектор),

z — это 1 или 0 в зависимости от того, достала обезьяна бананы или нет.

Множество конкретных значений списка (w, x, у, г) бесконечно,поэтому интерпретируя отдельные списки как состояния,получим бесконечное пространство состояния. Вместе с тем, принимая за состояние схемы с переменными векторами w, y, придем к конечному пространству (пространству схем), представляющему данную задачу.

Операторы в этой задаче, задающие переходы от одной схемы к другой соответствуют четырем возмож­ным действиям, которые могут выполняться обезьяной:

1) подойти (u) - обезьян а идет к точке u в плоскости пола комнаты,

2) передвинуть (v) - обезьяна передвигает ящик в точку v пола комнаты,

3) взобраться - обезьяна забирается на ящик,

4) схватить - обезьяна хватает бананы.

Соответствующие преобразования схем таковы:

(w, 0, у, z) -> (u, 0, у, z),

(w, 0, w, z) > (v, 0, v, z),

.

(w, 0, w, z)----------- > (w, 1, w, z),

(с, 1, с, 0)- > (с,1, с, 1),

где с — координаты точки пола, расположенной непосред­ственно под бананами (двумерный вектор).

Применение некоторых операторов, например «передвинуть», связано с ограничением значений переменных, представляющих координаты обезьяны и ящика, от которых теперь требуется, чтобы они были одинаковыми. Две схемы считаются идентичными, если они отличаются лишь наименованием переменных.

В такой формулировке элементы множества целевых со­стояний описываются любыми списками, последний элемент которых есть единица.

Предположим, что вначале обезьяна находится в точке а пола, а ящик – в точке b. Тогда начальное состояние будет задаваться списком (а, 0, b, 0). Единственный оператор, который применим в этом состоянии, это «подойти», приводящий к схеме (u, 0, b, 0). Теперь применимы три оператора. Если u = b, то обезьяна мо­жет либо забраться на ящик, либо передвинуть его. Независимо от величины u обезьяна могла бы переместиться куда-нибудь еще. Влезание на ящик приводит к состоянию с описанием (b, 1, b, 0); перемещение ящика в v приводит к схеме (v, 0, v, 0), а переход в другое место, описываемое новой переменной, не из­меняет описания.

Продолжая процесс применения всех операторов, по­строим пространство состояний, иллюстрируемое графом на рис.5.8. Полученный граф невелик и на нем легко можно найти путь, решающий нашу задачу (жирные

Начальная вершина

подойти (u)

положить u = b ,передвинуть(v)

передвинуть(v)

положить u= v

положить v = с

Целевая вершина

Рис 5.8. Граф для задачи об обезьяне и бананах (Нильсон,3).

стрелки). Подставив вместо переменных их соответствующие частные значения, как это показано на рис.5.8, получаем последовательность операторов: подойти (b), передвинуть (с), взобраться, схватить.

Дата добавления: 2014-01-07