Метод множителей

Метод назван так потому, что в нем наряду со штрафной функцией используются множители Лагранжа.

Предположим вначале, что ограничения заданы только сис­темой равенств h(x)=0. Таким образом, как и раньше, обозначим компоненты вектора h(x) h_i(x) = 0, i = 1, m.

Запишем модифицированную функцию Лагранжа, добавив в нее штрафную функцию в виде квадратичного штрафа:

L_k(x, λ) = f(x) – λ(k)^T h(x) + 1/2C(k) ||h(x)||²,

где ||h(x)||² = 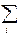h_i²(x);

λ(k) - вектор множителей;

C(k) - возрастающая числовая последовательность;

k - индекс итерации.

Таким образом, как и в методе штрафных функций на k-й итерации решается задача поиска безусловного минимума:

min L_k(x, λ(k)), где минимум берется по х;

C(k) вычисляется по одной из двух формул: C(k) = kC(k - 1) или C(k) = kβ, где β = 4... 10, а расчет множителей производится в соответствии с выражением 2:

λ(k) = λ(k - 1) - C(k - 1)h(x^*(k - 1)) (2)

Здесь, как и раньше, x^*(k - 1) обозначает точку безусловного минимума функции L_k-1(x, λ) на (k-1)-й итерации. Точка эта, в свою очередь, является начальной точкой поиска на k-й итерации.

Поскольку последовательность C(k) возрастает относительно медленно, а функции h_i(x^*(k)) стремятся к нулю (в противном случае большой штраф не дает минимума функции L_k(x, λ)), то последова­тельности λ_i(k) сходятся к некоторым числам.

Решение задачи, как и в методе штрафных функций, фикси­руется по условию:

||x^*(k) – x^*(k-1)||<ε_x

Пусть теперь среди ограничений имеются также и неравенства g_j(x)>=0. Превратим их в эквивалентные равенства:

_i(x, z) = g_j(x) – z_j² =0.

Тогда модифицированная функция Лагранжа будет иметь вид

L_k(x,z,λ,μ) = f(x) – λ^T(k)h(x) + 1/2C(k)||h(x)||² – μ^T(k)(x) + 1/2C(k)||_* *(x)||²,

где μ(k) - вектор множителей μ_j(k) (j = 1, r) при фиктивных равенствах _j(x).

Аналогично формуле (2) для расчета μ_j(k) запишем:

μ_j(k) = μ_j(k - 1) - C(k - 1)(x^*(k - 1)). (3)

Итак, в результате требуется решить последовательность за­дач минимизации модифицированной функции Лагранжа:

min L_k(x,z,λ,μ) по x и z для k = 1, 2, ….

Но минимум по z, если считать x параметром, можно найти аналитически в явном виде, записав соответствующие частные про­изводные и приравняв их к нулю.

В результате указанных операций получим вектор z^* на k-й итерации, компоненты которого рассчитываются по формуле:

(z_j^*(x))² = max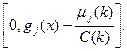

Подставив это выражение в формулу (3) для расчета μ_j(k),

где (x^*(k - 1)) = g(x^*(k - 1)) - (z_j^*(k - 1))²,

получим: μ_j(k) = max (0, μ_j(k -1) - C(k -1) g_j(x^*(k - 1))).

То же самое значение z_j^*(k) нужно подставить в формулу для модифицированной функции Лагранжа.

Отметим, что факт записи некоторой вспомогательной функ­ции, которую мы назвали целевой, является общим приемом для по­следних трех методов.

Дата добавления: 2014-01-07