Передаточные функции

Или

Общая форма записи системы дифференциальных уравнений может быть представлена в виде

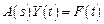
a ₁₁(s) y ₁ + a ₁₂(s) y ₂ +... + a _{1 k} (s) y_k = f ₁(t)

a ₂₁(s) y ₁ + a ₂₂(s) y ₂ +... + a _{2 k} (s) y_k = f ₂(t)

………………………………. (2.10)

a_{k 1}(s) y ₁ + a_{k 2}(s) y ₂ +... + a_kk (s) y_k = f_k (t),

где

− a_ij (s) – коэффициенты, возможно зависящие от некоторого параметра s;

− y ₁, y ₂,..., y_k − обобщенные координаты системы, в том числе ошибка d (t) и регулируемая величина y (t);

− f ₁(t), f ₂(t),..., f_k (t) − внешние координаты, определяющие задающие g (t) и возмущающие f (t) воздействия.

Для удобства и формализации решений систему уравнений (2.10) можно также разрешить относительно:

− регулируемой величины − y (t);

− ошибки − d (t).

Преобразование Лапласа. Кроме непосредственно дифференциальных уравнений, в теории автоматического управления используются различные их преобразования, так как решение дифференциальных уравнений высокого порядка вызывает значительные трудности. Поэтому решения дифференциальных уравнений исследуются косвенными методами. Наиболее удобным из таких методов является алгебраизация дифференциальных уравнений применением преобразования Лапласа.

Преобразованием Лапласа называют преобразование функции f (t) переменной t в функцию F (p) другой переменной 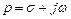(оператор Лапласа − комплексное число) с помощью интеграла

.

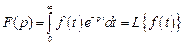Функция f (t) называется оригиналом функции комплексной переменной F (p), F (p) – изображением функции f (t).

Из теории функций комплексной переменной известна формула обращения, позволяющая получить функцию-оригинал f (t) по ее изображению F (p):

,

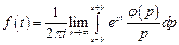где s выбирается так, чтобы все особые точки (корни подынтегральной функции) лежали правее прямой Re p = s. Будем обозначать прямое преобразование Лапласа функции символом 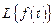, а обратное – символом .

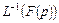Свойства преобразования Лапласа определяются следующими теоремами:

1. Теорема суперпозиции. Изображение суммы равно сумме изображений слагаемых:

L { f (t) + g (t)} = L { f (t)} + L { g (t)} = F (p) + G (p).

2. Изображение постоянной величины есть постоянная, делен-

ная на оператор p:

.

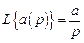3. Теорема линейности. Умножение оригинала на постоянную величину A влечет умножение изображения на эту постоянную:

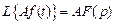
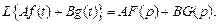
4. Теорема запаздывания. Для любого постоянного t> 0 и функциисправедливо

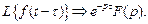
5. Теорема дифференцирования оригинала. Если

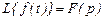, то

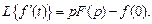
Применив эту теорему к производным высших порядков, получим

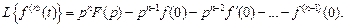(2.11)

При нулевых начальных условиях выражение (2.11) упрощается

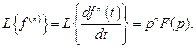
Другими словами, изображение производной n -го порядка соответствует умножению оператора p степени n на изображение функции при нулевых начальных условиях.

6. Теорема интегрирования оригинала. Если 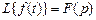, то

.

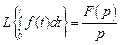Изображение интеграла кратности n функции f (t) соответствует умножению изображения функции на 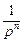при нулевых начальных условиях:

.

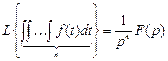7. Теорема о начальном значении оригинала:

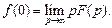
8. Теорема о конечном значении оригинала:

.

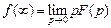9. Теорема подобия (изменение масштаба). Если аргумент функции умножен на постоянное число a, то это соответствует умножению на 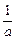изображения и аргумента изображения

.

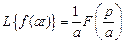Преимущества преобразования Лапласа проявляются, прежде всего, в представлении дифференциальных уравнений алгебраическими, а также в возможности описания закона функционирования систем в форме передаточных функций.

Понятие передаточной функции. Понятие передаточной функции системы является основополагающим в классической теории автоматического управления. В общем случае передаточная функция 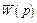есть соотношение между входными и выходными переменными объекта или системы в операторной форме при нулевых начальных условиях. Зная передаточную функцию и изображение переменной входа, легко найти изображение выхода

,

т.е. передаточная функция по существу есть операторный коэффициент передачи системы.

Понятие передаточной функции было введено при изучении скалярных систем, а затем расширено на многосвязные. Удобство этого понятия состоит в том, что оно:

– позволяет в алгебраической форме отобразить соотношение между входом и выходом.

– допускает простую структурную интерпретацию;

– позволяет выявить ряд типовых элементов систем автоматического управления;

– тесно связано с понятием частотной характеристики (см. далее).

Передаточная функция скалярных систем. Пусть имеем дифференциальное уравнение (2.1), описывающее поведение скалярной системы.

Используя свойства преобразования Лапласа, перепишем (2.1) в изображениях при нулевых начальных условиях:

.

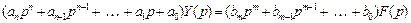Тогда по определению, передаточная функция есть

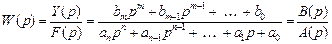, (2.12, а)

где A (p), B (p) – операторные представления соответственно полиномов знаменателя и числителя передаточной функции.

Выражение (2.12, а) – это так называемая, полиномиальная форма передаточной функции. Корни полинома числителя передаточной функции называются нулями системы, корни характеристического уравнения – полюсами системы. В реальных системах m ≤ n (иначе наступает неуправляемый внешними сигналами режим генерации).

В теории автоматического управления W (p) принято записывать в нормированном виде, когда свободные члены в полиномах A (p) и B (p) равны 1:

,

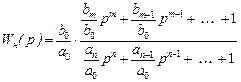где 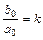– статический коэффициент передачи (усиления) элемента или системы.

Помимо этого оператор связи входа и выхода можно задать коэффициентом и множествами нулей (корней полинома числителя) z_j, j = 1,…, m и полюсов (корней полинома знаменателя) s_i, i = 1,…, n:

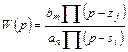. (2.12, б)

В результате получим так называемую факторизованную форму передаточной функции.

Пример 2.3. Пусть система описывается дифференциальным уравнением второго порядка

.

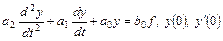Получим операторное представление передаточной функции в полиномиальной и факторизованной формах. Для этого преобразуем уравнение по Лапласу, воспользовавшись свойством линейности оператора преобразования L и теоремой о дифференцировании оригинала

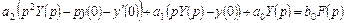
или

.

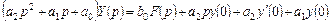Передаточная функция в полиномиальной форме есть отношение изображения выхода к изображению входа при нулевых начальных условиях

.

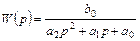Для получения факторизованного представления передаточной функции необходимо решить квадратное уравнение, представляющее полином знаменателя:

.

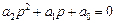Его корни имеют вид

, .

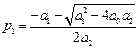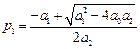Тогда факторизованная форма передаточной функции имеет вид

.

■

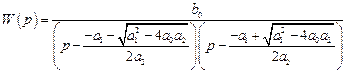Имея передаточную функцию, можно изображать связь между входом U (p) и выходом Y (p) на операторных представлениях структурных схем звеньев или систем в виде, показанном на рис. 2.10.

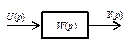
Рис. 2.10. Изображение звена с использованием

передаточной функции

Дата добавления: 2014-01-15