Устойчивость систем управления

Основные требования к системам управления

Основные свойства систем управления

Лекция 11

Анализ систем управления состоит в изучении их системных свойств, условий выполнения ими своих функций и достижения заданных целей.

Безусловными требованиями к системам управления являются:

− устойчивость движений;

− инвариантность управляемой (выходной) переменной к возмущениям и ковариантность ее с заданным воздействием;

− робастность (грубость, параметрическая инвариантность), т.е. нечувствительность свойств системы к вариациям характеристик элементов.

Основными задачами анализа являются:

− установление фактов устойчивости, инвариантности и робастности систем;

− построение характеристик систем и определение показателей их качества.

Понятие устойчивости. Важнейшим свойством систем управления является их устойчивость, т.е. вид реакции системы на возмущающие воздействия различного вида, вызывающие отклонения системы от заданного положения или движения.

Понятие устойчивости можно наглядно продемонстрировать на примере конуса, три возможных положения которого показаны на рис. 4.1.

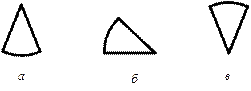
Рис 4.1. Положения конуса: устойчивое (а), нейтральное (б) и неустойчивое (в)

Объект считается устойчивым, если он после кратковременного

внешнего воздействия возвращается в исходное или близкое к нему состояние. При этом объекты могут быть устойчивы в «малом» (при небольших воздействиях) или в «большом» (при больших воздействиях).

В неустойчивом объекте управляемая координата продолжает меняться по окончании сколь угодно малого входного воздействия.

Нейтральный объект по окончании управляющего воздействия переходит в новое состояние равновесия, зависящее от характера воздействия.

Устойчивость динамической системы определяется аналогичным образом: реакция системы на отклонение или начальные условия может затухать (для устойчивой системы), оставаться неизменной по величине (для нейтральной системы) либо нарастать (для неустойчивой системы), как показано на рис. 4.2.

Рис. 4.2. Реакция системы на внешнее воздействие:

устойчивой (а), нейтральной (б) и неустойчивой (в)

Многие реальные системы объективно неустойчивы в разомкнутом состоянии и даже проектируются таковыми. Устойчивость системы обеспечивается с помощью обратной связи, а затем надлежащим выбором параметров регулятора обеспечиваются показатели качества (установившаяся ошибка, величина перерегулирования, время установления выходного сигнала и т.д.). Работоспособной может быть только устойчивая система.

Для устойчивости физически реализуемой системы необходимо и достаточно, чтобы ее весовая функция удовлетворяла условию

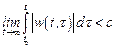, (4.1)

или, что то же самое,

,

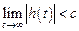где c – некоторая конечная величина, т.е. чтобы выходная реакция системы оставалась ограниченной (величиной c) при ограниченных по абсолютной величине (значением 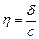, 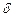− допустимая величина сигнала ошибки) входных возмущениях. Дифференцируя (4.1), получаем условие устойчивости в виде

.

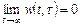Однако это условие необходимо, но недостаточно. В реальных системах входной сигнал часто является комбинацией своих производных. Такие системы в определенном выше смысле всегда неустойчивы (производная входного сигнала может быть в пределе быть бесконечно большой). Поэтому для них устойчивость определяется с учетом отбрасывания из входного сигнала δ-функции и ее производных.

Пример 4.1. Определить условия устойчивости апериодического звена первого порядка, переходная функция которого имеет вид

,

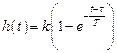а весовая функция есть

.

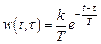Решение. Условие устойчивости этого звена определяется как

.

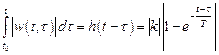Отсюда видно, что при положительной постоянной времени T для любых t ₀ и t интеграл не превосходит абсолютной величины коэффициента усиления апериодического звена k. При неположительном T звено неустойчиво.

■

Устойчивость – собственное свойство системы. Свойство устойчивости линейных систем анализируется по модели типа M_s (система, выделенная из среды) в форме однородных дифференциальных уравнений n -го порядка

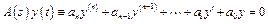(4.2)

или систем уравнений в форме пространства состояний

.

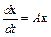Процесс регулирования в этом случае определяется, как известно, решением дифференциального уравнения системы как сумма двух составляющих: частного решения неоднородного уравнения с правой частью (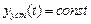– установившееся значение) и общего решения соответствующего однородного уравнения (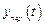– переходная составляющая).

Вынужденные движения неавтономных систем представляются суммой установившихся движений (определяемых полюсами воздействий) и переходных процессов из-за ненулевых начальных условий, вызванных внезапным приложением воздействий. В асимптотически устойчивой системе с течением времени все процессы стремятся к установившимся значениям

,

.

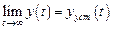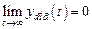Вынужденные движения. Общее решение уравнения (4.2) обычно ищется в форме набора степенных функций вида

.

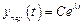Дифференцируя последнее выражение n раз

,

…………..

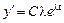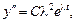
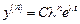
и подставляя результаты в (4.2), после сокращения на общий множитель 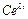получим

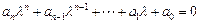. (4.3)

Заменив в (4.3) 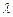на , получим характеристическое уравнение, корни которого 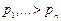будут определять характер переходного процесса в системе, поскольку переходная составляющая описывается в виде

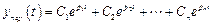, (4.4)

где C_i – постоянные интегрирования, определяемые из начальных условий.

Таким образом, для оценки устойчивости системы управления необходимо, прежде всего, решить характеристическое уравнение и определить его корни. Зависимость устойчивости системы от вида корней определяется для трех случаев (рис. 4.3).

1. Вещественные корни. Если один из корней, например, p_γ, является вещественным, то в зависимости от его значения соответствующее слагаемое в переходной составляющей движения 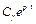будет со временем затухать (при 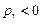), как показано на рис. 4.3, а или возрастать (при ).

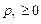2. Комплексные корни. Они бывают попарно сопряженными. При отрицательной вещественной части соответствующие им слагаемые в переходной составляющей движения могут быть представлены в виде

,

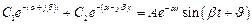где A и 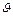– новые постоянные интегрирования.

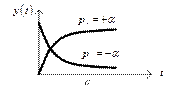
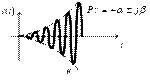
Рис. 4.3. Характер собственных движений системы в зависимости

от вида корней характеристического полинома

В этом случае получаются затухающие синусоидальные колебания (рис. 4.3, б), причем мнимая часть 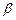есть круговая частота колебаний, а 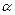– показатель затухания. При положительных вещественных частях корней процесс представляет собой расходящиеся синусоидальные колебания (рис. 4.3, в).

3. Чисто мнимые корни. Для двух сопряженных мнимых кор-

ней составляющая переходного процесса определяется выражением

.

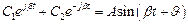Такой процесс представляет собой незатухающие колебания, показанные на рис. 4.3, г.

Свободные движения. Преобразуем дифференциальное уравнение (4.2) по Лапласу с учетом начальных условий:

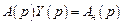. (4.5)

Изображение решения уравнения (4.2) следует из (4.5)

.

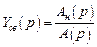Если полином 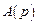имеет только простые корни p_i, i = 1,…, n, то выражение для свободных движений есть

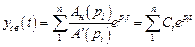, (4.6)

где (′) – символ дифференцирования полинома по p, а

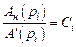
есть вычет.

Если же корни полинома – кратные, то вместо C_i в (4.6) появятся полиномы от t со степенями ниже кратности K корня p_j

.

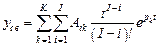Таким образом, для того, чтобы свободная составляющая была затухающей, необходимо чтобы корни были либо вещественными отрицательными или комплексными с отрицательными вещественными частями

,

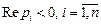т.е. все корни должны находиться левее мнимой оси. Это же условие имеет место и для собственных значений матрицы состояний A.

Таким образом, система устойчива по входу-выходу, если:

− система устойчива по начальным условиям, т.е. ее корни находятся в левой полуплоскости;

− передаточная функция системы физически реализуема, т.е. в ней степень полинома числителя n не превышает степени полинома знаменателя m.

Критерии устойчивости. Выявление устойчивости возможно не только путем определения значений коней полиномов, но и на основе критериев устойчивости, позволяющих с помощью относительно простых вычислений определить, лежат ли все корни в левой полуплоскости. Различают алгебраические (Гурвица и Рауса) и частотные (Найквиста и Михайлова) критерии.

Алгебраические критерии основаны на исследовании зависимостей между видом корней характеристического полинома и значениями коэффициентов полинома при неизвестных. Это позволяет свести задачу исследования системы, описываемой дифференциальным уравнением, к выполнению алгебраических преобразований для нахождения условий, которым должны удовлетворять коэффициенты полинома. Такие условия были найдены в 1877 г. Е. Раусом. Другая форма этих условий была найдена в 1895 г. А. Гурвицем. Суть их заключается в следующем: для того чтобы характеристический полином имел корни только с отрицательными действительными частями, необходимо, чтобы его коэффициенты имели один и тот же знак.

Критерий Рауса. Пусть характеристический полином звена или системы имеет противоположную обычной записи индексацию коэффициентов

.

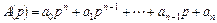Образуем из его коэффициентов матрицу размерности

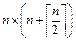
вида

, (4.7)

где 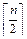– целочисленный остаток от деления n на 2 (значение четности n), элементы двух нижних строк (4.7) есть коэффициенты полинома 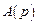, элементы 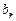следующих двух строк определяются формулами

,

.

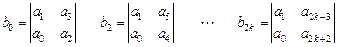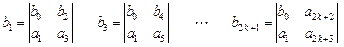Элементы 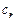следующих двух строк определяются этими же формулами, в которых элементы a и b заменены соответственно элементами b и c.

Раус доказал, что для отрицательности действительных частей корней полинома необходимо и достаточно, чтобы все элементы первого столбца матрицы (4.7) были положительными: .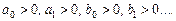

Пример 4.2. Определить условия устойчивости для систем 1 ÷ 4 порядка.

Решение. Для уравнения первого порядка

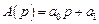
матрица Рауса имеет вид

,

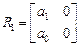величины 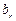и 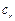равны нулю и условия устойчивости сводятся к 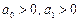. Это условие является необходимым и достаточным.

Для уравнения второго порядка

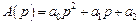
матрица Рауса имеет вид

,

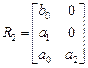где

,

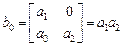а остальные величины 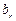и 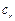равны нулю и условия устойчивости сводятся к 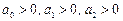. Это условие также является необходимым и достаточным.

Для уравнения третьего порядка

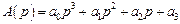(4.6)

матрица Рауса имеет вид

,

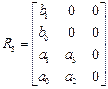где

, ,

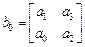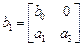т.е. вычисляются элементы 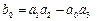и 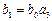, а остальные величины 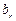и 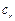равны нулю и условия устойчивости в этом случае принимают вид

,

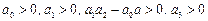т.е. здесь условие положительности коэффициентов полинома необходимо, но не достаточно.

Для уравнения четвертого порядка

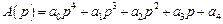
матрица Рауса имеет вид

,

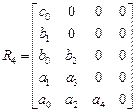где

, , , ,

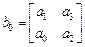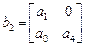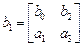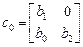т.е. вычисляются элементы 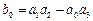, , 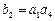, , 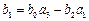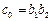а остальные величины 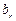и 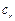равны нулю и условия устойчивости в этом случае принимают вид:

.

■

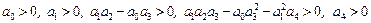Пример 4.3. Для системы, описываемой передаточной функцией с характеристическим полиномом

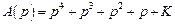, (4.8)

определить, является ли она устойчивой.

Решение. Таблица Рауса для этой системы выглядит так:

,

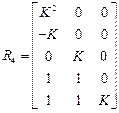так как

, ,

, .

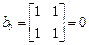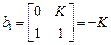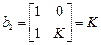Поскольку один из элементов первого столбца матрицы Рауса отрицателен, система неустойчива. Заметим, что система с характеристическим уравнением вида (4.8) неустойчива при любом .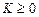

■

Дата добавления: 2014-01-15