
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 12. Критерий Гурвица. Из коэффициентов характеристического
Критерий Гурвица. Из коэффициентов характеристического
полинома 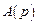 , представленного в виде
, представленного в виде
 , (4.9)
, (4.9)
либо в виде
 ,
,
составляются матрицы Гурвица вида

или
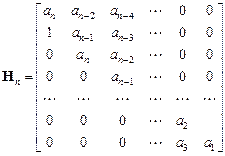 ,
,
представляющие собой квадратные матрицы размера n ´ n. Их диагональными определителями являются:
– в первом случае
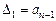 ;
;
 ;
;
 ;
;
…………………..
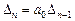 ,
,
а во втором
 ;
;
 ;
;

…………………..
 ,
,
Для асимптотической устойчивости системы необходимо и достаточно, чтобы при  все диагональные определители матриц Гурвица были положительны.
все диагональные определители матриц Гурвица были положительны.
Следствием критерия Гурвица является условие нахождения системы на границе устойчивости. Этим условием является обращение в нуль последнего (старшего) определителя Гурвица, т.е. 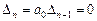 для первой матрицы и
для первой матрицы и  − для второй. Оно распадается на две составляющие:
− для второй. Оно распадается на две составляющие:
− для первой матрицы
 , что соответствует полюсу, равному нулю, и
, что соответствует полюсу, равному нулю, и
 , что соответствует наличию у харак-
, что соответствует наличию у харак-
теристического полинома двух комплексно-сопряженных корней с нулевой вещественной частью;
− для второй матрицы
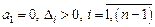 , что соответствует полюсу, равному нулю, и
, что соответствует полюсу, равному нулю, и
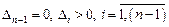 , что соответствует наличию у характеристического полинома двух комплексно-сопряженных корней с нулевой вещественной частью.
, что соответствует наличию у характеристического полинома двух комплексно-сопряженных корней с нулевой вещественной частью.
Пример 4.4. Определить условия устойчивости для системы третьего порядка по критерию Гурвица.
Решение. В первой форме записи полином системы представляется следующим образом
 . (4.10)
. (4.10)
Матрица Гурвица для этого полинома имеет вид

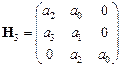 .
.
Если все коэффициенты полинома положительны, то здесь следует проверить только знак определителя
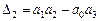 .
.
Для того же полинома во второй форме записи

матрица Гурвица имеет вид
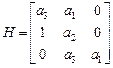 .
.
При положительных коэффициентах полинома для устойчивости системы диагональные определители должны отвечать условиям
 ;
;
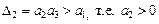 ;
;
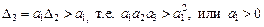 .
.
Таким образом, помимо положительности всех коэффициентов характеристического полинома, условием устойчивости системы является соотношение

■
Как следует из последнего выражения для устойчивости системы третьего порядка необходимо, чтобы произведение средних коэффициентов характеристического полинома было больше произведения крайних (критерий Вышнеградского).
С помощью критерия Гурвица можно строить границы устойчивости и определять области устойчивости системы в пространстве коэффициентов полиномов (параметров системы управления).
Рассмотрим систему третьего порядка с характеристическим полиномом (4.10). Пусть все его коэффициенты положительны. Проведем замену переменных, не приводящую к изменению расположения корней полинома относительно мнимой оси:
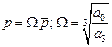 .
.
Тогда получим другой полином

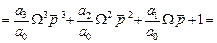

коэффициенты которого равны
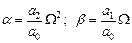
и называются параметрами Вышнеградского. Границе устойчивости в плоскости параметров α и β соответствует гипербола Вышнеградского α β = 1, приведенная на рис. 4.4.
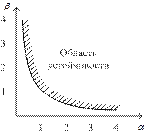
Рис. 4.4. Диаграмма Вышнеградского
Параметр нормировки Ω называется среднегеометрическим корнем, поскольку
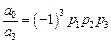 .
.
Для систем высокого порядка определение устойчивости с помощью критерия Гурвица становится трудоемким и избыточным. В этом случае предпочтительнее применение критерия Рауса, позволяющего быстро определить устойчивость системы по коэффициентам характеристического полинома.
Частотные критерии. Частотные характеристики системы
управления содержат много информации для определения ее устойчивости. Эти характеристики могут быть получены экспериментально подачей на вход системы синусоидального воздействия и варьирования его частоты.
Как было показано выше, для определения устойчивости замкнутой системы необходимо исследовать ее характеристическое уравнение
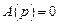 ,
,
или в терминах сигнальных графов
 . (4.11)
. (4.11)
При этом необходимо доказать, что все его корни расположены в левой половине комплексной плоскости. В частотной области эта задача решается отображением графических представлений характеристических полиномов (контуров) на комплексной плоскости.
Отображение контуров на комплексной плоскости. Контур – некоторая замкнутая траектория в плоскости. Поскольку  – комплексная переменная,
– комплексная переменная, 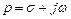 , то любая функция от комплексной переменной
, то любая функция от комплексной переменной  − также комплексная, следовательно, ее можно представить в виде
− также комплексная, следовательно, ее можно представить в виде
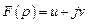
и изобразить на комплексной плоскости в координатах  и
и 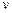 .
.
Пример 4.5. Пусть на плоскости p имеем единичный квадрат, показанный на рис 4.5. Отобразим его на  -плоскость в координатах
-плоскость в координатах  и
и 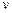 с помощью функции
с помощью функции
 .
.
Решение. Отметим, что отображающая функция имеет один нуль

Рис. 4.5. Комплексный единичный квадрат
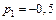 . Выразим координаты в плоскости
. Выразим координаты в плоскости  -
-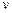 в координатах в
в координатах в
плоскости  :
:
 ,
,
откуда следует
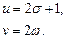
Граничные точки отображения единичного квадрата на  -плоскость приведены в табл. 4.1.
-плоскость приведены в табл. 4.1.
Таблица 4.1
Некоторые координаты отображения единичного
квадрата с помощью функции 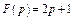
| A | B | C | D | |

| 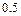
| 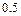
| 
| 
|

| 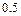
| 
| 
| 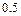
|

| ||||

| –1 | –1 |
Построение отображения единичного квадрата на комплексной плоскости в координатах  и
и 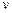 (на
(на  -плоскости) показано на рис. 4.6.
-плоскости) показано на рис. 4.6.

Рис. 4.6. Отображение единичного квадратного контура с помощью функции 
Оно (отображение) представляет собой также квадрат, но со стороной, вдвое большей стороны исходного квадрата, и сдвинутый вправо на единицу. Полученное отображение является конформным, т.е. оно повторяет исходный контур по форме, но в некотором другом масштабе по осям и с некоторым сдвигом. При этом замкнутый контур отображается замкнутым контуром, а направление обхода исходного контура сохраняется в отображении.
Построенный контур:
− не охватывает полюс  , показанный на рис. 4.5 кружком;
, показанный на рис. 4.5 кружком;
− при движении по часовой стрелке охватывает начало координат один раз.
Если отображающая дробно-рациональная функция – другая, например,
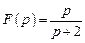
с нулем 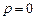 и полюсом
и полюсом  , то отображение единичного квадрата на
, то отображение единичного квадрата на  -плоскости будет также другим:
-плоскости будет также другим:
 .
.
Некоторые значения функции отображения единичного квадрата  для последнего выражения приведены в табл. 4.2.
для последнего выражения приведены в табл. 4.2.
Таблица 4.2
Некоторые координаты отображения единичного квадрата с помощью функции 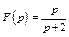
| A | B | C | D | |
| σ | 0.5 | 0.5 | – 0.5 | – 0.5 |
| ω | 0.5 | – 0.5 | – 0.5 | 0.5 |
| u | 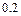
| 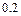
| 
| 
|
| v | 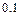
| 
| 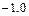
| 
|
Графическое представление этого отображения приведено на рис. 4.7.
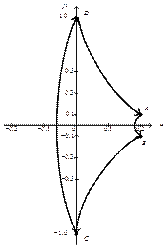
Рис. 4.7. Отображение квадратного единичного контура с помощью функции 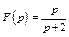
Построенный контур охватывает нуль отображающей функции 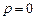 , но не охватывает полюс
, но не охватывает полюс  .
.
■
В общем случае любая дробно-рациональная функция 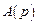 с конечным числом нулей и полюсов может быть представлена в виде
с конечным числом нулей и полюсов может быть представлена в виде
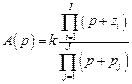 ,
,
где zi – нули, а pj – полюсы функции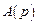 . Рассматривая
. Рассматривая  в качестве характеристического полинома разомкнутой системы, т.е. полагая
в качестве характеристического полинома разомкнутой системы, т.е. полагая 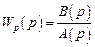 , из (4.10), (4.11) и последнего выражения получим, что
, из (4.10), (4.11) и последнего выражения получим, что

и, следовательно, полюсы 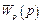 совпадают с полюсами
совпадают с полюсами  .
.
Охваты полюсов и нулей функции на
на  -плоскости обычно связываются с охватом начала координат
-плоскости обычно связываются с охватом начала координат -плоскости при помощи теоремы Коши, называемой принципом аргумента: если контур
-плоскости при помощи теоремы Коши, называемой принципом аргумента: если контур 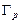 на
на  -плоскости при движении по нему по часовой стрелке охватывает Z нулей и P полюсов функции
-плоскости при движении по нему по часовой стрелке охватывает Z нулей и P полюсов функции  , то соответствующий контур
, то соответствующий контур  на
на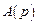 -плоскости охватывает начало координат
-плоскости охватывает начало координат 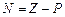 раз.
раз.
Для рассмотренных выше примеров имеем
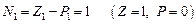
и
 .
.
Теорему Коши легче понять, если рассматривать изменение аргумента функции 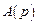 при движении по контуру
при движении по контуру 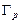 в направлении по часовой стрелке. Рассмотрим в качестве примера функцию
в направлении по часовой стрелке. Рассмотрим в качестве примера функцию
 ,
,
где  – нули, а
– нули, а  – полюсы.
– полюсы.
Это выражение можно представить в полярных координатах в виде

Выберем на  -плоскости некоторый контур
-плоскости некоторый контур 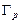 , как показано на рис. 4.8, а.
, как показано на рис. 4.8, а.

Рис. 4.8. Вычисление изменения аргумента:
а – контур на p-плоскости, б – контур на  -плоскости
-плоскости
Определим изменение аргумента каждого вектора при изменении переменной p вдоль этого контура. Ясно, что суммарное изменение каждого аргумента при полном обходе контура будет равно нулю. Однако при этом векторы, соответствующие внешним по отношению к контуру нулям р 1 , р 2 и полюсу z 2, повернутся на некоторый угол и возвратятся в начальное состояние, а вектор, соответствующий нулю z 1 (он находится внутри контура 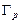 !) совершит полный оборот (результирующее изменение аргумента
!) совершит полный оборот (результирующее изменение аргумента будет равно 360˚).
будет равно 360˚).
Если бы внутри контура 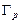 находилось Z нулей, то результирующее изменение аргумента
находилось Z нулей, то результирующее изменение аргумента 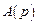 было бы равно
было бы равно  радиан, а если бы Z нулей и P полюсов – то
радиан, а если бы Z нулей и P полюсов – то 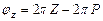 радиан. Поскольку на
радиан. Поскольку на  -плоскости вектор
-плоскости вектор  , конец которого находится на контуре
, конец которого находится на контуре  , повернется на угол
, повернется на угол  или
или 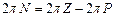 (рис. 4.8, б), то число охватов вектором начала координат будет равно
(рис. 4.8, б), то число охватов вектором начала координат будет равно 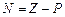 . Для
. Для 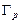 - и
- и  -контуров, приведенных на рис. 4.9, число охватов равно
-контуров, приведенных на рис. 4.9, число охватов равно
 .
.

Рис. 4.9. Соответствие числа нулей и полюсов числу охватов начала координат
Таким образом, характер размещения нулей и полюсов на p-плоскости функции 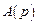 здесь определяется характером изменения аргумента этой функции на
здесь определяется характером изменения аргумента этой функции на 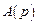 -плоскости.
-плоскости.
Критерий Михайлова. Применение принципа аргумента к характеристическому полиному A (p) разомкнутой системы при использовании в качестве контура мнимой оси (p = jω), замкнутой полуокружностью бесконечного радиуса определяет критерий Михайлова. Он позволяет судить об устойчивости замкнутой системы управления по ее характеристическому полиному.
Пусть дан характеристический полином разомкнутой системы
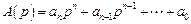 .
.
Представим его в виде
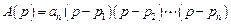 ,
,
где pi – корни полинома 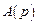 .
.
Положим теперь 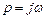 , тогда
, тогда
 .
.
Рассмотрим графическое представление сомножителей  на комплексной плоскости, показанное на рис. 4.10.
на комплексной плоскости, показанное на рис. 4.10.
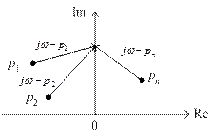
Рис. 4.10. Графическое представление комплексных чисел
Начала векторов находятся в точках pi, а концы – на мнимой оси в точке jω.
Аргумент комплексного числа A (jω) равен
 ,
,
а его изменение с изменением ω от – ∞ до ∞ есть
 .
.
Для определения изменения аргумента необходимо подсчитать сумму изменений аргументов двучленов 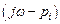 . Значения слагаемых этой суммы определяется в зависимости от расположения корней
. Значения слагаемых этой суммы определяется в зависимости от расположения корней 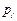 . Если корень лежит в левой полуплоскости, то при изменении ω от – ∞ до ∞ конец вектора
. Если корень лежит в левой полуплоскости, то при изменении ω от – ∞ до ∞ конец вектора 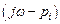 скользит вдоль мнимой оси снизу вверх, поворачиваясь против часовой стрелки на 180˚ (см. рис. 4.10), при этом изменение аргумента равно
скользит вдоль мнимой оси снизу вверх, поворачиваясь против часовой стрелки на 180˚ (см. рис. 4.10), при этом изменение аргумента равно
 .
.
Если корень лежит в правой полуплоскости, то при изменении ω от – ∞ до ∞ конец вектора 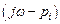 скользит вдоль мнимой оси сверху вниз, поворачиваясь по часовой стрелке на –180˚, при этом изменение аргумента равно
скользит вдоль мнимой оси сверху вниз, поворачиваясь по часовой стрелке на –180˚, при этом изменение аргумента равно
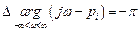 .
.
Если уравнение 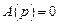 из своих n корней имеет l корней в правой полуплоскости и n – l корней в левой полуплоскости, то
из своих n корней имеет l корней в правой полуплоскости и n – l корней в левой полуплоскости, то
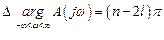 .
.
Последнее выражение и есть запись принципа аргумента для характеристического полинома 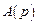 .
.
Для устойчивости системы управления необходимо и достаточно, чтобы число правых корней l было равно нулю, при этом
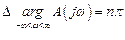
и аргумент  с увеличением
с увеличением  будет монотонно возрастать.
будет монотонно возрастать.
Графическим представлением критерия устойчивости Михайлова является годограф Михайлова. Для устойчивости системы управления необходимо и достаточно, чтобы годограф характеристического полинома  , начинаясь при ω = 0 на действительной оси, с ростом ω до ∞ обходил последовательно в положительном направлении n квадрантов, где n – порядок характеристического полинома.
, начинаясь при ω = 0 на действительной оси, с ростом ω до ∞ обходил последовательно в положительном направлении n квадрантов, где n – порядок характеристического полинома.
Примеры годографов Михайлова для устойчивых систем приведены на рис. 4.11, а, неустойчивых – на рис. 4.11, б.
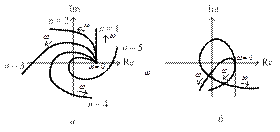
Рис. 4.11. Примеры годографов Михайлова
для устойчивых (а) и неустойчивых (б) систем
|
|
Дата добавления: 2014-01-15; Просмотров: 1407; Нарушение авторских прав?; Мы поможем в написании вашей работы!