
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тригонометрична форма запису комплексних чисел
План.
План.
61. Екстремум функції двох змінних (*).
62. Знаходження найбільшого та найменшого значень неперервної функції на замкненій обмеженій множині. (*).
63. Умовний екстремум для функції двох змінних. (*).
21.1 Екстремум функції двох змінних.
Означення. Нехай функція 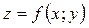 визначена в деякому околі точки
визначена в деякому околі точки  і неперервна в цій точці. Якщо для всіх точок
і неперервна в цій точці. Якщо для всіх точок  цього околу виконується нерівність
цього околу виконується нерівність 
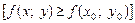 , тоді ця точка
, тоді ця точка 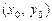 називається точкою максимуму (мінімуму) функції
називається точкою максимуму (мінімуму) функції 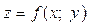 .
.
Точки максимуму й мінімуму називаються точками екстремуму.
Теорема (необхідна умова екстремуму). Якщо функція 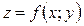 має екстремум у точці (x0; y0), тоді в цій точці частинні похідні
має екстремум у точці (x0; y0), тоді в цій точці частинні похідні 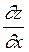 і
і 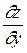 або дорівнюють нулю, або хоча б одна з них не існує.
або дорівнюють нулю, або хоча б одна з них не існує.
Теорема (достатня умова екстремуму). Нехай функція 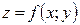 має у точці (x0; y0) неперервні частинні похідні першого й другого порядку, причому
має у точці (x0; y0) неперервні частинні похідні першого й другого порядку, причому  та
та  , а також
, а також 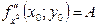 ,
, 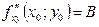 ,
, 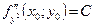 . Якщо:
. Якщо:
1) 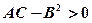 і
і 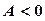 , тоді (x0; y0) точка максимуму функції
, тоді (x0; y0) точка максимуму функції 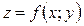 ;
;
2) 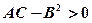 і
і  , тоді (x0; y0) точка мінімуму функції
, тоді (x0; y0) точка мінімуму функції 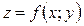 ;
;
3) 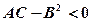 , тоді в точці (x0; y0) немає екстремуму.
, тоді в точці (x0; y0) немає екстремуму.
4)  , тоді потрібні додаткові дослідження.
, тоді потрібні додаткові дослідження.
Алгоритм дослідження функції 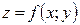 на екстремум:
на екстремум:
1. Знайти перші частинні похідні  та
та 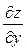 .
.
2. Знайти стаціонарні точки, тобто точки, в яких 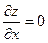 ,
, 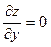 .
.
3. Знайти частинні похідні другого порядку  ,
, 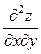 ,
, 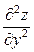 .
.
4. Обчислити значення частинних похідних другого порядку в стаціонарних точках.
5. Для кожної стаціонарної точки знайти  і зробити висновки.
і зробити висновки.
Приклад. Розглянемо функцію 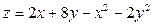 .
.
1. Знайдемо 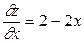 ,
,  .
.
2. Необхідна умова існування екстремуму полягає в тому, що
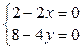 .
.
Розв’язком цієї системи є точка з координатами x=1, y=2.
Таким чином, у точці (1; 2) функція може мати екстремум.
3. Знайдемо похідні другого порядку 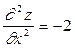 ,
, 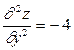 ,
,  , звідки дістаємо, що
, звідки дістаємо, що  .
.
4. Екстремум у точці (1; 2) існує – це максимум, бо 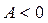 .
.
21.2 Знаходження найбільшого та найменшого значень неперервної функції на замкненій обмеженій множині.
Функція, що неперервна на замкненій обмеженій множині D, досягає на ній найбільшого та найменшого значень. Цих значень вона може набувати як у внутрішніх точках множини D (кожна така точка є точкою екстремуму функції, у цій точці перші частинні похідні дорівнюють нулю або не існують), так і на її межі, тобто необхідне спеціальне дослідження межових точок множини D.
Приклад. Знайти найбільше та найменше значення функції 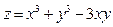 в області, обмеженій прямими x = -1, x = 2, y = -1, y = 3-x.
в області, обмеженій прямими x = -1, x = 2, y = -1, y = 3-x.

| 1. Дослідимо поводження функції всередині області KLMP. Знайдемо перші частинні похідні функції 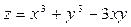 : :
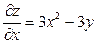 , , 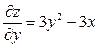 .
Прирівнявши їх до нуля, дістанемо стаціонарні точки .
Прирівнявши їх до нуля, дістанемо стаціонарні точки 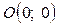 та та 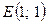 .
2. Дослідимо поводження функції на межі області. Відрізок .
2. Дослідимо поводження функції на межі області. Відрізок 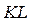 має рівняння має рівняння 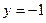 , , 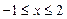 . Підставивши . Підставивши 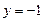 у задану функцію, дістанемо у задану функцію, дістанемо 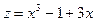 . Треба знайти найбільше та найменше значення цієї функції на відрізку . Треба знайти найбільше та найменше значення цієї функції на відрізку  . .
|
Маємо 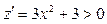 , отже, функція зростає і тому досягає найбільшого значення на кінцях відрізка, тобто в точках
, отже, функція зростає і тому досягає найбільшого значення на кінцях відрізка, тобто в точках 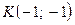 і L(2; -1).
і L(2; -1).
Відрізок  має рівняння
має рівняння 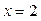 ,
, 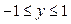 . Підставивши
. Підставивши 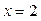 у задану функцію, дістанемо функцію z як функцію від змінної у:
у задану функцію, дістанемо функцію z як функцію від змінної у: 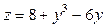 . Маємо
. Маємо 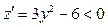 на відрізку
на відрізку 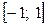 .
.
Отже, функція 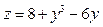 досягає найбільшого та найменшого значень на кінцях відрізка, тобто в точках L(2; -1 і M(2; 1).
досягає найбільшого та найменшого значень на кінцях відрізка, тобто в точках L(2; -1 і M(2; 1).
Відрізок 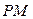 має рівняння
має рівняння 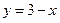 ,
,  . Підставивши
. Підставивши 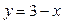 у задану функцію, дістанемо функцію z як функцію від змінної х:
у задану функцію, дістанемо функцію z як функцію від змінної х: 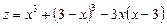 , тобто
, тобто 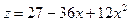 . Маємо
. Маємо  , звідки
, звідки 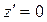 при
при 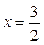 . Отже, на відрізку
. Отже, на відрізку 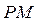 функція може досягати найбільшого та найменшого значень у точках M(2; 1),
функція може досягати найбільшого та найменшого значень у точках M(2; 1), 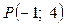 та
та 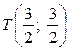 .
.
Відрізок 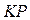 має рівняння
має рівняння  ,
, 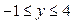 . Підставивши
. Підставивши 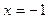 у задану функцію, дістанемо
у задану функцію, дістанемо 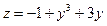 . Маємо
. Маємо 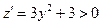 , отже, функція досягає найбільшого та найменшого значень на кінцях відрізка, тобто в точках
, отже, функція досягає найбільшого та найменшого значень на кінцях відрізка, тобто в точках 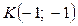 ,
,  .
.
Таким чином, функція  може досягти найбільшого та найменшого значень тільки в таких точках:
може досягти найбільшого та найменшого значень тільки в таких точках: 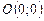 ,
, 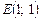 ,
, 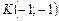 ,
, 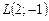 ,
, 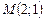 ,
, 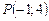 ,
,  .
.
Знаходимо  ,
,  ,
, 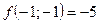 ,
, 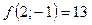 ,
, 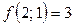 ,
, 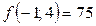 ,
,  .
.
Отже,  , і це значення досягається в точці (-1; -1),
, і це значення досягається в точці (-1; -1), 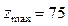 , і це значення досягається в точці (-1; 4).
, і це значення досягається в точці (-1; 4).
21.3 Умовний екстремум для функції двох змінних.
Нехай на відкритій множині  задано функцію
задано функцію 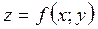 , змінні якої задовольняють рівнянню
, змінні якої задовольняють рівнянню 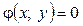
Рівняння 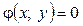 називають рівнянням зв’язку.
називають рівнянням зв’язку.
Точку  називають точкою умовного строгого максимуму функції
називають точкою умовного строгого максимуму функції 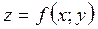 відносно рівняння зв’язку
відносно рівняння зв’язку 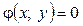 , якщо існує такий окіл точки
, якщо існує такий окіл точки 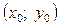 , для всіх точок якого
, для всіх точок якого 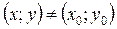 , що задовольняють рівняння зв’язку, справджується нерівність
, що задовольняють рівняння зв’язку, справджується нерівність  .
.
Якщо за таких умов виконується 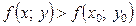 , тоді точку
, тоді точку 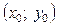 називають точкою умовного строгого мінімуму функції
називають точкою умовного строгого мінімуму функції 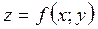 при обмеженнях
при обмеженнях 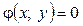 .
.
Аналогічно вводяться поняття нестрогого умовного екстремуму.
Точки умовного максимуму та мінімуму називають точками умовного екстремуму. Умовний екстремум інколи називають відносним екстремумом.
Якщо рівняння зв’язку 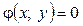 можна розв’язати відносно змінної y, наприклад,
можна розв’язати відносно змінної y, наприклад, 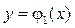 , тоді дослідження функції
, тоді дослідження функції 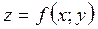 на умовний екстремум при обмеженні
на умовний екстремум при обмеженні 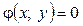 зводиться до дослідження на звичайний екстремум функції однієї змінної x:
зводиться до дослідження на звичайний екстремум функції однієї змінної x:
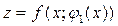 .
.
Приклад. Знайти умовний екстремум функції z = xy відносно рівняння зв’язку x + y = 6.
Розв’яжемо рівняння зв’язку відносно змінної y:
y= 6 – x

| Підставимо знайдене значення y у вираз для z та зведемо задачу до дослідження на безумовний екстремум функції z = x(6 - x),
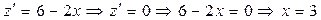 .
Таким чином, задана функція має умовний екстремум у точці (3; 3). .
Таким чином, задана функція має умовний екстремум у точці (3; 3).
|
Контрольні запитання.
1. Які повинні виконуватися умови, щоб функції двох змінних мала екстремум в певній точці. (*)?
2. На прикладі поясніть застосування алгоритму знаходження екстремума функції двох змінних (*).
3. Що назівають умовним екстремумом для функції двох змінних (*)?
|
Лекція 22. Комплексні числа
1. Означення комплексного числа (*).
2. Дії над комплексними числами (**).
3. Тригонометрична форма комплексного числа (**).
4. Дії з комплексними числами в тригонометричній формі. Формула Муавра (**).
5. Корінь n- го ступіня з комплексного числа (**).
6. Формула Ейлера (*).
22.1 Означення комплексного числа і уявної одиниці
Число a + bί, де a,b – будь-які дійсні числа, ί – уявна одиниця, називається комплексним числом (a – дійсна частина, b – уявна частина комплексного числа, а ί – коефіцієнт при уявній частині).
Число, квадрат якого дорівнює 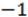 , позначають літерою ί – називають уявною одиницею (ί – перша буква латинського слова imaginarius – уявний).
, позначають літерою ί – називають уявною одиницею (ί – перша буква латинського слова imaginarius – уявний).
Тобто, для символу виконується рівність:
ί 2 = 1
Означення: з апис a + bί називають алгебраїчною формою комплексного числа.
Часто комплексне число позначають літерою Z і записують Z = a + bi.
Комплексні числа – це розширення числової системи дійсних чисел. Позначаються вони літерою С. Множина дійсних чисел є частиною (підмножиною) множини комплексних чисел.
Означення: числа a + bί і a - bί, дійсні частини яких рівні, а коефіцієнти при уявих частинах рівні за модулем, але протилежні за знаком, називають спряженими. Можна сказати простіше: числа a + bί і a - bί, які відрізняються лише знаком уявної частини, називають спряженими.
Означення: два числа a + bί та -a - bί, сумма яких дорівнює 0, називають протилежними.
У множині дійсних чисел справедлива рівність a + 0 = a. У множині комплексних чисел нулем є число 0 + 0ί. Справді, яке б не було число, справедлива рівність
(a + b ί) + (0+0 ί) = (a +0) + (b +0) ί = a + b ί
22.2 Дії над комплексними числами.
Означення: сумою двох комплексних чисел a + bί і c + dί називається комплексне число (a + c) + (b + d)ί.
Приклади. Виконати додавання комплексних чисел:
1) (3+2ί) + (-1-5ί) = (3-1) + (2-5)ί = 2-3ί
2) (4-5ί) + (2-ί) = (4+2) + (-5-1)ί = 6-6ί
3) (2+3ί) + (6-3ί) = (2+6) + (3-3)ί= 8
4) (10 – 3ί) + (-10+3ί) = (10-10) + (-3+3)ί = 0
Означення. Різницею двох комплексних чисел Z 1 = a + bί і Z 2 = c + dί називається таке комплексне число Z = (а-с)+(b-d)ί.
Приклади: Виконати віднімання комплексних чисел.
1) (3+4ί) – (1+2ί) = (3-1) + (4-2)ί = 2 + 2ί
2) (-5+2ί) – (2+ί) = (-5-2) + (2-1)ί = -7+ί
3) (6+7ί) – (6-5ί) = (6-6) + (7+5)ί = 12ί
Означення. Добутком двох комплексних чисел Z 1 = a + bί і Z 2 = c + dί називається комплексне число z = (ac - bd) + (ad + bc)ί.
Приклади: Виконити множення комплексних чисел.
1) (4-5ί)(3+2ί) = 12+8ί -15ί -10ί²= 12+10-7ί =22-7ί
2) (2-ί)(-5) = -10+5ί
3) (-4-3ί)(-6ί) = -18+24ί
Означення. Часткою комплексних чисел Z 1 = a + bί і Z 2 = c + dί називається таке комплексне число:
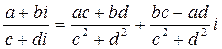
Приклади. Знайти частку комплексних чисел.
1) (2+5ί)/(3-2ί) = (2+5ί)(3+2ί)/(3-2ί)(3+2ί) = (-4+19ί)/13 = -4/13+19ί/13
2) (3+ί)/ί = (3+ί)(-ί)/ί = 1-3ί
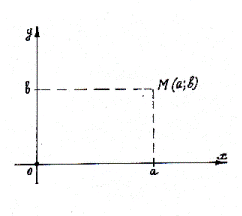
Кожному комплексному числу a + bί поставимо у відповідність точку М (a;b) координатної площини, тобто точку, абсциса якої дорівнює дійсній частині комплексного числа, а ордината – коефіцієнту уявной частини. Кожній точці М (a;b) координатної площини поставимо у відповідність комплексне число.
Очевидно, що така відповідність є взаємно однозначною. Вона дає можливість інтерпретувати комплексні числа як точки деякої площини, на якій вібрано систему координат. Координатну площину називають при цьому комплексною, вісь абсцис – дійсною віссю, бо на ній розміщені точки, що відповідають комплексним числам a + 0ί, тобто відповідають дійсним числам. Вісь ординат називають уявною віссю – на ній лежать точки, які відповідають уявним комплексним числам 0+ bί.
 Модулем комплексного числа Z = a + bί називається число: r =
Модулем комплексного числа Z = a + bί називається число: r =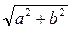 . Позначимо α кут, який утворює вектор
. Позначимо α кут, який утворює вектор 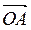 з додатним напрямом осі Ох. Числове значення кута α, виміряного в радіанах, називається аргументом комплексного числа a + bί. Значення аргументу, взяте в межах першого кола, тобто від 0 до 2π, називається головним. Головне значення аргументу комплексного числа можна визначити з рівності tg α = b/a. Справді, за знаками a i b можна встановити, в якій четверті міститься кут α, і за величиною tg α, використовуючи таблиці, знайти величину кута α.
з додатним напрямом осі Ох. Числове значення кута α, виміряного в радіанах, називається аргументом комплексного числа a + bί. Значення аргументу, взяте в межах першого кола, тобто від 0 до 2π, називається головним. Головне значення аргументу комплексного числа можна визначити з рівності tg α = b/a. Справді, за знаками a i b можна встановити, в якій четверті міститься кут α, і за величиною tg α, використовуючи таблиці, знайти величину кута α.
Вираз Z = r cos α + ί r sin α = r (cos α + ί sin α) називається тригонометричною формою комплексного числа.
Приклад. Подати в тригонометричній формі число – 3 + 2 і.
Маємо: 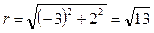 ,
, 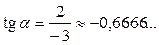
Тангенс від’ємний, отже, кут  треба шукати в ІІ або IV чверті.
треба шукати в ІІ або IV чверті.
Далі: а = – 3 і b = 2 синус буде додатний, а косинус — від’ємний, тобто  буде кутом ІІ чверті. За таблицями знаходимо:
буде кутом ІІ чверті. За таблицями знаходимо:  = 146° 18¢, а тому:
= 146° 18¢, а тому:

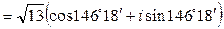 .
.
22.4 Дії з комплексними числами в тригонометричній формі. Формула Муавра.
Якщо задані два числа:
Z1 = r1 (cos α1 + + ί sin α1) і Z2 = r2 (cos α2 + + ί sin α2)
Тоді: Z1 Z2 = r1r2 (cos (α1 + α2) + ί sin (α1 + α2));
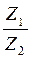 =
= 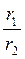 (cos (α1 – α2) + ί sin (α1 – α2)).
(cos (α1 – α2) + ί sin (α1 – α2)).
При будь – якому натуральному n:
Z n = (cos α + ί sin α) n = cos nα + ί sin nα.
Приклад.
 і
і 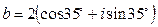 .
.
Тоді: 
a=12(cos55°+i sin55°) і b=3(cos35°+ +i sin 35°).
Тоді 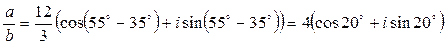
Знайдемо куб число a = 2 (cos 20° + i sin 20°).
Маємо:

 .
.
22.5 Корінь n -го ступеня з комплексного числа.
Корінь n – го ступеня з числа Z =r (cos α + ί sin α) обчислюють за формулою
ωk =
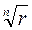 (cos
(cos 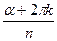 + ί sin
+ ί sin 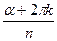 ), де k – ціле число.
), де k – ціле число.
Підставляючи замість k значення 0, 1, 2… n – 1, дістанемо n різних значень кореня.
|
|
Дата добавления: 2014-01-15; Просмотров: 679; Нарушение авторских прав?; Мы поможем в написании вашей работы!
