Функции от одного случайного аргумента

Функции от случайных величин

Рассмотренные нами основные законы распределения случайных величин, в чистом виде, встречаются не так уж и часто. Область их применения можно значительно расширить, если случайные величины, описывающие случайные явления, выражать через функцию от других случайных величин или хотя бы, через неслучайную функцию одной случайной величины.

Пусть, например, нас интересует распределение случайной величины h, которая связана функционально со случайной величиной x по формуле h = j (x), для которой функция распределения F_x (x) известна. Задача состоит в нахождении функции распределения случайной величины h, где

, .

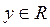В некоторых случаях решение задачи может быть получено из здравого смысла, которое должно быть проверено формально.

Пример. Дискретная случайная величина x задана законом распределения

x	-1
р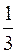

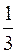
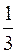
Построить закон распределения случайной величины .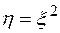

Решение. Случайная величина h неотрицательна и, очевидно, принимает два значения. Закон распределения имеет вид:

h
р

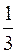
Замечание. Законы распределения для случайных величин и x × x различны. Это означает, что ¹ x × x. В самом деле, слева мы над случайной величиной произвели неслучайную математическую операцию: возведение в квадрат и получили два значения h: 0, 1, а справа стоит произведение двух случайных величин. Эта случайная величина h, для которой имеем три различных значения. Закон распределения имеет вид:

h=x×x	-1
р

Рассмотренный пример демонстрирует подход построения закона распределения для функции одного случайного аргумента дискретной случайной величины.

Проведем построение функции распределения случайной величины h, являющейся функцией случайной величины x, с заданным распределением F_x (х).

Определение. Пусть функция у = j (х) строго монотонна в области (х Î C)&(у Î У), где символ «&» читается как «и».

Функция j ^-1 называется обратной к j, если она определена на множестве У и

.

Если j (х) возрастающая и j (х)< у, то х < j ^-1(у), если j (х) убывающая, то .

Рассмотрим случайную величину x с функцией распределения F_x (х) и плотностью r_x (х). Пусть у = j (х) строго монотонная и дифференцируемая, вместе со своей обратной, функция. Пусть случайная величина h = j (x). Требуется найти F_h (у) и r_h (у), где у Î У - значения случайной величины h.

По определению, имеем

F_h (у) = Р { h < у }, тогда, если j (х) возрастающая, то

Р { j (x)< у } = Р { x < j ^-1(у)}.

Отсюда

F_h (у) = F_x (j ^-1(у)),

или

.

Для плотности получаем:

. (42)

Если j (х) - убывающая, то

, но тогда .

Отсюда

.

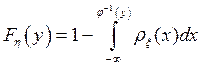Для плотности, аналогично, получаем

(43)

Учитывая, что производная убывающей функции отрицательна, правая часть (43) положительна.

Объединяя (42) и (43), получаем:

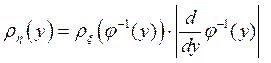(44)

Пример. Пусть случайная величина x имеет функцию распределения F_x (х), а случайная величина h = ax + b, a, b Î R.

Найти F_h (y) и r_h (y), где у – значение случайной величины h из области У.

Решение. Если a > 0, функция у = aх + b возрастающая, тогда

,

отсюда

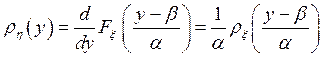
Если a < 0, то у = aх + b - убывающая, тогда

,

отсюда

.

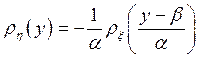Учитывая (44), для плотности получаекм

.

Пример. Пусть случайная величина x имеет экспоненциальное распределение , х >0. Найти распределение случайной величины h = е^-bx, b >0.

Решение. Имеем

F _h(y) = P { h < y }= P { e^-bx < y }.

Если у < 0, то событие невозможно, тогда F_h (y) = 0. Если у >1, то событие - достоверное, тогда F_h (y) = 1.

Пусть теперь у Î(0,1), тогда

.

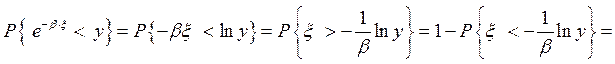
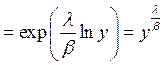Таким образом, с учетом того, что имеем,

Дата добавления: 2014-01-15