Імовірнісна модель фінансових потоків та їх стабілізація

Досліджується країна або її регіон з 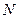суб’єктами. В початковий момент в кожному з 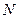міст знаходиться певна грошова маса, яка далі починає циркулювати між містами. Якщо таку ситуацію не контролювати, то може бути створений дисбаланс у грошовій ситуації регіону, який буде важко ліквідувати.

а. Потокова модель з втручанням у грошову ситуацію.

Вектор 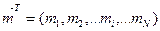визначає кількість грошей, що перебувають в певний момент часу у місті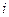 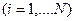. Вектор управління 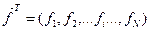задає кількість грошей, яку уряд віднімає чи додає місту :

.

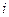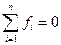Вектор 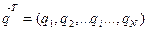задає кількість грошей, яка має бути у кожному місті в умовах стабільності.

Нехай 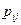– частка грошей, що переходить з міста 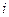в місто 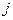за певний час.

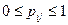можна розглядати як ймовірність відповідного переходу. Ймовірність вилучення грошей з обігу (вклади в банках або зберігаються в дома) у місті 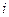позначимо.

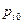Загальну грошову ситуацію можна описати матрицею .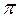

Маємо матрицю одно крокового переходу з одним поглинальним станом .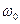

З матриці 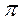легко визначити матрицю 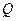. Тоді вектор 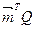дасть розподіл грошей через один крок (проміжок часу), 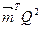– через два кроки, 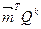– через 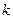кроків.

Вплив уряду на грошову ситуацію на 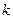кроці визначається вектором:

.

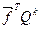Тоді за n кроків ситуація 3 розподілом грошей буде визначатися вектором:

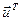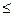
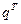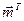
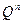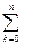
(n)(n) = +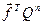(2.15)

де 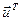(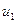k) = ((k), 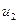(k), … 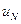(k)) – вектор, якого задають бажаний розподіл грошової маси.

Для поглинальних ланцюгів Маркова.

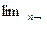
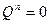
Тому у рівнянні (2.15) основне значення має другий член правої частини

=

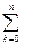
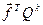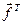
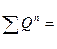
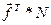
Таким чином з (2.15) випливає

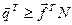, або 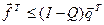(2.16)

Для перевірки прийнятності вектора 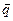з рівностей (2.15) та (2.16) отримуємо

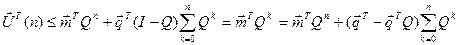
Якщо враховувати, що компоненти всіх векторів, які фігурують в останньому рівнянні повинні бути додатними, то однією з умов прийнятності вектора 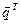може бути забезпечення невід’ємності виразу, що стоїть у дужках, тобто:

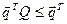(2.17)

Взагалі, дану модель можна використовувати для розв’язування таких задач:

1. Знаходження вектора 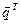(n) при заданих векторах 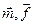та матрицю

2. Знаходження вектора 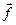при заданих векторах 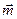,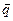та матрицю

При цьому можна використати і інші, крім (2.17) критерії прийнятності вектора :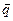

(2.18)

и також умову, щоб сума абсолютних величин компонентів вектора 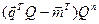не перевищувала найменшого компонента вектора .

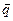Приклад 2.7

1. Потонова модель між трьома містами характеризується матрицею:

,

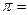
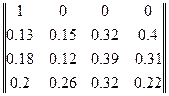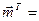(10; 4; 16),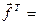(-2; 8; -6)

а) дати економічну інтерпретацію компонентам задають матриці та векторів;

б) знайти компоненти вектора 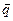та дати їм скорочену інтерпретацію.

,

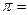
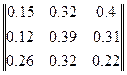(0,735; 15,746; 0,326)

2. За даною матрицею:

,

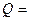
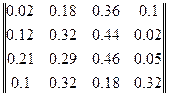с вектором 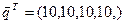, що задає бажаний розподіл грошей між чотирма містами, визначити вектор 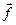, що визначає грошову політику регіону. Перевірити на прийнятність вектори 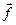та .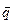

Маємо:

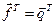(I-Q),

.

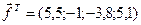Як видно вектор 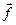не задовольняє умов:

.

Для перевірки прийнятності вектора 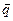знаходимо:

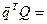(4,5; 11; 14,4; 4,9).

Як видно за критерієм (2.17) вектор 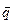не є прийнятним. Можна перевірити прийнятність вектора 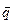за критерієм (2.18).

6. В регулярних ланцюгах Маркова поглинальні стани відсутні.

Взагалі: якщо існує таке число k, при якому з будь якого стану системи перехід в будь який інший стан можливий за k кроків, то відповідний процес називається регулярним ланцюгом Маркова.

Для регулярних ланцюгів Маркова в матриці однокрокового переходу через k кроків будуть відсутні нульові елементи.

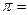
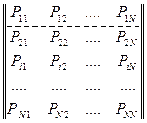
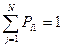, (2.19)

Якщо матриця задана, то для регулярних ланцюгів Маркова можна відмітити такі властивості:

а) для будь-якого вектора початкових станів 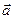виконується співвідношення:

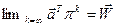,(2.20)

б) 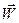- вектор стаціонарних (фінальних) ймовірностей з властивостями:

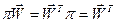, (2.21)

,

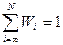в) існує 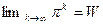(2.22),

де W називається матрицею стаціонарних (фінальних) ймовірностей.

г) для регулярних ланцюгів Маркова довго тривале функціонування системи не залежить від початкового стану.

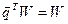(2.23),

.

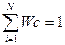Приклад 2.8

Задана матриця однокрокового переходу:

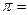
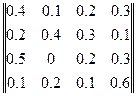
Знайти ймовірність перебування систем у стані , якщо в початковий момент вона перебуває у стані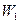

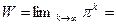
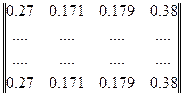
Для регулярних ланцюгів Маркова вводять фундаментальну матрицю

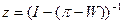
Для фундаментальної матриці z виконується співвідношення

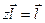(2.24)

Приклад 2.9

Для фундаментальної матриці, що визначається матрицею однокрокового переходу перевірити виконання рівності (2.24)

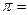
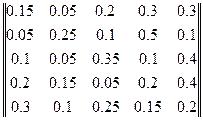
З допомогою фундаментальної матриці z можна визначити ряд головних характеристик регулярних ланцюгів Маркова:

а) Матриця середніх значень часу досягнення певного кінцевого стану з певного початкового стану:

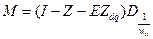(2.25)

E – матриця всі елементи якої дорівнюють одиниці;

Z_dq – матриця що містить діагональні елементи матриці Z, а решта елементів нулі;

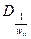- діагональна матриця з елементами 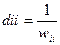, де 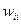діагональні елементи матриці W.

Приклад 2.10

Для даних прикладу 2.9 визначити елементи матриці M та дати їм економічне тлумачення.

б) Дисперсія часу першого досягнення стану:

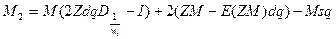(2.26),

де 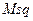отримана з матриці 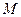шляхом піднесення її елементів до квадрату.

7. Розглянемо імовірну модель фінансових потоків із збереженням контрольованої урядом грошової маси.

У цьому випадку поглинальні стани відсутні і можна використовувати матрицю у вигляді (2.19).

Імовірність потоків моделі має вигляд:

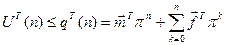(2.27)

При небажаному збільшенні кроків, маємо:

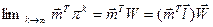(2.28)

Тобто, розподіл фінансів, незалежно від їхнього розподілу в початковий момент часу, здійснюється через достатньо великий проміжок часу пропорційно до вектора .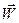

Дослідимо поведінки другого імена правової частини рівняння (2.27) при .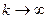

Оскільки:

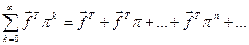, то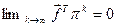– є умова скінченності для виразу (2.27).

Далі:

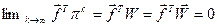, і, так як 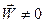, то.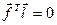

Тобто, для стабільності грошової ситуації при відсутності поглинальних станів, не потрібно залучати додаткові гроші, а лише перерозподіляти їх між регіонами.

Врахувавши отримані висновки і зробивши відповідні перетворення, встановлюємо, що:

,

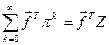а модель (2.27) набуває вигляду:

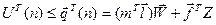(2.30)

При цьому на вектор накладаються певні обмеження, що випливають із встановлених раніше залежностей. Так, враховуючи, що:

; ; ; ,

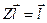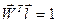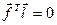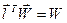з рівності (2.30) шляхом множення обох її частин на вектор справа отримаємо:

,

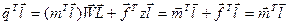тобто:

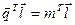(2.31)

Далі, помноживши ліву і праву частини рівності (2,30) на 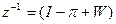і зробивши перетворення отримаємо:

,

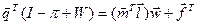Звідки:

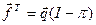
Приклад 2.11

Грошова ситуація регіону визначається матрицею:

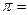
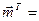(6, 4, 8, 2) 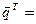(5, 5, 5, 5)

Визначити яка ситуація складається через чотири періоди часу.

Знаходимо:

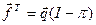= (0,5; -0,3 -0,6; 0,4)

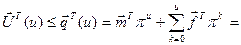(5,04; 5,024; 5,003; 4,933).

Дата добавления: 2014-01-11