Взаимное расположение линейных многообразий в пространстве

С помощью рангов соответствующих матриц можно определить взаимное расположение подпространств из некоторого пространства. При этом определённую пользу принесёт следующая теорема.

Теорема 7.14 Кронекера-Капели.

Система 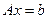совместна тогда и только тогда, когда .

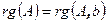Доказательство. Очевидно.

В качестве примера определим взаимное расположение двух линейных многообрази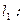й: и 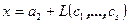(предполагается линейная независимость систем векторов 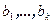и 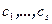). Рассмотрим две системы линейных уравнени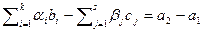й и 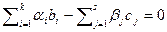. Положим и .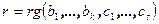

Совместность первой системы означает, что у линейных многообразий есть общая точка. Равенство рангов 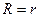является необходимым и достаточным условием совместности первой системы линейных уравнений (теорема Кронекера-Капели). Размерность пространства решений второй системы позволяет определить размерность пересечения линейных оболочек 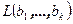и по формуле 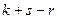. Этой информации достаточно для описания взаимного расположения линейных многообразий. В качестве примера приведём в таблицах все случаи взаимного расположения двух прямых, прямой и плоскости, двух плоскостей.

Две прямые (k=s=1)

r	R	примечание
		Прямые совпадают (есть общая точка и размерность пересечения равна 1)
		Прямые параллельны
		Прямые пересекаются в одной точке
		Прямые скрещиваются (нет общих точек и не параллельны)

Прямая и плоскость (k=1, s=2)

r	R	примечание
		Прямая лежит в плоскости
		Прямые параллельна плоскости
		Прямая пересекается с плоскостью в единственной точке
		Прямая и плоскость скрещиваются (нет общих точек и не параллельны)

Две плоскости (k=s=2)

r	R	примечание
		Плоскости совпадают
		Плоскости параллельны
		Плоскости пересекаются по прямой
		Плоскости скрещиваются, но имеют параллельные прямые
		Плоскости пересекаются в единственной точке
		Плоскости абсолютно скрещиваются (ни какие прямые одной плоскости не параллельны прямым другой плоскости)

Дата добавления: 2014-01-20