
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интервалы прогноза по линейному уравнению регрессии
|
|
|
|
Одной из центральных задач эконометрики является прогнозирование значений зависимой переменной при определенных значениях объясняющих переменных. Различают точечное и интервальное прогнозирование. При этом возможно предсказать условное математическое ожидание зависимой переменной (т.е. ср. значение), либо прогнозировать некоторое конкретное значение (т.е. индивидуальное).
Пусть имеется уравнение регрессии 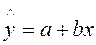 . Точечной оценкой М(У│Х=хр) =
. Точечной оценкой М(У│Х=хр) = 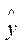 р =
р = 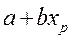 . Так как
. Так как 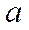 и
и 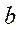 имеют нормальное распределение (в силу нормальности
имеют нормальное распределение (в силу нормальности  ), то
), то 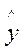 р является случайной величиной с нормальным распределением.
р является случайной величиной с нормальным распределением.
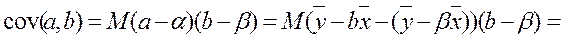
 ,
,
М(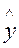 р) = М(
р) = М(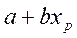 ) =
) = 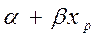
D(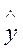 р) = D(
р) = D(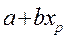 ) + D(
) + D(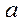 ) + xp2D(
) + xp2D(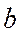 ) + 2cov(
) + 2cov(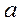 ,
,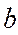 )xp =
)xp = 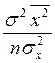 +
+
+ xp2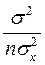 -2xp
-2xp
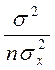 =
=  (
(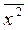 + xp2 - 2 xp
+ xp2 - 2 xp )│
)│ =
=
= 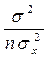 (
(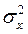 +
+ 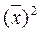 - 2 xp
- 2 xp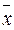 + xp2) =
+ xp2) = 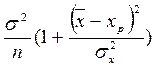 .
.
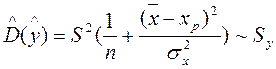 - стандартная ошибка положения линии регрессии. Так как она минимальна при хр =
- стандартная ошибка положения линии регрессии. Так как она минимальна при хр = 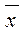 , то наилучший прогноз находится в центре области наблюдений и ухудшается по мере удаления от центра.
, то наилучший прогноз находится в центре области наблюдений и ухудшается по мере удаления от центра.
Случайная величина 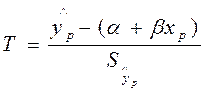 имеет распределение Стьюдента с (n-2) степенями свободы. Поэтому, задавая
имеет распределение Стьюдента с (n-2) степенями свободы. Поэтому, задавая 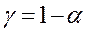 = Р(
= Р(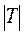 <tкр(
<tкр( , n-2)), можно построить доверительный интервал для М(У│Х = хр), то есть положения линии регрессии (рис. 1.): (
, n-2)), можно построить доверительный интервал для М(У│Х = хр), то есть положения линии регрессии (рис. 1.): ( )
)
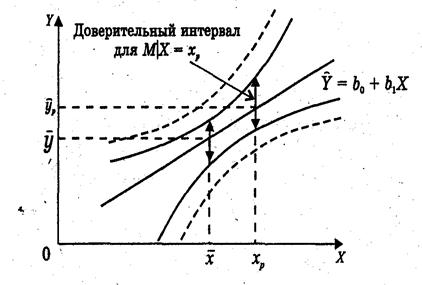
Рис. 1. Доверительные интервалы положения линии регрессии – сплошная линия и индивидуального значения – пунктирная линия.
Фактические значения у варьируются около среднего значения  р. Индивидуальные значения у могут отклоняться от
р. Индивидуальные значения у могут отклоняться от 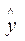 р на величину случайной ошибки
р на величину случайной ошибки  . Пусть yi - некоторое возможное значение у при хр. Если рассматривать yi как случайную величину У, а
. Пусть yi - некоторое возможное значение у при хр. Если рассматривать yi как случайную величину У, а 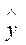 р – как случайную величину Ур, то можно отметить, что:
р – как случайную величину Ур, то можно отметить, что:
Y ~ N( , Yp ~ N(
, Yp ~ N(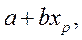
 ).
).
Y и Yp независимы и, следовательно, U = Y - Yp ~ N с параметрами
M(U) = 0; D(U) = 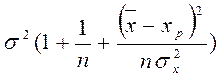 .
.
Значит 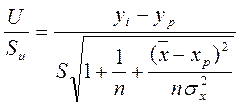 случайная величина, имеющая распределение Стьюдента с (n-2) степенями свободы. Аналогично строится доверительный интервал индивидуального значения.
случайная величина, имеющая распределение Стьюдента с (n-2) степенями свободы. Аналогично строится доверительный интервал индивидуального значения.
|
|
|
Пример. Стандартная ошибкасреднего расчетного значения
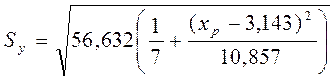 .
.
При 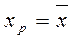 ,
, 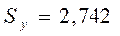 . При
. При 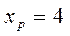 ,
, 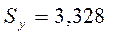 . Следовательно,
. Следовательно, 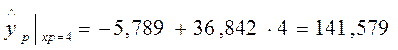 и, т.к.
и, т.к. 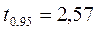 , то
, то  и
и
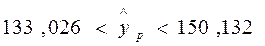 .
.
Стандартная ошибка индивидуального расчетного значения
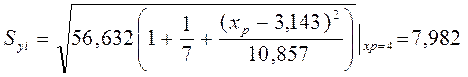 ,
,
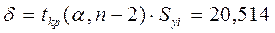 и
и 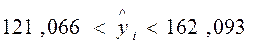 .
.
Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям. Поскольку  может быть как положительной, так и отрицательной величиной, ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
может быть как положительной, так и отрицательной величиной, ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Для того чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, находят среднюю ошибку аппроксимации как среднюю арифметическую простую.
 .
.
Допустимый предел 8 – 10 %, при котором подбор модели к исходным данным считается хорошим.
Возможно и другое определение средней ошибки аппроксимации:
 .
.
Рассчитаем среднюю ошибку аппроксимации для нашего примера.
| № | y | 
| 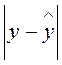
| 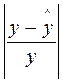
|
| 31,053 | 1,053 | 0,035 | ||
| 67,895 | 2,105 | 0,030 | ||
| 141,579 | 8,421 | 0,056 | ||
| 104,737 | 4,737 | 0,047 | ||
| 178,421 | 8,421 | 0,049 | ||
| 104,737 | 4,737 | 0,047 | ||
| 141,579 | 8,421 | 0,056 | ||
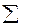
| 0,322 |
Окончательно получим: 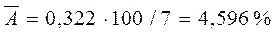 , что говорит о хорошем качестве уравнения.
, что говорит о хорошем качестве уравнения.
Выборочный коэффициент вариации определяется отношением выборочного среднего квадратического отклонения к выборочной средней, выраженным в процентах:
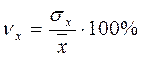 и
и 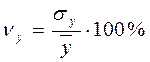 .
.
Коэффициент вариации – безразмерная величина, удобная для сравнения величин рассеивания двух и более выборок, имеющих разные размерности. Совокупность данных считается однородной и пригодной для использования МНК и вероятностных методов оценок статистических гипотез, если значение коэффициента вариации не превосходит 35 %.
Для нашего примера:
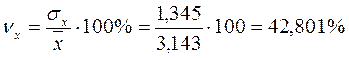 ,
,
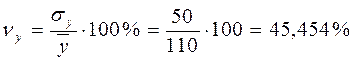 .
.
Пример. Фирма провела рекламную компанию. Через 10 недель фирма решила проанализировать эффективность этого вида рекламы, сопоставив недельные объемы продаж (у, тыс. руб.) с расходами на рекламу (х, тыс. руб.).
|
|
|
Полагая, что между переменными х и у имеет место линейная зависимость, определить выборочное уравнение регрессии.
| х | ||||||||||
| у |
Решение см. в Excel.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 553; Нарушение авторских прав?; Мы поможем в написании вашей работы!