
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Момент импульса
|
|
|
|
Опр.1.4.2. Моментом импульса материальной точки массой  , имеющей скорость
, имеющей скорость 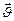 , относительно неподвижной точки О, называется векторное произведение радиуса-вектора материальной точки, проведенной из точки О, на импульс этой материальной точки
, относительно неподвижной точки О, называется векторное произведение радиуса-вектора материальной точки, проведенной из точки О, на импульс этой материальной точки 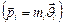 :
: 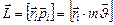 .
.
Опр.1.4.2. Моментом импульса механической системы относительно неподвижной точки О, называется вектор 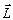 , равный геометрической сумме моментов импульса относительно той же точки всех материальных точек системы:
, равный геометрической сумме моментов импульса относительно той же точки всех материальных точек системы: 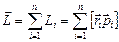 .
.
Опр.1.4.3. Моментом импульса материальной точки массой 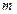 , имеющей скорость
, имеющей скорость 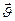 , относительно неподвижной оси наз. скалярная величина
, относительно неподвижной оси наз. скалярная величина , равная проекции на эту ось вектора момента импульса
, равная проекции на эту ось вектора момента импульса  , определенного относительно произвольной точки О данной оси. Значение момента импульса не зависит от положения точки О на оси z:
, определенного относительно произвольной точки О данной оси. Значение момента импульса не зависит от положения точки О на оси z:  .
.
Размерность  .
.
Момент силы и момент импульса связаны соотношением: 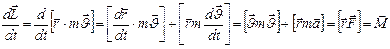 . (1.4.3.) Выражение в первой скобке равно нулю, т.к. равно нулю векторное произведение вектора на самого себя; во второй скобке
. (1.4.3.) Выражение в первой скобке равно нулю, т.к. равно нулю векторное произведение вектора на самого себя; во второй скобке  . В итоге
. В итоге  и
и 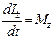 .
.
Момент импульса материальной точки  , (1.4.4)
, (1.4.4)
где 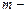 масса точки,
масса точки,  линейная скорость точки,
линейная скорость точки,  расстояние точки от оси, относительно которой определяется момент импульса,
расстояние точки от оси, относительно которой определяется момент импульса, 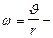 угловая скорость.
угловая скорость.
 Момент инерции.
Момент инерции.
Рассмотрим тело, вращающееся вокруг неподвижной оси с угловой скоростью. Его можно представить как совокупность материальных точек с массами  (одна из этих точек под номером
(одна из этих точек под номером  показана на рис.4). Момент импульса тела равен суммарному моменту импульса материальных точек (индекс
показана на рис.4). Момент импульса тела равен суммарному моменту импульса материальных точек (индекс 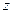 здесь и в дальнейшем опущен):
здесь и в дальнейшем опущен): 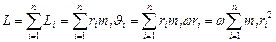 , (1.4.5.) т.к.
, (1.4.5.) т.к.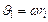 . Величина
. Величина характеризует распределение массы тела относительно оси вращения и называется моментом инерции тела.
характеризует распределение массы тела относительно оси вращения и называется моментом инерции тела.
Момент импульса и момент инерции связаны соотношением: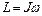 . (1.4.5.)
. (1.4.5.)
|
|
|
Опр.1.4.2. Моментом инерции тела относительно оси называется величина, являющаяся мерой инертности тела во вращательном движении вокруг этой оси и равная сумме произведений масс всех частиц тела на квадраты их расстояний от той же оси.
Размерность:  .
.
Момент инерции тела зависит только от формы тела и расположения масс в нем.
Момент инерции:
а) материальной точки массы 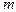 , находящейся на расстоянии
, находящейся на расстоянии  от оси вращения
от оси вращения 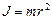 ; (1.4.4)
; (1.4.4)
б) системы материальных точек  , где
, где  расстояние элемента массы
расстояние элемента массы  от оси вращения. (1.4.6)
от оси вращения. (1.4.6)
в) твердого тела, которое можно рассматривать как механическую систему, масса  которой распределена по всему объему тела
которой распределена по всему объему тела  :
:  . (1.4.7)
. (1.4.7)
Если тело однородно, т.е. его плотность  одинакова по всему объему, то
одинакова по всему объему, то  и
и  . (1.4.8)
. (1.4.8)
Подсчет момента инерции тела относительно произвольной оси облегчается, если воспользоваться теоремой о параллельном переносе оси вращения (теореме Штейнера).
Теорема Штейнера: момент инерции тела  относительно произвольной оси
относительно произвольной оси 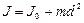 , (1.4.9)
, (1.4.9)
где 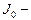 момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси,
момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси,  расстояние между осями,
расстояние между осями, 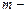 масса тела.
масса тела.
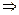 момент инерции тела
момент инерции тела  относительно оси, проходящей через его центр инерции, меньше момента инерции относительно любой параллельной ей оси.
относительно оси, проходящей через его центр инерции, меньше момента инерции относительно любой параллельной ей оси.
 Докажем эту теорему.
Докажем эту теорему.
|
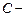 центр тяжести тела и
центр тяжести тела и  ось, проходящая через точку
ось, проходящая через точку 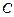 . Найдем момент инерции тела относительно некоторой произвольной оси
. Найдем момент инерции тела относительно некоторой произвольной оси 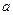 . Выберем малый элемент тела массой
. Выберем малый элемент тела массой 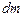 . Обозначим за
. Обозначим за  расстояние между
расстояние между 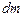 и осью
и осью  ,
,  расстояние между
расстояние между 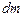 и осью
и осью 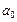 . По теореме косинусов
. По теореме косинусов  , откуда
, откуда  .
.
Выражение, стоящее под знаком третьего интеграла, есть абсцисса элемента 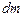 тела в системе координат с началом в центре масс тела и осью абсцисс, пересекающей оси
тела в системе координат с началом в центре масс тела и осью абсцисс, пересекающей оси  и
и 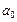 , и лежащей в перпендикулярной им плоскости. По определению центра масс
, и лежащей в перпендикулярной им плоскости. По определению центра масс , т.к. центр масс совпадает с началом координат. Т.о. справедливость соотношения доказана.
, т.к. центр масс совпадает с началом координат. Т.о. справедливость соотношения доказана.
|
|
|
Примеры расчета момента инерции некоторых тел правильной геометрической формы:
1) однородный тонкий стержень массой 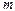 и длиной
и длиной  . Случаи:
. Случаи:
· ось проходит через центр тяжести стержня перпендикулярно к стержню.
Рассмотрим момент инерции участка АС. Масса малого элемента стержня  ,
,
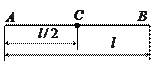 где
где 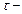 линейная плотность стержня,
линейная плотность стержня,  , получим
, получим
|
 .
.
Т.к.  , то момент инерции всего стержня
, то момент инерции всего стержня  и
и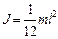 . (1.4.10)
. (1.4.10)
· ось проходит через конец стержня перпендикулярно к стержню.
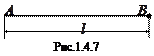 Аналогично предыдущему случаю
Аналогично предыдущему случаю
 , откуда
, откуда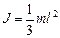 . (1.4.11)
. (1.4.11)
2) тонкие кольцо, обруч, тонкостенный цилиндр (труба) радиусом 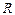 и массой
и массой 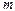 ; маховик радиусом
; маховик радиусом 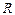 и массой
и массой 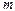 , распределенной по ободу. Ось проходит через центр перпендикулярно к плоскости основания.
, распределенной по ободу. Ось проходит через центр перпендикулярно к плоскости основания.
 Рассмотрим момент инерции обруча. Все малые элементы
Рассмотрим момент инерции обруча. Все малые элементы 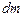 обруча находятся на одном и том же расстоянии
обруча находятся на одном и том же расстоянии 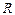 от его оси, проходящей через его центр масс С, поэтому
от его оси, проходящей через его центр масс С, поэтому 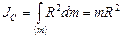 . (1.4.12)
. (1.4.12)
3) круглый однородный диск (цилиндр) радиусом 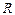 и массой
и массой  ; ось проходит через центр диска перпендикулярно к плоскости основания.
; ось проходит через центр диска перпендикулярно к плоскости основания.
|
 . По формуле 1.4.8.
. По формуле 1.4.8.  , где
, где 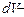 объем бесконечно тонкого кольца радиусом
объем бесконечно тонкого кольца радиусом  , толщиной
, толщиной и высотой
и высотой  . Т.к.
. Т.к.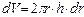 , то
, то
 . Подставим
. Подставим
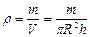 и получим
и получим  . (1.4.13)
. (1.4.13)
|
 Пусть
Пусть  внешний и внутренний радиусы цилиндра. Задача рассматривается аналогично предыдущему случаю, но т.к. цилиндр не сплошной, а полый внутри, то пределы интегрирования будут другими.
внешний и внутренний радиусы цилиндра. Задача рассматривается аналогично предыдущему случаю, но т.к. цилиндр не сплошной, а полый внутри, то пределы интегрирования будут другими.
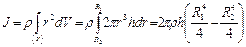 . Масса такого цилиндра
. Масса такого цилиндра 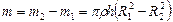 , откуда
, откуда . (1.4.14)
. (1.4.14)
 5) однородный шар радиусом
5) однородный шар радиусом 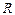 и массой
и массой 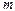 ; ось проходит через центр шара.
; ось проходит через центр шара.
|
 и имеющие радиусы
и имеющие радиусы 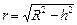 и массу
и массу 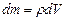 , где
, где  . Тогда по формуле (1.4.13)
. Тогда по формуле (1.4.13)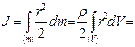


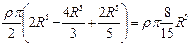 .Т.к.
.Т.к. ,то
,то 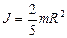 . (1.4.15)
. (1.4.15)
6) полый шар массой 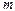 ; ось проходит через центр шара.
; ось проходит через центр шара.
Пусть 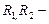 внешний и внутренний радиусы шара.
внешний и внутренний радиусы шара.  , где
, где  моменты инерции шаров с радиусами
моменты инерции шаров с радиусами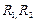 . Аналогично предыдущему случаю получаем
. Аналогично предыдущему случаю получаем 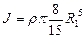

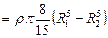 .
.
Т.к.  , то
, то 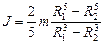 . (1.4.15)
. (1.4.15)
Пример 1.4.1. Два шара радиусами 2 см и массой 10 г каждый скреплены тонким невесомым стержнем длиной 20 см. Определить момент инерции системы относительно оси, перпендикулярной стержню и проходящей через центр тяжести.


|
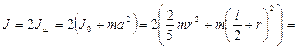

|
|
|
Ответ: 
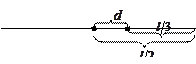 Пример 1.4.2. Определить момент инерции тонкого стержня длиной 30 см и массой 200 г относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на одну треть его длины.
Пример 1.4.2. Определить момент инерции тонкого стержня длиной 30 см и массой 200 г относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на одну треть его длины.
Найти положение центра масс системы.
|
 Решение:
Решение:
|
 По теореме Штейнера
По теореме Штейнера  .
.
По формуле, полученной в примере 1
для центра тяжести однородного стержня, находим 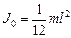 . Рас-
. Рас-
стояние  от центра тяжести стержня до заданной оси можно найти по рис.1.4.11, тогда
от центра тяжести стержня до заданной оси можно найти по рис.1.4.11, тогда  , и
, и 
Ответ:  .
.
Пример 1.4.3. Длина одной стороны плоской прямоугольной однородной пластины 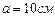 , масса
, масса  . Найти момент инерции
. Найти момент инерции 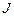 пластины относительно оси, совпадающей со второй ее стороной.
пластины относительно оси, совпадающей со второй ее стороной.


|
 По формуле 1.4.7.
По формуле 1.4.7.  . Т.к. данное тело однородно, т.е. его плотность
. Т.к. данное тело однородно, т.е. его плотность 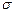 одинакова по всей плоскости, то
одинакова по всей плоскости, то 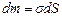 .
.

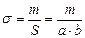 ,
,  и
и  . Получаем
. Получаем  .
.
Ответ: 
Пример 1.4.5. Диаметр диска  , масса
, масса  . На расстоянии 10 см от центра диска в плоскости диска находится центр отверстия диаметром
. На расстоянии 10 см от центра диска в плоскости диска находится центр отверстия диаметром  . Найти момент инерции
. Найти момент инерции  полученной фигуры относительно оси, проходящей через центр диска перпендикулярно к его плоскости.
полученной фигуры относительно оси, проходящей через центр диска перпендикулярно к его плоскости.
|
|
 Решение:
Решение:

 (1), где
(1), где  момент инерции сплошного диска;
момент инерции сплошного диска;  момент инерции вырезанной части. По теореме Штейнера
момент инерции вырезанной части. По теореме Штейнера 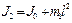 , где
, где  момент инерции вырезанной части относительно оси, проходящей через точку О,
момент инерции вырезанной части относительно оси, проходящей через точку О,  масса вырезанной части диска,
масса вырезанной части диска,
 (2),но
(2),но  , где
, где  площадь диска,
площадь диска, 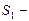 площадь вырезанной части диска,
площадь вырезанной части диска, 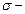 поверхностная площадь. Подставив
поверхностная площадь. Подставив  в уравнение (2), найдем
в уравнение (2), найдем  . Подставив в формулу (1) выражения
. Подставив в формулу (1) выражения 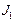
и  получим
получим 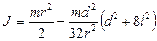 .
.
Ответ: 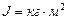
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 3510; Нарушение авторских прав?; Мы поможем в написании вашей работы!
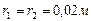 ,
,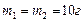 ,
, 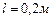

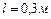 ,
,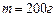 ,
, 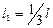
 ,
,
 ,
, ,
, 