Итерационные алгоритмы компоновки

Алгоритмы этой группы предназначены для улучшения некоторой начальной компоновки, полученной вручную или после последовательной компоновки.

Рассмотрим идею:

Пусть лучшему варианту компоновки соответствует минимум некоторого показателя P. При этом множество элементов схемы E разбито на 2 подмножества A и B. Обозначим исходный вариант компоновки 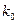, а начальное значение целевой функции 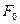(в результате компоновки её необходимо оптимизировать). Тогда предположим, что выбранная пара элементов 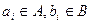и перестановка приводит к уменьшению значения целевой функции.

При перестановке элементов 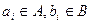местами, получим вариант компоновки 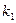и значение целевой функции 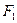. Причём приращение 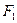будет равно:

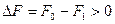
Процесс повторяется до тех пор пока существуют перестановки уменьшающие значение показателя P. В результате получаем последовательность вариантов компоновки 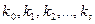, а также монотонно убывающее значение целевой функции.

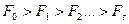
Расширить пространство поиска позволяет метод групповых перестановок (группового обмена).

Для всех пар элементов 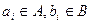определяется приращение значения .

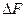При этом выбирается такая пара 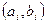, при котором приращение 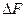максимальное (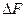может быть положительным или отрицательным или равным нулю). Процесс повторяют до тех пор пока уменьшается .

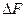Пример группового обмена уменьшения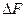

(множество суммарного веса рёбер)

Основные функции алгоритма:

1. Постановка задачи

Пусть множество вершин гиперграфа Х разбито на 2 непересекающихся подмножества 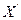и Х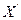

На основании формулы для расчёта внешних проводов

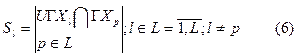
При перестановке 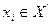и происходит изменение числа внешних связей, которое находится следующим образом.

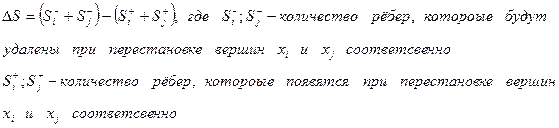
1. Основные пункты алгоритма

Для пары вершин 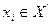и , определяются инцендентные им рёбра.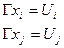

Находим множество вершин, входящих в каждое ребро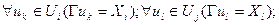

Подсчитываем показатель S, который показывает количество рёбер 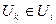, для которых выполняется следующее условие:

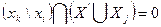
А также, здесь же рассчитываем 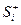- количество рёбер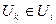

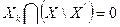
Подсчитываем 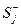- количество рёбер 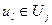, для которых справедливо условие:

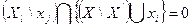
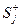-количество рёбер 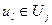, для которых справедливо следующее условие:

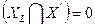
Определяем изменение числа внешних связей

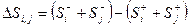
Повторяем пункт с 1 по 5 для всех возможных парных обменов

Находим максимальное значение 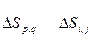и проверяем условие:

, если правда идём на пункт 2.8., иначе на пункт 2.12.

Осуществляем перестановку вершин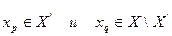

Для этих вершин определяем инцендентные им рёбра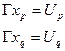

Находим множества вершин входящих в эти рёбра

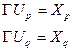
Повторяем пункт с 1 по 5 для всех возможных парных обменов, в которых участвуют вершины:

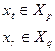
Идём на пункт 7

Конец работы алгоритма

Дата добавления: 2014-01-20