Гистограмма. Эмпирическое распределение результатов наблюдений

Чтобы получить представление о законе распределения измеряемой величины, экспериментальные данные группируют. Для этого весь интервал значений вели­чины от x _min до x _max (рис. 4.4) разбивают на несколько равных отрезков, называемых интервалами группировки данных, шириной Δ и центрами x_k, так что k -й интервал (k = 1, 2, …, K) имеет границы (x_k – Δ / 2, x_k + Δ / 2). Далее распределяют значения x_i по интервалам. Число точек N_k, оказавшихся внутри k -го интервала, даёт число попаданий измеряемой величины в этот интервал. Общее число точек, оказавшихся внутри всех интервалов разбиения, долж­но быть равно полному числу N результатов наблюдений в исходной выборке.

Над каждым интервалом Δ_k строится прямоугольник высотой f_k = N_k / (N Δ). Совокупность таких прямоугольников называется гистограммой (рис. 4.4).

При построении гистограмм интервалы разбиения не следует брать очень большими или очень маленькими. Так, в первом случае прямоугольники на гистограмме будут иметь примерно одинаковую высоту, а во втором – могут появиться интервалы, в которые не попадет ни одного значения случайной величины. Чтобы этого не происходило, придерживаются следующих правил:

• Число интервалов группировки данных К рассчитывают по формуле К = 1 + 3.2 lg N, где N – объем выборки.
• Если число К получается дробным, то eго округляют до ближайшего меньшего целого. Ширину интервалов берут равной Δ = (x _max – x _min)/ K.

Высоты и площади прямоугольников на гистограмме имеют следующий смысл. Поскольку относительные частоты P_k = N_k / N приближенно равны вероятности попадания результата каждого отдельного наблюдения в данный интервал, то высота каждого прямоугольника на гистограмме

f_k = N_k / N Δ = Р_k /Δ

есть вероятность, приходящаяся на единицу длины интервала разбиения или плотность вероятности попадания случайной величины в интервал Δ _k с центром в точке x_k.

Площадь каждого прямоугольника f_k Δ = N_k / N = Р_k есть вероятность попадания результата в интервал Δ _k. Сумма площадей прямоугольников, основания которых находятся внутри некоторого интервала [ x ₁, x ₂], равна вероятности для каждого отдельного наугад взятого результата попасть в этот интервал.

Нетрудно убедиться, что сумма площадей всех прямоугольников равна единице:

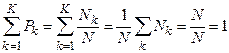. (4.1)

Это означает, что попадание произвольного результата наблюдения в какой-либо из интервалов разбиения в промежутке ( x _max, x _min) есть достоверное событие.

Из рис. 4.4 видно, что результаты наблюдений распределены около некоторого значения, абсцисса которого соответствует цен­тру самого высокого прямоугольника на гистограмме. По обе стороны данного прямоугольника расположены прямоугольники убывающих высот и площа­дей. Учитывая, что высоты прямоугольников f_k имеют смысл плотности вероятности попадания измеряемой величины в интервал Δ _k, можно сказать, что гистограмма дает представление о законе распределения измеряемой величины.

Зная координаты центров интервалов разбиения x_k и количества попаданий N_k значений измеряемой величины в интервалы, можно найти среднее значение измеряемой величины и величину , характеризующую разброс результатов наблюдений около среднего значения:

(4.2)

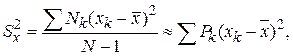(4.3)

где при большом объеме выборки . Величину называют эмпирической дисперсией, а 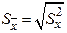– среднеквадратическим отклонением результатов наблюдений от среднего (СКО x) этот параметр характеризует ширину распределения значений случайной величины около среднего значения.

Если число наблюдений взять очень большим (), т. е. от выборки перейти к генеральной совокупности, а ширины интервалов разбиения очень маленькими, то ломаная огибающая гистограммы перейдет в плавную кривую, называемую функцией плотности распределения вероятности измеряемой величины, которую будем обозначать f (x). В этом случае суммы (4.1)–(4.3) заменятся интегралами, а вероятности P_k – вероятностями попадания случайной величины в интервал (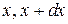). Если случайная величина распределена в интервале (a, b) (заметим, что границы интервала могут быть и бесконечными: ), то выражения (4.1)–(2.4) будут иметь вид

(4.4)

(4.5)

, (4.6)

где есть плотность вероятности распределения случайной величины или просто плотность вероятности; , – генеральные среднее и дисперсия.

Равенство (4.4) называют условием нормировки функции плотности вероятности. Это условие требует, чтобы площадь под графиком функции вероятности всегда была равна единице.

Закон распределения непрерывной случайной величины - соби­рательный термин, используемый для обозначения способов матема­тического описания непрерывной случайной величины. Закон рас­пределения может быть задан функцией распределения F(х) как уни­версальной характеристикой описания любых случайных величин и (или) плотностью распределения w(x), которая существует только для непрерывных случайных величин. Функции F(х) и w(x) несут о непрерывной случайной величине одну и ту же информацию, но в разной форме. Для их определе­ния необходимо проведение весьма длительных и кропотливых исследований и вычислений.

В большинстве случаев бывает дос­таточно охарактеризовать случайные величины с помощью ограниченного числа специальных параметров, основными из ко­торых являются:

• центр распределения;

• начальные и центральные моменты и производные от них ко­эффициенты – математическое ожидание (МО), Среднее квадратическое отклонение(СКО), эксцесс, контрэксцесс и коэффициент асимметрии.

Дата добавления: 2014-01-20