С двумя переменными

Задачи линейного программирования

Лекция 5

Линейного программирования

Графическое решение задач

Графический способ решения задач линейного программирования целесообразно использовать:

1) для решения задач с двумя переменными, в которых ограничения выражены неравенствами;

2) для решения задач со многими переменными при условии, что в их канонической записи содержится не более двух свободных переменных.

Целевая функция:

(5.1)

Ограничения:

(5.2)

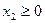, (5.3)

Каждое из неравенств (5.2) И (5.3) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми:

, , ,

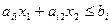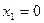В том случае, если система неравенств (5.2) и (5.3) совместна, то область ее решений есть множество точек, принадлежащих обеим ее полуплоскостям. Так как множество пересечений данных полуплоскостей выпуклое, то область допустимых значений тоже будет выпуклой. Такая фигура называется многоугольник. Его стороны лежат на прямых, уравнения которых получаются из исходной системы ограничений при замене знаков неравенства на знак «=».

Областью допустимых решений системы неравенств (5.2), (5.3) может быть:

­­–– выпуклый многоугольник;

–– выпуклая многоугольная неограниченная область;

–– пустая область;

–– луч;

–– отрезок;

–– единственная точка.

Целевая функция (5.1) определяет на плоскости совокупность прямых параллельных друг другу, каждой из которых соответствует определенное значение Z.

Вектор с координатами перпендикулярен этим прямым и указывает направление наискорейшего возрастания Z. Вектор, противоположный 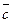, указывает наискорейшее убывание Z.

Если в одной и той же системе координат определить область допустимых решений системы неравенств (5.2) и (5.3) и семейство параллельных прямых (5.1), то задача определения максимума функции Z сведется к нахождению допустимой области точки, через которую проходит одна из прямых Z и которая соответствует наибольшему параметру Z.

Если такая точка существует, то многоугольник не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника целевая функция принимает максимальное значение. Для определения данной вершины построим линию уровня:

,

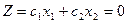проходящую через начало координат перпендикулярно вектору 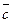. И будем передвигать ее в направление 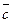до тех пор, пока она не коснется последней крайней точки многоугольника решений. Коэффициенты указанной точки определят оптимальный план данной задачи.

Заканчивая рассмотрение геометрической интерпретации задачи (5.2) и (5.3), при нахождении ее решения могут встречаться случаи А, Б, В, Г.

Рис. А характеризует такой случай, когда целевая функция принимает свое оптимальное решение в одной точке.

Рис. А

Из рис. Б видно, что максимальное значение функция Z принимает в любой точке отрезка АВ.

Рис. Б

На рис. В изображен случай, когда максимальное значение целевой функции недостижимо.

Рис. В

На рис. Г изображен случай, когда система ограничений задачи несовместна.

Рис. Г

Следует отметить, что нахождение минимального значения Z при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях. Отличие состоит в том, что при поиске максимального решения прямая Z двигается по вектору 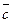, при поиске минимального значения – в обратном направлении.

Таким образом, отмеченные выше случаи встречаются при нахождении максимального значения функции. Они могут быть использованы и для нахождения минимального значения функции, но с обратным направлением .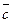

Для практического решения задач линейного программирования (5.2), (5.3) на основе геометрической интерпретации необходимо следующее:

1) построить прямые, уравнения которых получаются в результате замены в ограничениях (5.2) и (5.3) знаков неравенств на знаки равенств;

2) найти полуплоскости, определенные каждым из ограничений;

3) определить многоугольник решений;

4) построить вектор ;

5) построить прямую 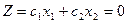, проходящую через начало координат и перпендикулярную ;

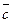6) передвигать прямую Z в направлении 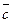, в результате чего определить точку или точки максимума функции Z или отсутствует ограничение функции Z сверху

7) определить точные координаты максимума функции и вычислить значение целевой функции в этой точке.

Пример: решение задач об ассортиментегеометрическим способом

Рис. 5.1

Построим многоугольник решений, для чего на плоскости x₁0x₂ проведем граничные прямые L₁, L₂, L₃, L₄.

L₁

L₂

L₃

L₄

Взяв начало координат за точку, которая удовлетворяет соответствующему неравенству, полуплоскости, определенные неравенством, показанные стрелками, область решений будет ABCD0.

Для построения прямой строим градиент и через 0 проводим прямую параллельную ему. Построенную прямую перемещаем параллельно самой себе в направлении .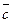

Из рис. 5.1 видно: по отношению к многоугольнику решений эта прямая остановится в точке c, где функция принимает максимальное значение.

Точка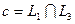

Для определения ее координат надо решить систему уравнений:

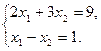
Из этого следует, что оптимальный план задачи:

x₁=2,4

x₂=1,4.

Подставляя x₁ и x₂ в линейную функцию, получим:

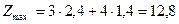
Полученное решение означает, что объем производства продукции П1 должен быть равным 2,4 денежных единицы, а объем продукции П2 –– 1,4 денежных единицы, при этом максимальная прибыль равна 12,8 денежных единицы.

Дата добавления: 2014-01-20