Релаксация импульса и энергии. Динамика установления равновесной функции распределения. Выравнивание электронной и ионной температур. Проводимость плазмы. Убегание электронов

Лекция 3.

Полученное в предыдущей лекции выражение для транспортного сечения позволяет найти скорость, с которой идет обмен импульсом и энергией между частицами плазмы.

Рассмотрим простейшую задачу: пучок быстрых электронов влетает в холодную плазму. Учтем сначала только столкновения электронов пучка с ионами плазмы. Из-за большой массы и малой тепловой скорости ионы можно считать бесконечно тяжелыми и покоящимися. В результате мы приходим к постановке задачи, в точности совпадающей с той, что рассматривали во второй лекции.

Пусть n обозначает плотность ионов. Со стороны пучка на ионы, находящиеся в единичном объеме, действует сила (см. 2.26)

По третьему закону Ньютона, точно такая же сила действует на единицу падающего пучка в противоположном направлении. Разделив ее на площадь пучка n_b, найдем силу F, действующую на одну частицу пучка;

. (3.1) Под действием этой силы пучок будет тормозиться, т.е. его направленная скорость u будет уменьшаться:

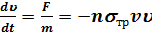. (3.2) Пользуясь этой формулой, нужно ясно понимать, что уменьшение направленной скорости пучка не связано с потерей энергии электронами, поскольку их рассеяние происходит на неподвижных тяжелых ионах. Средняя скорость пучка изменяется вследствие того, что электроны в результате столкновений начинают двигаться под углом к исходному направлению движения пучка. Нетрудно оценить, как растет со временем средний квадрат угла рассеяния q. Поскольку при рассеянии на малый угол q продольная скорость электрона изменяется на величину Dv = v(cosq - 1) @ -v q²/2, то уменьшение продольной скорости, описываемое уравнением (3.2), соответствует нарастание среднего квадрата угла:

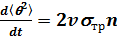(3.3) (усреднение, обозначенное угловыми скобками, производится по всем электронам пучка). Выражение (5.3) справедливо до тех пор, пока среднеквадратичный угол рассеяния мал по сравнению с единицей, т.е.

Из уравнений (3.2) и (3.3) видно, что характерное время t торможения и углового рассеяния по порядку величины равно ; величину, обратную t, называют частотой столкновений (электронов с ионами в рассматриваемом случае) и обозначают через n:

n_ei = ns_трv. (3.4) Пользуясь выражением, полученным в предыдущей лекции

, (2.34) получим практическую формулу для частоты электрон-ионных столкновений

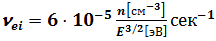. (3.5) Произведение vt, которое имеет смысл пути, проходимого электроном в направлении пучка за время торможения, называется длиной свободного пробега и обозначается через l:

. (3.6)

Естественно, что такие понятия, как длина пробега, частота столкновений и транспортное сечение, можно ввести не только для частиц пучка, но и для частиц плазмы. Нужно только представить, что на рассеивающий центр налетают частицы с разными скоростями и усреднить по распределению скоростей. Например, для максвелловского распределения скоростей значение Е² равно 15 Т ²/4. Поэтому числовые коэффициенты в практических формулах для усредненных значений s_тр, n _ei и l отличаются в 2-3 раза от формул (2.34), (3.5) и (3.6):

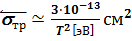, (2.34.1)

. (3.5.1)

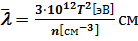. (3.6.1)

Рассмотрим теперь столкновения электронов пучка с электронами плазмы. Для этого нам придется обобщить задачу о столкновении двух заряженных частиц на случай, когда частицы имеют произвольные массы. Будем считать, что поток частиц с зарядом q₁e и массой m₁ налетает на покоящуюся (в начальный момент) частицу с зарядом q₂e и массой m₂. Чтобы описать рассеяние частиц сорта 1, надо решить уравнение движения

, (3.7) где r₁ и r₂ обозначают радиус-вектор частицы 1 и 2 соответственно. Для этого перейдем в систему центра масс, задаваемую радиус-вектором 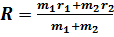, и введем разность r = r₁ – r₂, так что (см. рис. 3.1).

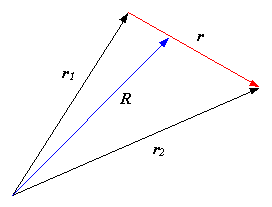
Рис. 3.1. Радиус-вектор R и разность

r = r₁ – r₂ для сталкивающихся частиц

Учитывая, что центр масс движется с постоянной скоростью, , получим

, (3.8) где m₁₂ =m₁m₂ /(m₁ + m₂) – приведенная масса. Мы будем называть частицу массы m₁₂ приведенной частицей. Ее положение задается вектором r. Согласно уравнению (3.8) движение частицы 1 можно найти, решив задачу о движении приведенной частицы, причем сила, действующая на реальную частицу 1, совпадает с силой, действующей на приведенную частицу. Если воспользоваться тем, что скорость этой частицы на бесконечности есть v, то мы получим, что сила, действующая на приведенные частицы (а, следовательно, и на частицу 1), равна

. (3.9) По сравнению с рассеянием на бесконечно тяжелых центрах отличие в силе проявляется только в том, что массу падающих частиц надо заменить m₁₂. Для электрон-электронных столкновений m₁₂ = m_e /2, и по порядку величины сила, действующая на пучок электронов со стороны электронов плазмы, равна силе, действующей со стороны ионов.

Принципиальное отличие электрон-электронных столкновений от рассеяния на»бесконечно» тяжелых ионах состоит в том, что теперь происходит передача энергии от электронов пучка к электронам плазмы.

Чтобы подсчитать скорость передачи энергии, заметим, что приведенная частица рассеивается на неподвижном центре и поэтому энергию не теряет. Ее скорость после рассеяния по абсолютной величине равна начальной скорости v. Рассмотрим процесс столкновения реальных частиц сначала в системе центра масс. Она движется со скоростью относительно лабораторной. Поскольку в этой системе скорость частицы 1 связана со скоростью приведенной частицы соотношением

,

то величина скорости частицы 1 после столкновения не меняется, а значит, обмена энергии между сталкивающимися частицами в этом системе не происходит. Переходя в лабораторную систему, мы должны заключить, что найденная выше сила F в единицу времени совершает работу, равную

,

Забирая энергию от пучка 1 и передавая ее плазменным электронам 2. Скорость изменения энергии частиц пучка в W = - Fv_ц.м. находим, используя найденную выше формулу для силы F:

. (3.10) Переписав это выражение в виде

, его можно интерпретировать так, что при m₁ << m₂ в каждом столкновении (частота которых равна nvs) передается доля энергии порядка m₁ / m₂. Таким образом, при электрон-электронных столкновениях передается значительная часть энергии налетающей частицы, а при электрон-ионных столкновениях – лишь ее малая доля.

Выше мы получили формулы для F и W в случае, когда пучок движется сквозь холодную плазму. Возникает вопрос, как они изменятся, если температура плазмы не равна нулю? Очевидно, что если температура плазмы настолько мала, что тепловая скорость частиц плазмы v_T много меньше скорости частиц пучка, то выражение для F и W практически не изменится. Если же 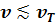, надо провести усреднение по скоростям частиц плазмы. Мы ограничимся нахождением силы F только в предельном случае .

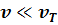Выберем группу частиц в плазме, скорость которых равна u^¢. Число таких частиц dn равно

dn = f (u^¢) d³v^¢n,

где обозначает f (u^¢) функцию распределения частиц, а f (u^¢) d³v^¢ есть вероятность частице иметь скорость u^¢. Сила трения частицы пучка о выбранную группу частиц плазмы равна

.

Теперь надо просуммировать эту силу по всем скоростям u^¢, что сводится к вычислению интеграла

. (3.11) В случае, когда f (u) – изотропная функция распределения, интеграл легко вычислить, воспользовавшись следующей электростатической аналогией. Если интегрировать u и u^¢ как радиус-векторы в пространстве координат, то интеграл (3.11) будет равен электрическому полю, создаваемому сферически симметрическим распределением зарядов с плотностью f (u). Как известно, поле сферически симметрического распределения зарядов на расстоянии v от центра равно заряду внутри сферы радиуса v, деленному на v². Поэтому

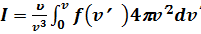. «Заряд», внешний по отношению к сфере , поле не создает. Так как мы предполагаем, что 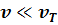, то последний интеграл приближенно равен f (0)´4 pv³ /3. Для максвелловской функции распределения

находим, что

. Следовательно, сила трения, усредненная по максвелловскому распределению, в пределах 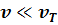равна

. (3.12)

В результате мы получили выражение для силы F трения в двух предельных случаях, 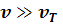и 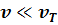. Подобным образом можно получить и выражение для W в пределах .

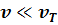Представим теперь, что в начальный момент электроны и ионы характеризуются неравновесными функциями распределения, отличными от максвелловских. Вследствие кулоновских столкновений функции распределения будут «максвеллизоваться».

Обозначим через W_e и W_i среднюю энергию, соответственно приходящую первоначально на один электрон и ион. Быстрее всего происходит релаксация распределения электронов вследствие электрон-электронных столкновений. За несколько таких столкновений электроны придут в термодинамическое равновесие с температурой T_e = 2 W_e /3 (полная энергия электронного газа при этом не изменится). Время установления равновесия в электронном газе t₁ примерно равно времени межэлектронных столкновений:

t₁ ~ t_ee. (3.13) Далее произойдет установление равновесия в ионном газе за время порядка ион-ионных столкновений,

, (3.14) при этом температура ионов станет равной T_i = 2 W_i /3. Самый медленный процесс – это выравнивание электронной и ионной температур. Оценим время выравнивания t₃, пользуясь формулой (3.10) для W и считая налетающими частицами электроны,

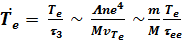, или 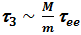. (3.15)

Применим развитые выше представления к задаче о протекании тока через плазму. Ток является откликом плазмы на внешнее электрическое поле Е. Под его действием, прежде всего, начинают ускоряться электроны, как самые легкие частицы. В результате возникают силы трения F со стороны ионов, которая в конечном итоге должна скомпенсировать электрическую силу,

eE + F = 0. (3.16)

Обозначим через u среднюю направленную скорость электронов, установившуюся в результате баланса между Е и F. Усреднив силу (3.12) по распределению электронов, нетрудно установить, что при 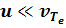сила трения пропорциональна u: F ~ mun_ei, причем частоту столкновений и сечение s_тр ~ Le⁴ / (T_e)² следует оценивать по тепловой скорости электронов. Полезно отметить, что скорость u относится только к средней направленной скорости движения электронов, тогда как случайная составляющая скорости равна . При усреднении по промежутку времени, за который происходит много столкновений, случайная составляющая силы обращается в нуль, и остается только часть, направленная против скорости u. Если же скорость направленного движения электронов превысит их тепловую скорость, 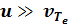, то частоту столкновений n_ei надо оценивать по скорости направленного движения u, тогда

.

Как видно из рис. 3.2, сила F, рассматриваемая как функция u, достигает максимального значения F_max, равного по порядку величины 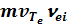, при .

Рис.3.2. Сила трения, как функция скорости u.

Если E > F_max / e = E_Dr, сила трения не может компенсировать электрическую силу ни при какой скорости электронов. В результате электроны будут безостановочно ускоряться. Этот эффект называют «убеганием» электронов. Минимальное электрическое поле, которое приводит к «убеганию», называется полем Драйсера:

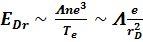. (3.17) Важно понимать, что поле Драйсера есть критическое поле для ухода в «просвист» основной группы электронов, имеющих скорость порядка тепловой. Однако даже при E < E_Dr в плазме имеются электроны (так называемые максвелловские хвосты), скорость которых значительно превышает тепловую скорость, 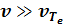. Сила трения, действующая на эти электроны мала, и они будут ускоряться даже в поле, меньше чем E_Dr.

Для малых полей, E << E_Dr, можно найти проводимость плазмы, выразив плотность тока j через электрическое поле E:

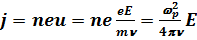, или отсюда следует, что

. (3.18)

Дата добавления: 2014-01-20