Лекция №3. Способы математического описания динамических систем

Способы математического описания динамических систем.

Для создания работоспособных систем управления и обеспечения оптимального качества их работы необходимо иметь математическое описание всех входящих в систему элементов.

Большинство систем АПК – это объекты управления сложной структуры, как в технологическом, так и в конструкторском плане.

В общем случае любые сложные системы можно описать в виде дифференциальных уравнений.

1. ДУ (нелинейные)

При описании системы в виде нелинейных ДУ значительно усложняется их интерпретация, решение, а также анализ и синтез систем.

2. Для таких сложных систем можно выделить стационарный и нестационарный режимы работы.

Стационарный режим работы – это установившийся режим, являющийся частным случаем совокупности общих режимов. Т.о. исследование подобных систем удобно описывать в виде ДУ.

В промышленности и АПК наиболее часто используются линейные и линеаризованные описания математических систем. Назовем их моделями.

Для описания динамики систем наиболее часто используются следующие модели:

§ ДУ (нелинейные);

§ Переходные характеристики;

§ Передаточные функции;

§ Частотные характеристики;

§ Вероятностные модели.

Для большинства объектов и систем ДУ отображают математическую связь между входными и выходными параметрами и производными от них.

Между входными и выходными величинами связь устанавливается на основании общих законов физики в виде линейных ДУ с постоянными коэффициентами.

При уточнении изменений между входами и выходами будут усложняться сами ДУ. Для упрощения моделей без потери концептуальной связи исходят из двух принципов ее представления:

1). Модель должна отражать важнейшие свойства объекта (явления) в поставленной задаче и описываться простыми зависимостями.

2). Выбор критериев приближения модели и действительного состояния должен быть связан с конечной целью решаемой задачи.

В общем случае линейное ДУ системы можно описать следующим образом:

n – мерное ДУ.

В данном уравнении постоянные коэффициенты Т имеют размерность времени.

И – коэффициент передачи системы.

Если система находится в равновесном состоянии, то все производные равны нулю. Имеем:

y(t)=K*x(t)

Если t = const, то y = K*x – уравнение статики.

Подобными уравнениями различной размерности можно описать любые явления и любые технологические процессы на промышленных системах.

Однако сами уравнения это всего лишь зависимости между входными и выходными параметрами, а решение этого уравнения при тех или иных воздействиях (входных) позволяет определить стратегию управления данным объектом (структурой).

Решение линейных ДУ динамических систем.

Проведем операции условного характера с рассмотренными ДУ:

1. Обозначим правую часть ДУ некоторой функцией f(x)

При таком подходе имеем линейное ДУ с неоднородной правой частью. Его решение определяется из двух составляющих:

y(t) = yпер(t) + yуст(t) – в общем виде.

Первый член yпер(t) – общее решение подбирается в каком-то заранее известном виде. Обычно его берут в виде суммы экспонент.

ci - определяется начальными значениями функции и ее производных.

рi – в форме характеристического уравнения.

Исходя из общего представления:

Характеристическое уравнение. Данное уравнение находится из исходного, используя преобразования Лапласа:

Предположим, что задана некоторая функция y(t) действительной переменной, для которой существует некоторое соотношение:

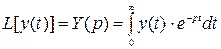
Это означает, что каждая функция y(t) поставлена в соответствии Y(p) комплексной переменной, где p=-a+iw.

В соответствии с этим определяют:

y(t) – оригинал функции

Y(t) – изображение.

Использование преобразования Лапласа позволяет перейти в математическое описание систем из области дифференциальных уравнений и описанию систем области алгебраических уравнений.

Решение алгебраического уравнения значительно проще и позволяет снизить объем заполненных операций.

Однако чтобы вернуться о временную область необходимо использовать обратное преобразование Лапласа, которое может быть неоднозначным. Поэтому выполнять обратное преобразование следует с учетом правой части ДУ.

Само преобразование Лапласа обладает рядом замечательных свойств. Например, дифференцированию оригинала y(t) соответствует операция умножения изображения на комплексную переменную р, а интегрированию оригинала y(t) соответствует операция деления Y(p) на р. Иначе говоря, в пространстве изображений мы переходим к алгебраическим операциям.

В операционном исчислении определены наиболее часто используемые изображения функций,

Составляющая решения при 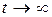может меняться 2 разными способами:

1. Если при 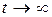, то среди корней характеристического уравнения имеются корни с положительной частью, это означает, что система неустойчива. Такие системы неработоспособны.

2. при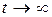

В структуре остается только установившаяся составляющая, которую называют переходным процессом.

Корни характеристического уравнения не имеют положительной действительной части. Система работоспособна.

При рассмотрении задач уравнения исследователя (проектировщика) интересна реакция (отклик) системы на вполне конкретные возмущения. Одним из таких воздействий является ступенчатое воздействие.

x(t)=0

x(t)=u(t)

1(t)=0, t<0

1(t)=1, t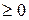

Однако производные ступенчатой функции при t=0 образуются в , что затрудняет решение ДУ, в которых справа стоят производные от x(t).

Поэтому было принято нормативное решение, что производная от ступенчатой функции представляется в операционном исчислении в виде некоторой функции:

В данной интерпретации это бесконечно короткий и бесконечно высокий импульс с единичной площадью.

Дата добавления: 2014-01-20