Теорема умова-пойнтинга для мгновенных значений

Кроме уравнений Максвелла, большое значение в теории электромагнитного поля имеет теорема Умова-Пойнтинга. Она описывает энергетические соотношения в поле.

Теорема Умова-Пойнтинга имеет две формы записи первая – для мгновенных значений, вторая – комплексная форма – для синусоидально изменяющихся величин.

Известно, что энергия электрического поля в единице объема равна 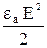. Энергия магнитного поля в единице объема – . Энергия в объеме равна

.

Для того чтобы образовать выражение, в которое вошла бы полная энергия в объеме , умножим (1) на , а (2) на . Получим:

; (9)

. (10)

Из (5) вычтем (6):

. (11)

Так как , то левая часть (11) есть – 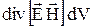. Следовательно,

.

Обозначим для сокращения записи векторное произведение 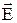на через , т.е. примем, что 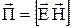; - это вектор, называемый вектором Пойнтинга; его единица измерения равна произведению размерностей Е и Н, т.е. .

Таким образом, вектор Пойнтинга имеет размерность мощности (или энергии в единицу времени), отнесенной к единице поверхности, и направление его (рисунок 1) совпадает с направлением движения острия правого винта, если головку последнего вращать по кратчайшему направлению от 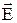на . Итак,

. (12)

Рисунок 1

Распространим (12) на некоторый объем конечных размеров. С этой целью проинтегрируем (12) по объему V:

. (13)

Подобно тому, как поверхностный интеграл по теореме Стокса преобразовывается в линейный (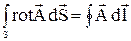), объемный интеграл в свою очередь может быть преобразован в поверхностный. Это преобразование осуществляют с помощью теоремы Остроградского-Гаусса:

.

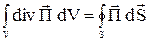Теорему Умова-Пойнтинга для мгновенных значений записывают следующим образом:

. (14)

Левая часть (14) представляет собой поток вектора Пойнтинга (направленный внутрь объема) сквозь любую замкнутую поверхность S, ограничивающую некоторый объем V.

В соответствии с уравнением Джоуля-Ленца в дифференциальной форме есть энергия, выделяющаяся в виде теплоты в единице объема в единицу времени.

Поэтому есть энергия, выделяющаяся в виде теплоты в единицу времени в объеме V; есть скорость изменения запаса электромагнитной энергии в единице объема.

Но скорость изменения электромагнитной энергии есть мощность.

Следовательно, поток вектора Пойнтинга сквозь любую замкнутую поверхность, ограничивающую объем V, равен мощности, выделяющейся в объеме V в виде теплоты, и мощности, идущей на приращение энергии электромагнитного поля.

Теорема Умова-Пойнтинга следует трактовать как уравнение энергетического баланса; левая часть (14) есть мощность или энергия в единицу времени, доставляемая в виде потока вектора Пойнтинга внутрь некоторого объема; правая часть (14) есть энергия, расходуемая в единицу времени внутри объема.

Соотношение (14) было получено в предположении, что среда внутри однородна и изотропна, а также в предположении, что отсутствует отраженная волна и внутри объема нет источников электродвижущей силы.

Если поле не изменяется во времени, то

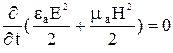и .

Электромагнитная энергия от места ее генерирования передается к месту потребления по диэлектрику (провода же в линиях передачи выполняют двоякую роль: они являются каналами, по которым проходит ток, и организаторами структуры поля в диэлектрике).

Покажем справедливость этого утверждения на простейшем примере. Пусть энергия постоянного тока передается по коаксиальному кабелю (рисунок 2). Радиус жилы 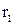, внутренний радиус оболочки 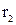. Примем проводимость материала жилы и оболочки настолько большой (теоретически бесконечно большой), что напряженности поля в жиле и оболочке стремятся к нулю. Пространство между жилой и оболочкой заполнено диэлектриком.

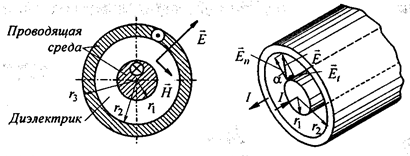
Рисунок 2

Убедимся, что энергия, передаваемая приемнику в единицу времени, равная , действительно канализируется по диэлектрику.

С этой целью подсчитаем поток вектора Пойнтинга через поперечное сечение диэлектрика, в рассматриваемом примере представляющее собой кольцо с внутренним радиусом 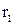и наружным 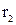. Напряженность магнитного поля в диэлектрике, по закону полного тока

.

Напряженность электрического поля в диэлектрике при постоянном токе определяется так же, как и в условиях электростатики:

,

где Q – полный заряд жилы на длине ;

U – напряжение между жилой и оболочкой.

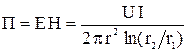
Следовательно, в некоторой точке диэлектрика, расположенной на расстоянии r от ос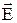и (),

(и взаимно перпендикулярны; рисунок 2). Поток вектора Пойнтинга через кольцо с радиусам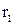и и :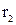

.

Таким образом, вся поступающая к приемнику энергия действительно передается по диэлектрику. По жиле и оболочке энергия к приемнику не передается. Более того, если учесть, что γ конечна и напряженность электрического поля в жиле и оболочке направлена по току и не равна нулю, то нетрудно убедиться в наличии потока вектора Пойнтинга через боковую поверхность провода внутрь провода, т.е. провода сами потребляют из диэлектрика энергию на покрытие тепловых потерь.

Дата добавления: 2014-01-20