
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция Дифракция
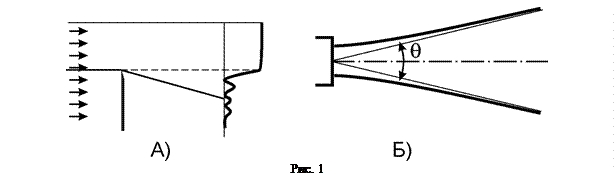
Принцип Гюйгенса. Интеграл Кирхгофа. Под дифракцией принято называть оптические эффекты, которые не могут быть объяснены с позиций геометрической оптики. В частности, под дифракцией подразумеваются явления, при которых свет отклоняется от прямолинейного распространения. Одним из примеров дифракции является проникновение света за границу тени от непрозрачной преграды (рис. 1А). Однако наличие преграды не является обязательным. Пример – лазерный пучок распространяется так, что его каустики представляют собой гиперболы (рис. 2Б).
Дифракцию можно объяснить с помощью принципа Гюйгенса – Френеля, который является следствием уравнений Максвелла. Такое объяснение не является единственным, но его достоинство заключается в наглядности, к тому же основные положения этого принципа были сформулированы еще до получения уравнений Максвелла.
 Суть принципа заключается в следующем. Каждая точка волнового фронта является точеным источником вторичной сферической волны, при этом его комплексная амплитуда
Суть принципа заключается в следующем. Каждая точка волнового фронта является точеным источником вторичной сферической волны, при этом его комплексная амплитуда 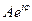 равна комплексной амплитуде исходной волны в данной точке. Комплексная амплитуда поля в произвольной точке пространства будет суммой комплексных амплитуд всех вторичных волн, т.е. их интерференции, в этой точке. Таким образом, принцип Гюйгенса позволяет определить распределение амплитуд и, соответственно, распределение освещенности во всех точках пространства, т.е. получить исчерпывающую характеристику электромагнитного поля.
равна комплексной амплитуде исходной волны в данной точке. Комплексная амплитуда поля в произвольной точке пространства будет суммой комплексных амплитуд всех вторичных волн, т.е. их интерференции, в этой точке. Таким образом, принцип Гюйгенса позволяет определить распределение амплитуд и, соответственно, распределение освещенности во всех точках пространства, т.е. получить исчерпывающую характеристику электромагнитного поля.
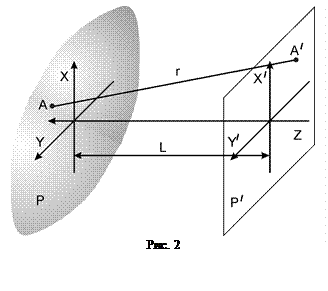
Получим математическую запись этого принципа. Зададим некоторую поверхность  , через которую проходит исходная волна. Определим связанную с ней систему координат
, через которую проходит исходная волна. Определим связанную с ней систему координат 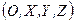 . Через произвольную точку пространства
. Через произвольную точку пространства 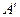 , в которой требуется определить амплитуду поля, проведем плоскость
, в которой требуется определить амплитуду поля, проведем плоскость 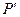 , параллельную координатной плоскости
, параллельную координатной плоскости 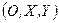 и определим в ней систему координат
и определим в ней систему координат 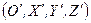 так, что ее оси были параллельны соответствующим осям
так, что ее оси были параллельны соответствующим осям 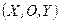 . Возьмем на
. Возьмем на  произвольную точку
произвольную точку 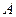 с координатами
с координатами 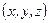 , при этом
, при этом  , где
, где 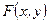 - уравнение поверхности
- уравнение поверхности  . Согласно вышеизложенному, в ней находится точечный источник с комплексной амплитудой
. Согласно вышеизложенному, в ней находится точечный источник с комплексной амплитудой
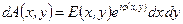 , ,
| (1) |
где 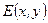 и
и 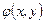 [1] - амплитуда и фаза падающей волны в этой точке. Уравнение сферической волны, вышедшей из
[1] - амплитуда и фаза падающей волны в этой точке. Уравнение сферической волны, вышедшей из 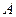 в точке
в точке 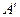 с координатами
с координатами 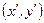 будет
будет
 , ,
| (2) |
где  радиус сферы, в данном случае равным расстоянию между точками
радиус сферы, в данном случае равным расстоянию между точками 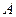 и
и 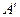 ,
, 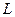 - расстояние между началами координат
- расстояние между началами координат 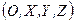 и
и 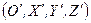 . Таким образом комплексная амплитуда волны в точке
. Таким образом комплексная амплитуда волны в точке 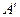 , вышедшей из точки
, вышедшей из точки 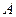 будет
будет
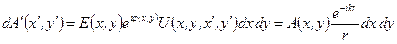 . .
| (3) |
Полная амплитуда в точке 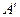 есть сумма амплитуд сферических волн от всех вторичных источников, т.е. интеграл
есть сумма амплитуд сферических волн от всех вторичных источников, т.е. интеграл
 , ,
| (4) |
где 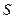 - область поверхности
- область поверхности  , в которой расположены вторичные источники.
, в которой расположены вторичные источники.
Полученное выражение представляет собой дифракционный интеграл в приближении Кирхгофа. Вычисление этого интеграла позволит решить поставленную задачу – по заданному значению поля на некоторой поверхности определить амплитуду электромагнитного поля в любой точке пространства.
Однако вычисление этого интеграла сопряжено с большими трудностями. Прежде всего, существует крайне мало функций 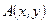 , для которых результат интегрирования выражается через конечное число функций, т.е. представим в аналитическом виде. Кроме того, использование вычислительных средств приводит к недопустимо большим затратам машинного времени. Это происходит из-за осциллирующего характера подынтегральной функции. Дело в том, что сомножитель
, для которых результат интегрирования выражается через конечное число функций, т.е. представим в аналитическом виде. Кроме того, использование вычислительных средств приводит к недопустимо большим затратам машинного времени. Это происходит из-за осциллирующего характера подынтегральной функции. Дело в том, что сомножитель 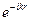 , который в силу формулы Эйлера выражается через синус и косинус, аргументы, которых содержат большое число (например, для
, который в силу формулы Эйлера выражается через синус и косинус, аргументы, которых содержат большое число (например, для 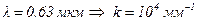 ). Такая функция будет менять знак через 0.63 мкм и при интегрировании (к примеру) по квадратной площадке 10
). Такая функция будет менять знак через 0.63 мкм и при интегрировании (к примеру) по квадратной площадке 10 10 мм число перемен знака у подынтегральной функции будет порядка
10 мм число перемен знака у подынтегральной функции будет порядка  . Для получения хотя бы примерного результата необходимо эту цифру умножить минимум в 6 раз, поскольку большинство алгоритмов интегрирования вычисляют площадь под кривой (в данном случае объем под поверхностью). Надо сказать, что существуют специальные алгоритмы вычисления таких интегралов, время выполнения которых существенно меньше, но все равно затраты времени недопустимо высоки.
. Для получения хотя бы примерного результата необходимо эту цифру умножить минимум в 6 раз, поскольку большинство алгоритмов интегрирования вычисляют площадь под кривой (в данном случае объем под поверхностью). Надо сказать, что существуют специальные алгоритмы вычисления таких интегралов, время выполнения которых существенно меньше, но все равно затраты времени недопустимо высоки.
Тем не менее, попытки вычисления таких интегралов предпринимались, и первая оценка его величины была осуществлена Френелем с помощью так называемого методом зон Френеля. Он достаточно хорошо изложен в курсе физики, поэтому напомним лишь его основную идею и выводы. Суть его заключается в следующем. Сферический волновой фронт, исходящий из точечного источника 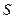 , на котором располагаются вторичные источники, разбивается на ряд концентричных оси зон так, чтобы разность хода от середин двух соседних зон равнялась половине длины волны (рис. 3).
, на котором располагаются вторичные источники, разбивается на ряд концентричных оси зон так, чтобы разность хода от середин двух соседних зон равнялась половине длины волны (рис. 3).

| (5) |
Доказывается, что площади этих зон почти равны, поэтому световые потоки от вторичных источников в этих зонах почти равны и так как в соседних зонах они в противофазе, в точке 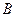 эти потоки взаимно уничтожаются. Таким образом, если рассматривать дифракцию на отверстии, то если на нем помещается четное число зон, то в точке
эти потоки взаимно уничтожаются. Таким образом, если рассматривать дифракцию на отверстии, то если на нем помещается четное число зон, то в точке 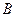 будет минимум освещенности, а если четное, то максимум. Радиус
будет минимум освещенности, а если четное, то максимум. Радиус  зоны
зоны 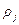 Френеля вычисляется по формуле
Френеля вычисляется по формуле
 , ,
| (6) |
где  - расстояние по оси от источника до отверстия;
- расстояние по оси от источника до отверстия; 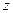 - расстояние от отверстия до точки наблюдения
- расстояние от отверстия до точки наблюдения  . Если источник в бесконечности, т.е. на отверстие освещается параллельным пучком, то выражение (6) упрощается
. Если источник в бесконечности, т.е. на отверстие освещается параллельным пучком, то выражение (6) упрощается
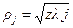 . .
| (7) |
 С помощью зон Френеля легко объясняется дифракционный эффект, называемый пятном Пуассона. Если на пути параллельного пучка лучей поместить препятствие так, что его размер будет равен первой зоне Френеля, то согласно вышеизложенному, в точке
С помощью зон Френеля легко объясняется дифракционный эффект, называемый пятном Пуассона. Если на пути параллельного пучка лучей поместить препятствие так, что его размер будет равен первой зоне Френеля, то согласно вышеизложенному, в точке 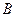 будет максимум освещенности, т.е. яркое пятно (рис. 4). Это противоречит геометрической оптике, поскольку точка
будет максимум освещенности, т.е. яркое пятно (рис. 4). Это противоречит геометрической оптике, поскольку точка 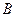 находится в центре тени от препятствия. Это эффект можно использовать для определения границы применения приближения геометрической оптики – если соотношение между размером препятствия
находится в центре тени от препятствия. Это эффект можно использовать для определения границы применения приближения геометрической оптики – если соотношение между размером препятствия  , расстояния от него
, расстояния от него 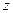 и длиной волны излучения таковы, что размер препятствия порядка первой зоны Френеля, т.е.
и длиной волны излучения таковы, что размер препятствия порядка первой зоны Френеля, т.е.
 , ,
| (8) |
то необходимо учитывать волновые свойства света - приближение геометрической оптики в данном случае неправомерно.
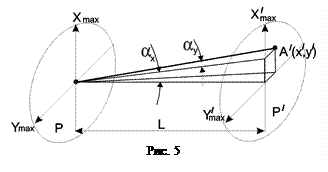 Дифракционные приближения. Дифракционные интегралы. Отмечалось, что дифракционный интеграл Кирхгофа неудобен для вычислений. Напомним, что физически этот интеграл представляет сумму вторичных сферических волн. Однако волновые свойства свет проявляет, в основном, в пучках с малой расходимостью, т.е. в узких пучках. В противном же случае аберрационные эффекты значительно сильнее волновых и вычисление дифракционных интегралов теряет смысл. Таким образом, на практике необходимо учитывать лишь небольшую часть сферических волновых фронтов вторичных волн. Это обстоятельство позволяет существенно упростить дифракционный интеграл и придать ему вид, значительно более удобный для практического использования. Таким образом, необходимо рассматривать такую геометрию распространения света, когда характерный размер объекта, на котором происходит дифракция
Дифракционные приближения. Дифракционные интегралы. Отмечалось, что дифракционный интеграл Кирхгофа неудобен для вычислений. Напомним, что физически этот интеграл представляет сумму вторичных сферических волн. Однако волновые свойства свет проявляет, в основном, в пучках с малой расходимостью, т.е. в узких пучках. В противном же случае аберрационные эффекты значительно сильнее волновых и вычисление дифракционных интегралов теряет смысл. Таким образом, на практике необходимо учитывать лишь небольшую часть сферических волновых фронтов вторичных волн. Это обстоятельство позволяет существенно упростить дифракционный интеграл и придать ему вид, значительно более удобный для практического использования. Таким образом, необходимо рассматривать такую геометрию распространения света, когда характерный размер объекта, на котором происходит дифракция 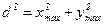 и размер области, где она наблюдается
и размер области, где она наблюдается 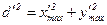 , значительно меньше расстояния между ними
, значительно меньше расстояния между ними 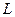 (рис. 5), т.е.
(рис. 5), т.е.
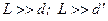 . .
| (9) |
Выберем в качестве поверхности вторичных источников плоскость (
( и используя соотношения (9), преобразуем выражение для
и используя соотношения (9), преобразуем выражение для 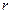 с помощью разложения
с помощью разложения 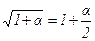 для
для 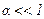
 . .
| (10) |
Тогда для экспоненты 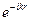
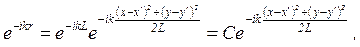
| (11а) |
где 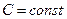 , но для
, но для 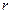 в знаменателе
в знаменателе
 , ,
| (11б) |
в силу соотношений (9).
Объединяя константы в (11а) и (11б) в одну, запишем интеграл в виде
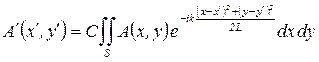 . .
| (12) |
Полученное выражение называется дифракционным интегралом в приближении Френеля, а условия, когда такое приближение справедливо, иногда называют волновой зоной. Геометрически это приближение означает замену сферы параболоидом вращения. Этот интеграл значительно проще. В частности, если 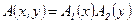 , то переменные в подынтегральном выражении разделяются и двукратный интеграл заменяется произведением двух однократных, что приводит к принципиальному упрощению.
, то переменные в подынтегральном выражении разделяются и двукратный интеграл заменяется произведением двух однократных, что приводит к принципиальному упрощению.
При дальнейшем уменьшении угла расходимости пучка, или что эквивалентно усилению соотношения (9), можно считать, что в формировании дифракционной картины участвует такая малая часть сфер вторичных волн, что эти волны можно считать плоскими. Математически это означает, что в показателе экспоненты подынтегрального выражения можно пренебречь квадратами переменных и интеграл (12) примет вид
 . .
| (13) |
Этот интеграл называется дифракционным интегралом в приближении Фраунгофера, а условия его выполнения называют дальней зоной. Необходимо отметить, что условия приближения Кирхгофа называются ближней зоной.
Интегралы (12) и (13) представляют собой так называемые интегральные преобразования, так как они ставят в соответствие функции 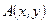 функцию
функцию 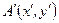 , при этом (12) является преобразованием Френеля, а (13) – преобразованием Фурье. Выражение (13) представляет собой сумму плоских наклонных волн с углами (рис.5)
, при этом (12) является преобразованием Френеля, а (13) – преобразованием Фурье. Выражение (13) представляет собой сумму плоских наклонных волн с углами (рис.5)
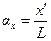 и и  . .
| (14) |
Если дифрагирующий объект поставить перед линзой с фокусным расстоянием 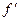 , то все лучи с углами наклона (14), т.е. параллельные между собой, соберутся в фокальной плоскости в точке с координатами в фокальной плоскости
, то все лучи с углами наклона (14), т.е. параллельные между собой, соберутся в фокальной плоскости в точке с координатами в фокальной плоскости 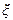 и
и 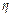 , определяемые соотношениями
, определяемые соотношениями
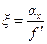 и и 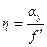 . .
| (15) |
Комбинируя (14) и (15) и подставляя результат в (13) интеграл можно записать как
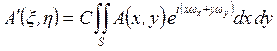 . .
| (15) |
 где
где  ,
, 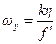 . Величины
. Величины 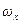 и
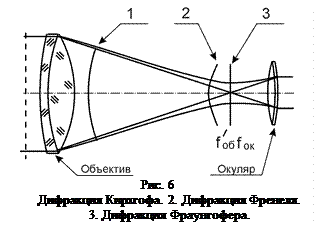
и 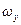 носят названия пространственных частот. При таких обозначениях выражение (15) формально совпадает с выражением для спектрального разложения электрических сигналов. Оказывается, что эта аналогия далеко не формальна и выражение (15) лежит в основе Фурье – оптики и оптической обработки информации. Таким образом, дифракцию Фраунгофера можно наблюдать в фокальной плоскости линзы (рис. 6). Заметим, что волновой фронт в фокальной плоскости плоский. Вблизи фокальной плоскости выполняются условия дифракции Френеля и вдали от нее – условия для дифракции Кирхгофа. Видно, что отклонения от геометрической оптики в случае дифракции Кирхгофа минимальны. Этот рисунок иллюстрирует неприемлемость приближения геометрической оптики вблизи фокальной плоскости – если луч определить как нормаль к волновому фронту, то вблизи линзы луч наклонен к оси, а в фокальной плоскости он ей параллелен. Таким образом, наблюдается отклонение от прямолинейного распространения.
носят названия пространственных частот. При таких обозначениях выражение (15) формально совпадает с выражением для спектрального разложения электрических сигналов. Оказывается, что эта аналогия далеко не формальна и выражение (15) лежит в основе Фурье – оптики и оптической обработки информации. Таким образом, дифракцию Фраунгофера можно наблюдать в фокальной плоскости линзы (рис. 6). Заметим, что волновой фронт в фокальной плоскости плоский. Вблизи фокальной плоскости выполняются условия дифракции Френеля и вдали от нее – условия для дифракции Кирхгофа. Видно, что отклонения от геометрической оптики в случае дифракции Кирхгофа минимальны. Этот рисунок иллюстрирует неприемлемость приближения геометрической оптики вблизи фокальной плоскости – если луч определить как нормаль к волновому фронту, то вблизи линзы луч наклонен к оси, а в фокальной плоскости он ей параллелен. Таким образом, наблюдается отклонение от прямолинейного распространения.
Так как размер дифракционной картины мал, то ее удобно наблюдать через окуляр. Такая двухкомпонентная система является зрительной трубой (рис.6).
|
Дата добавления: 2014-01-20; Просмотров: 1050; Нарушение авторских прав?; Мы поможем в написании вашей работы!