Признаки сходимости

Лицензирование в регулировании лизинговых отношений

Порядок заключения и исполнения договора лизинга.

Договор лизинга независимо от срока его действия заключается в письменном виде. В названии договора лизинга определяется его форма и вид.

К обязательным договорам относится договор купли-продажи.

К сопутствующим договорам относится договор о привлечении денежных средств, договор залога, договор гарантии, договор поручительства.

Договор лизинга должен содержать следующие существенные положения:

· точное описание предмета лизинга,

· объем передаваемых прав собственности;

· наименование места и указание порядка передачи предмета лизинга, срок действия договора лизинга;

· порядок учета предмета договора на балансе;

· порядок содержания и ремонта предмета лизинга;

· перечень дополнительных услуг, предоставляемых лизингодателем на основе договора;

· общая сумма договора лизинга;

В договоре лизинга в обязательном порядке должны быть оговорены обстоятельства, которые стороны считают бесспорным. К таким нарушениям обстоятельств можно отнести:

* использование предмета лизинга не по назначению;

* неподдержание предмета лизинга в исправном состоянии,;

* нарушение сроков (более 2 раз) сроков платежа за пользование предметом договора.

Гарантийное обслуживание предмета договора может осуществляться продавцом(поставщиком), если это предусмотрено договором купли- продажи.

Лизингополучатель за свой счет осуществляет техническое обслуживание лизинга, если это не предусмотрено договором лизинга.

Капитальный ремонт имущества, являющееся предметом лизинга, осуществляется лизингодателем, если иное не предусмотрено договором лизинга.

Лицензирование лизинговой деятельности осуществляется на основании положения о лицензировании финансовой аренды в РФ, утвержденного Постановлением Правительства РФ от 1 февраля 2001г. №80ю лицензия выдается на пятилетний срок, если в заявлении не указан меньший срок. Срок действия лостаточного капитала для приобретения оборудования в собственность.

Признак сравнения. Если функции f (x) и g (x) удовлетворяют на полуинтервале [ a, b) неравенству 0≤ f (x)≤ g (x) и интегрируемы на любом отрезке [ a, η ], a < η < b, то а) из сходимости интеграла 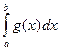следует сходимость интеграла 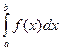; б) из расходимости интеграла 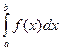вытекает расходимость интеграла .

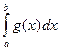Предельный признак сравнения. Если g (x)>0 на [ a, b), f и g интегрируемы на [ a, η ] для всех a < η < b и существует

= l,

причём l ¹0, l ¹¥, то интегралы 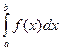и 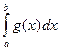сходятся или расходятся одновременно.

Если функция f (x) не знакопостоянна на промежутке [ a, b), то кроме сходимости несобственного интеграла рассматривают ещё и абсолютную сходимость интеграла.

Несобственный интеграл

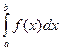
называется абсолютно сходящимся, если сходится интеграл

.

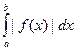Абсолютно сходящийся интеграл сходится. Обратное верно не всегда. Сходящийся несобственный интеграл, расходящийся абсолютно, называется условно сходящимся.

Для исследования на сходимость интегралов от незнакопостоянных функций часто применяются признаки Абеля и Дирихле.

Признак Абеля. Пусть функции f (x) и g (x) определены на промежутке [ a, b) и интегрируемы на любом отрезке [ a, η ] при a < η < b. Несобственный интеграл

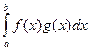
сходится, если выполняются условия

а) Интеграл 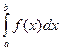сходится.

б) Функция g (x) монотонна на [ a, b) и ограничена, т.е. | g (x)|≤ M при x Î[ a, b), M - постоянная.

Признак Дирихле. Пусть функции f (x) и g (x) определены на [ a, b) и интегрируемы на [ a, η ] для всех η Î (a, b). Тогда несобственный интеграл

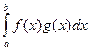
сходится, если выполняются условия:

а) функция F(η)= 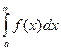ограничена на [ a, b), т.е.

| F(η)|=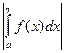≤ L, L - постоянная, η Î(a, b);

б) функция g (x) ограничена, монотонна на [ a, b) и

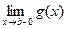=0.

Замечание. Аналогично рассматривается случай, когда особой точкой является x = a. Для этого случая все признаки переформулируются с очевидными изменениями.

18. Рассмотрим примеры.

Исследовать на сходимость интегралы (3.6.-3.10.).

3.6.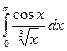. 3.7..

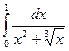3.8.. 3.9..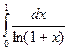

3.10..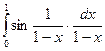

Решение.

3.6. Применим признак Абеля. Интеграл 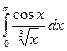сходится (см. задачу 3.1.), функция g (x)=cos x на [0, π ] монотонна и ограничена. По признаку Абеля интеграл сходится.

3.7. Так как f (x)=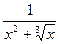=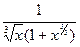≤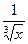= g (x), то по признаку сравнения интеграл сходится. Сходимость интеграла от g (x)=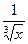(следует из задачи 3.1.).

3.8. Подынтегральная функция имеет особую точку в нуле, так как не определена там. Поэтому запишем интеграл в виде суммы

=+.

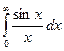Второй интеграл рассмотрен в задаче 2.19. Рассмотрим первый. Так как =1, то положив

f (x)=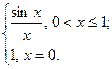

мы получаем непрерывную на [0,1] функцию. Так как непрерывная на отрезке функция интегрируема в обычном (собственном) смысле, то первый интеграл существует и, следовательно, наш интеграл сходится.

3.9. Применим предельный признак сравнения. Рассмотрим f (x)=и g (x)=.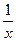

Вычисляем предел

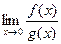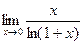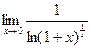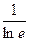====1.

Следовательно, наш интеграл может сходиться только вместе с интегралом 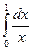. Но этот интеграл расходится, значит и наш интеграл расходится.

3.10. Применим признак Дирихле. Перепишем подынтегральную функцию в виде

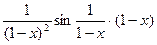
и положим f (x)= , g (x)=1- x.

Имеем

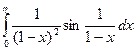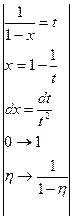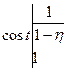====cos1-.

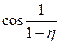Отсюда следует

≤2, 0< η <1,

и так как g (x)=1- x монотонна на [0,1] и =0, то по признаку Дирихле наш интеграл сходится.

19. Вычислить несобственные интегралы (3.11. - 3.15.)

3.11.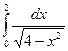. 3.12..

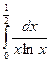3.13.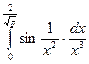. 3.14..

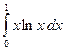3.15..

Исследовать на сходимость интегралы (3.16. - 3.20.)

3.16.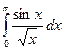. 3.17..

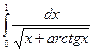3.18.. 3.19..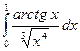

3.20..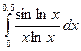

§4. Приближённые вычисления определённых интегралов.

20. Формула трапеций. Разобьём отрезок [ a, b ] на n равных частей точками x_k = a + kh, где 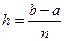, k =0,1,…, n. Для приближённого вычисления интеграла можно применить формулу трапеций:

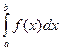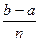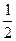»[ f (x₀)+ f (x₁)+…+ f (x_n-1)+ 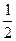f (x_n)].

Пусть функция f имеет на отрезке [ a, b ] ограниченную вторую производную f¢¢. Тогда погрешность R вычисления в формуле трапеций оценивается следующим образом:

| R |≤=,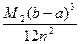

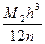где M ₂=.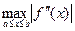

Формула Симпсона (формула парабол). Разобьём отрезок [ a, b ] на 2 n равных частей точками x_k = a + kh, где . Для приближённого вычисления используется формула Симпсона (формула трапеций):

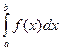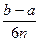»{ f (x₀)+ f (x_2n)+4[ f (x₁)+ f (x₃)…+ f (x_2n-1)]+ 2[ f (x₂)+ f (x₄)+…+ f (x_2n-2)]}.

Если функция f (x) имеет на отрезке [ a, b ] ограниченную четвёртую производную , то погрешность R формулы Симпсона можно оценить так:

| R |≤=,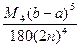

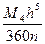где M ₄=.

21. Рассмотрим примеры (Примеры взяты из книги И.А. Марона «Дифференциальное и интегральное исчисление в примерах и задачах» М. «Наука», 1970).

4.1. Вычислить интеграл

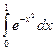
с точностью до 0,01 по формуле трапеций.

Решение. Вычислим вторую производную от f (x)=. Получим =(4 x ²-2). Несложно найти M ₂=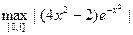=2. Таким образом, погрешность R формулы трапеций в данном случае оценивается так:

| R |≤=.

Чтобы достигнуть требуемой точности число n следует выбрать из неравенства <0,01. Решая неравенство, получаем n >4. Возьмём n =5. Тогда h =0,2. Составим таблицу (x_k =0,2 k, k =0,1,2,3,4,5). Вычисления будем вести с четырьмя знаками после запятой.

k	xk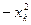
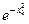
	0,2	-0,04	0,9608
	0,4	-0,16	0,8521
	0,6	-0,36	0,6977
	0,8	-0,64	0,5273
	1,0	-1,00	0,3679

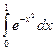»0,12[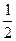+0,9608+0,8521+0,6977+0,5273+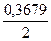]=0,2×3,72185=0,7444.

4.2. Вычислить по формуле Симпсона интеграл 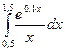с точностью до 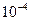=0,0001.

Решение. Чтобы добиться заданной точности надо определить число отрезков разбиения 2 n. Найдём четвёртую производную от f (x)=. Последовательно дифференцируя, находим

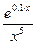=(0,0001× x ⁴-0,0004× x ³+0,12× x ²-2,4 x +24)=,

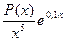где P (x) - многочлен, заключённый в круглых скобках. Мы не будем искать точное значение M ₄=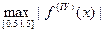, нам достаточно постоянной M такой, что M ₄≤ M. Поэтому мы оценим сумму модулей отдельных слагаемых, входящих в сумму 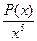. Имеем

≤++++.

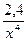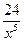Все слагаемые - убывающие на [0,5;1,5] функции, принимающие наибольшее значение при x =0,5. Следовательно,

≤0,0002+0,016+0,96+38,4+768<808, при x Î[0,5;1,5]. Учитывая, что e ^{0,1× x} - возрастающая функция, находим e ^{0,1× x} ≤ e^0,15 <1,2, x Î[0,5;1,5]. Таким образом,

≤808×1,2<1000

при x Î[0,5;1,5]. Число 2 n определится из неравенства

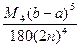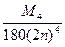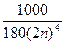=<<0,0001.

Решая неравенство относительно 2 n, получаем, 2 n >15. Возьмём 2 n =20. Тогда шаг h интегрирования будет равным

h =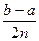==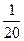0,05.

При более точном подсчёте получается, что при 2 n =20

| R |<3,5×10^-5.

Если мы будем подсчитывать y_i =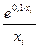с пятью знаками после запятой, т.е. с погрешностью не более 10^-5, то ошибка окончательного округления будет тоже не больше 10^-5. Таким образом, общая ошибка будет меньше, чем 4,5×10^-5<0,0001.

Составим таблицу значений функции y =для значений x от 0,5 до1,5 с шагом h =0,05. Вычисления ведутся с пятью знаками после запятой.

i	xi	0,1 xi	e ^0,1 xi	yi =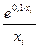
	0,50	0,050	1,05127	2,10254
	0,55	0,055	1,05654	1,92098
	0,60	0,060	1,06184	1,76973
	0,65	0,065	1,06716	1,64178
	0,70	0,070	1,07251	1,53216
	0,75	0,075	1,07788	1,43717
	0,80	0,080	1,08329	1,35411
	0,85	0,085	1,08872	1,28085
	0,90	0,090	1,09417	1,21574
	0,95	0,095	1,09966	1,15754
	1,00	0,100	1,10517	1,10517
	1,05	0,105	1,11071	1,05782
	1,10	0,110	1,11628	1,01480
	1,15	0,1,15	1,12187	0,97554
	1,20	0,120	1,12750	0,93958
	1,25	0,125	1,13315	0,90652
	1,30	0,130	1,13883	0,87602
	1,35	0,135	1,14454	0,84781
	1,40	0,140	1,15027	0,82162
	1,45	0,145	1,15604	0,79727
	1,50	0,150	1,16183	0,77455

Сведём полученные данные в следующую таблицу

i	xi	yi =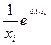
при i =0 и i =20	при нечётном i	при чётном i
	0,50	2,10254
	0,55		1,92098
	0,60			1,76973
	0,65		1,64178
	0,70			1,53216
	0,75		1,43717
	0,80			1,35411
	0,85		1,28085
	0,90			1,21574
	0,95		1,15754
	1,00			1,10517
	1,05		1,05782
	1,10			1,01480
	1,15		0,97554
	1,20			0,93958
	1,25		0,90652
	1,30			0,87602
	1,35		0,84781
	1,40			0,82162
	1,35		0,79727
	1,50	0,77455
	å=2,87709	å=12,02328	å=10,62893

Применяя формулу Симпсона, получаем

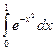»(2,87709+4×12,02328+2×10,62893)= ×72,22807=1,2038.

4.3. С помощью формулы трапеций вычислить

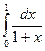
при n =8 и оценить допустимую погрешность.

4.4. Вычислить интеграл

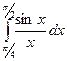
с точностью до 0,001 по формуле Симпсона. Считать, что M ₄=<177.

§.5. Геометрические приложения определённого интеграла.

Дата добавления: 2014-01-20