
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление площадей плоских фигур. Основные формулы
|
|
|
|
Если фигура на плоскости x O y ограничена прямыми x = a, y = b (a < b) и графиками функций y = j (x), y = y (x), причём, j (x)≤ y (x) (a ≤ x ≤ b), то её площадь вычисляется по формуле
S=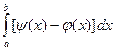 .
.
В полярных координатах площадь сектора, ограниченного дугой кривой r = r (j) и лучами j = a и j = b (a ≤ b), вычисляется по формуле
S=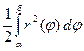 .
.
Если граница фигуры задана параметрическими уравнениями
x =(t), y =(t), то площадь фигуры вычисляется по одной из формул:
S =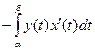 , S =
, S =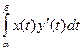 , S =
, S =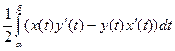 где a и b - значения параметра t, соответствующие началу и концу обхода контура в положительном направлении, при котором фигура остаётся слева.
где a и b - значения параметра t, соответствующие началу и концу обхода контура в положительном направлении, при котором фигура остаётся слева.
23. Рассмотрим примеры.
Найти площадь фигуры, ограниченной линиями (5.1-5.6)
5.1. y = , y =
, y =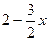 .
.
5.2. y =tg x, y = cos x, x =0.
cos x, x =0.
5.3. y =2 x 2, y = .
.
5.4. y =ln(x +6), y =3ln x, y =0.
5.5. x = y 2, x =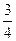 y 2+1,
y 2+1,
5.6. y =2 x -3+1, y =23- x +1, y =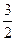 .
.
 Решение.
Решение.
5.1. Найдём точки пересечения графиков функций:
 =
=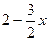 , x 2+3 x -4=0, x 1=-4, x 2=1.
, x 2+3 x -4=0, x 1=-4, x 2=1.
Вычисляем площадь
S =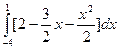 =
= =
= =
=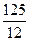 .
.
5.2. Найдём точку пересечения графиков функций
 tg x =
tg x = cos x, 3sin x =2cos2 x.
cos x, 3sin x =2cos2 x.
Сделаем замену неизвестной sin x = z. Тогда 2-2 z 2=3 z, 2 z 2+3 z -2=0. Решая уравнение, находим, z 1=-2, z 2=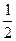 . Решение z =-2 постороннее. Решаем далее,sin x =
. Решение z =-2 постороннее. Решаем далее,sin x =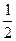 , x =
, x =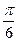 .
.
Находим площадь
S = =
=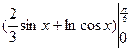 =
=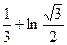 .
.
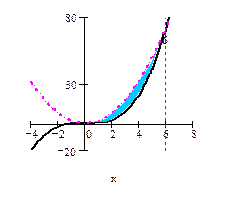 5.3. Ищем точку пересечения графиков
5.3. Ищем точку пересечения графиков
функций
2 x 2= , x 1=0, x 2=6.
, x 1=0, x 2=6.
При 0≤ x ≤6 имеем  ≤2 x 2. Поэтому
≤2 x 2. Поэтому
S =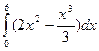 =
=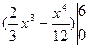 =36.
=36.
5.4. Ищем точку пересечения графиков функций
ln(x +6)=3ln x = ln x 3, x +6= x 3.
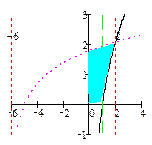 Ясно, что x =2. Находим площадь фигуры.
Ясно, что x =2. Находим площадь фигуры.
S =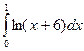 +
+ .
.
Интегралы вычисляем с помощью формулы интегрирования по частям. Для первого интеграла полагаем u = ln(x +6), du =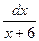 , v = x; для второго u = ln(x +6)-3ln x, du =
, v = x; для второго u = ln(x +6)-3ln x, du =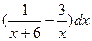 , v = x.
, v = x.
Получаем
S = -
-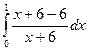 +
+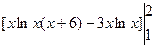 -
-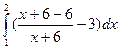 =ln7-
=ln7-
-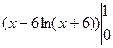 +2ln8-6ln2-ln7-
+2ln8-6ln2-ln7-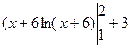 =-1+6 ln7-6 ln6+
=-1+6 ln7-6 ln6+ -2-
-2-
-6ln8+1+6ln7+3=1+12 ln7-6 ln48=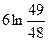 +1.
+1.

5.5. В этой задаче мы рассмотрим в качестве функции x, а y будет аргументом. Ищем точки пересечения графиков функций y 2=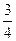 y 2+1. Находим y1=-2, y 2=2. Вычисляем площадь
y 2+1. Находим y1=-2, y 2=2. Вычисляем площадь
S =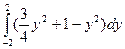 =
=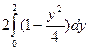 =
= =
=
|
|
|
2(2- )=
)= .
.
При вычислении интеграла по отрезку [-2,2] мы учли чётность функции x = .
.
 5.6. Здесь, как и в предыдущей задаче, удобнее считать y аргументом, а x - функцией. Тогда при вычислении площади нам потребуется только один интеграл, в то время как при вычислении площади фигуры, ограниченной графиками y 1=2 x -3+1, y 2=23- x +1, y 3=
5.6. Здесь, как и в предыдущей задаче, удобнее считать y аргументом, а x - функцией. Тогда при вычислении площади нам потребуется только один интеграл, в то время как при вычислении площади фигуры, ограниченной графиками y 1=2 x -3+1, y 2=23- x +1, y 3=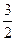 , понадобится два интеграла, что хорошо видно из рисунка.
, понадобится два интеграла, что хорошо видно из рисунка.
Найдём выражение x через y. Получаем, x 1=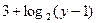 , x 2=
, x 2= ,
, 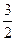 ≤ y ≤2, так как точкой пересечения графиков функций x 1=
≤ y ≤2, так как точкой пересечения графиков функций x 1=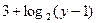 и x 2=
и x 2= будет точка (3,2).
будет точка (3,2).
Вычисляем площадь фигуры
S = =
= .
.
Вычислим интеграл, применяя формулу интегрирования по частям, полагая u = , du =
, du =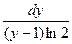 , v = y -1. Тогда
, v = y -1. Тогда
S =-2[ -
- ]= -2[0-
]= -2[0-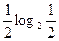 -
- ]=-2[
]=-2[ -
- ]=
]=
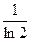 -1=
-1= .
.
 5.7. Найти площадь фигуры, ограниченной параболой y = - x 2-2 x +3, касательной к ней в точке М (2,-5) и осью ординат.
5.7. Найти площадь фигуры, ограниченной параболой y = - x 2-2 x +3, касательной к ней в точке М (2,-5) и осью ординат.
Решение. Найдём уравнение касательной y ¢=-2 x -2, y ¢(2)=-6. Тогда y +5=-6(x -2) - уравнение касательной, проходящей через точку М (2,-5). Перепишем уравнение в виде y = -6 x +7.
Вычислим площадь фигуры
S =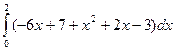 =
= =
=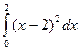 =
=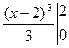 =0-(-
=0-(-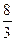 )=
)=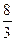 .
.
Вычислить площади криволинейных трапеций, образованных графиками функций
(5.8-5.9)
5.8. y = , x Î[0,1).
, x Î[0,1).
5.9. y =4 e - x, x Î[0,¥).
Решение.
5.8. При x Î[0,1) 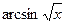 ≥0 и, следовательно
≥0 и, следовательно
S = =
= =
= =
= =
=
=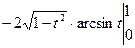 +
+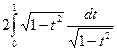 =2.
=2.
Отметим, что в этом примере площадь вычислена с помощью несобственного интеграла.
5.9. Имеем
S = .
.
Вычислим интеграл с помощью формулы интегрирования по частям, применённой несколько раз. Воспользуемся обобщённой формулой интегрирования по частям (см. п. главы I). Положим u = x 4. Тогда u ¢=4 x 3, u ¢¢=12 x 2, u ¢¢¢=24 x,  =24. Далее v = e - x , v 1=
=24. Далее v = e - x , v 1=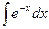 =
=
= - e - x , v 2=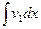 = e - x , v 3= - e - x , v 4= e - x .
= e - x , v 3= - e - x , v 4= e - x .
Получим
S = =
=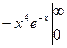 -
-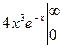 -
-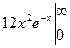 -
-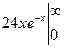 +
+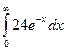 .
.
Поскольку  , m =1,2,… (это доказывается последовательным применением правила Лопиталя), то мы получаем
, m =1,2,… (это доказывается последовательным применением правила Лопиталя), то мы получаем
S = =
=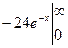 =24.
=24.
24. Найти площадь фигуры, ограниченной кривыми, заданными в полярных координатах (5.10-5.14).
5.10. r = a cos3 j (a =2).
5.11. r = 2- cos j, r = cos j.
5.12. r = , r =
, r =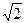 (внутри окружности).
(внутри окружности).
5.13. r =2 j, j = 0 (0≤ j ≤2 π).
5.14. r 2= 4cos2 j, r 2= 4sin2 j (пересечение областей, ограниченных этими кривыми).
|
|
|
Решение.
5.10. Так как функция r = a cos3 j имеет период T =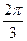 , то при изменении j от 0 до 2 π радиус-вектор описывает три равных лепестка кривой. Допустимыми для j являются те значения при которых cos3 j ≥0, откуда
, то при изменении j от 0 до 2 π радиус-вектор описывает три равных лепестка кривой. Допустимыми для j являются те значения при которых cos3 j ≥0, откуда
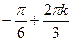 ≤ j ≤
≤ j ≤ , k =0, ±1, ±2,….
, k =0, ±1, ±2,….
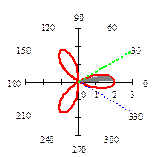 При k = 0 имеем первый лепесток, соответствующий -
При k = 0 имеем первый лепесток, соответствующий -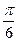 ≤ j ≤
≤ j ≤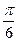 . При k = 1 получаем пределы для j, соответствующие второму лепестку,
. При k = 1 получаем пределы для j, соответствующие второму лепестку,  ≤ j ≤
≤ j ≤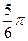 . Если k = 2, то третий лепесток линии соответствует изменениям j:
. Если k = 2, то третий лепесток линии соответствует изменениям j: 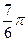 ≤ j ≤
≤ j ≤ . В этих трёх промежутках заключена кривая, соответствующая изменению j от 0 до 2 π (полный оборот). Если брать k = 3, 4,…, то мы не получим новой линии, а будем каждый раз проходить одну и ту же линию.
. В этих трёх промежутках заключена кривая, соответствующая изменению j от 0 до 2 π (полный оборот). Если брать k = 3, 4,…, то мы не получим новой линии, а будем каждый раз проходить одну и ту же линию.
Поскольку лепестки одинаковы, то достаточно найти площадь одного из них и затем утроить.
Имеем
S =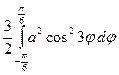 =3 a 2
=3 a 2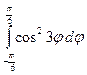 =
=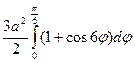 =
= =
=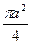 .
.
При вычислении интеграла мы учли чётность функции cos23 j.
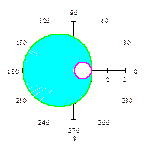 5.11. r = cos j - это уравнение окружности (x -
5.11. r = cos j - это уравнение окружности (x -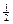 )2+ y 2=
)2+ y 2= в полярных координатах. Найдём площадь фигуры между линией r = 2- cos j и окружностью. Ясно, что площадь фигуры есть разность площадей, ограниченных двумя линиями:
в полярных координатах. Найдём площадь фигуры между линией r = 2- cos j и окружностью. Ясно, что площадь фигуры есть разность площадей, ограниченных двумя линиями:
S = S 1- S 2, где S 1=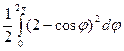 , S 2=
, S 2=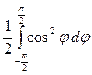 .
.
Вычисляем эти интегралы.
S 1= =
=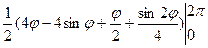 =
=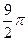 .
.
S 2=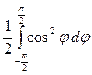 =
=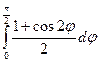 =
= =
=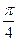 .
.
Окончательно получаем S = 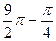 =
=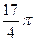 .
.
При вычислении S 2 мы использовали чётность функции cos2 j.
5.12. Найдём все значения j, при которых cos2 j ≥0. Имеем
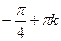 ≤ j ≤
≤ j ≤ , k =0, ±1, ±2,….
, k =0, ±1, ±2,….
При k = 0 получаем 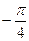 ≤ j ≤
≤ j ≤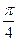 , при k = 1:
, при k = 1:  ≤ j ≤
≤ j ≤ . Далее при k = 2, 3, … мы будем получать один из этих двух лепестков. Итак, фигура ограничена двумя одинаковыми лепестками. Нас интересует площадь фигуры внутри окружности r =
. Далее при k = 2, 3, … мы будем получать один из этих двух лепестков. Итак, фигура ограничена двумя одинаковыми лепестками. Нас интересует площадь фигуры внутри окружности r =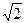 .
.
Найдём полярные координаты точек пересечения кривой r = с окружностью r =
с окружностью r =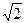 . Решая уравнение
. Решая уравнение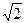 =
= , получаем j =
, получаем j = 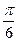
 , k = 0,±1, …
, k = 0,±1, …
 Выберем значения j из отрезка [- π, π ], такие что cos2 j ≥0. Ясно, что достаточно рассмотреть
Выберем значения j из отрезка [- π, π ], такие что cos2 j ≥0. Ясно, что достаточно рассмотреть  =
=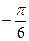 ,
, 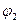 =
=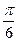 , что соответствует первому лепестку. Вычислим соответствующую площадь и удвоим её, что даст нам искомую площадь. Имеем
, что соответствует первому лепестку. Вычислим соответствующую площадь и удвоим её, что даст нам искомую площадь. Имеем
S = +
+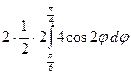 =
= +
+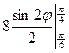 =
= +4(
+4(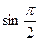 -
-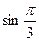 )=
)= +4-2
+4-2 .
.
При вычислении второго интеграла мы учли симметрию фигуры относительно полярной оси.
 5.13. Линия r =2 j - спираль, раскручивающаяся из начала координат O. Нам требуется определить площадь, ограниченную одним витком спирали и полярной осью.
5.13. Линия r =2 j - спираль, раскручивающаяся из начала координат O. Нам требуется определить площадь, ограниченную одним витком спирали и полярной осью.
Вычисляем площадь.
S =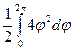 =
= =
=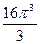 .
.
5.14. Линия r 2= 4cos2 j представляет из себя два одинаковых лепестка. Одному из
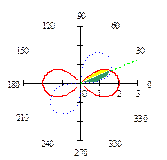 них соответствуют углы
них соответствуют углы 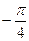 ≤ j ≤
≤ j ≤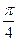 , другому
, другому  ≤ j ≤
≤ j ≤ . Линия r 2= 4sin2 j образует два равных лепестка, один вписан в угол
. Линия r 2= 4sin2 j образует два равных лепестка, один вписан в угол  ≤ j ≤
≤ j ≤ , второй - в угол π ≤ j ≤
, второй - в угол π ≤ j ≤ . Найдём точки пересечения линий.
. Найдём точки пересечения линий.
|
|
|
4sin2 j = 4cos2 j,  =
=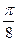 ,
,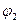 =
= .
.
Луч j =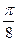 делит часть нашей области в первом квадрате пополам, луч j =
делит часть нашей области в первом квадрате пополам, луч j = делает то же самое с частью области в третьем квадрате. Достаточно найти площадь части
делает то же самое с частью области в третьем квадрате. Достаточно найти площадь части
0≤ r ≤ ,
, 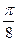 ≤ j ≤
≤ j ≤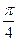 ,
,
и умножить на четыре. Это и будет искомое решение. Вычисляем
S =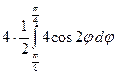 =
= =4(
=4(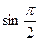 -
- )=4(1-
)=4(1-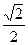 )=2(2-
)=2(2-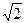 ).
).
Перейдя к полярным координатам, найти площадь области, ограниченной кривыми (5.15-5.16)
5.15. x 2+ y 2=6 x, x 2+ y 2=6 y, точка M (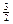 ,
,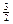 ) принадлежит области.
) принадлежит области.
5.16. x 2+ y 2=9, x 2+ y 2=2 x,
x,  x + y =0,
x + y =0,  x - y =0 (x >0, x 2+ y 2≤9).
x - y =0 (x >0, x 2+ y 2≤9).
Решение.
 5.15. Линии являются окружностями (x -3)2+ y 2=9 и x 2+(y -3)2=9. Пересечение кругов делится биссектрисой y = x первого квадранта на две равные части. Найдём площадь одной, затем удвоим.
5.15. Линии являются окружностями (x -3)2+ y 2=9 и x 2+(y -3)2=9. Пересечение кругов делится биссектрисой y = x первого квадранта на две равные части. Найдём площадь одной, затем удвоим.
В полярных координатах x = r cos j, y = r sin j, уравнение x 2+ y 2=6x окружности принимает вид r = 6cos j, уравнение второй окружности имеет вид r = 6sin j. Вычисляем площадь.
S = =18
=18 =
= =
=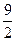 (π -2).
(π -2).
 5.16. Перейдём к полярным координатам x = r cos j, y = r sin j. Тогда граница области будет задаваться уравнениями r = 3, r = 2
5.16. Перейдём к полярным координатам x = r cos j, y = r sin j. Тогда граница области будет задаваться уравнениями r = 3, r = 2 cos j, j = -
cos j, j = -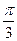 , j =
, j = 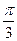 .
.
Наша область - фигура, симметричная относительно полярной оси (оси O x). Найдём площадь заштрихованной области и результат удвоим. Получим искомый ответ.
Полярные координаты точки пересечения окружностей находятся из уравнения 3 = 2 cos j, cos j =
cos j, cos j =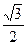 , j =±
, j =±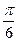 . Вычисляем площадь.
. Вычисляем площадь.
S =2( +
+ )=
)=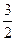 π + 6
π + 6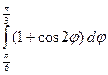 =
= 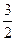 π + π +3
π + π +3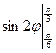 =
= +3×
+3×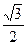 -3×
-3×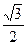 =
= .
.
25. Найти площадь фигуры, ограниченной кривой, заданной параметрически (5.17-5.18).
5.17. x = a cos t, y = b sin t.
5.18. x = 3 sin t, y = 3 sin2 t.
Решение.
5.17. Данная линия есть эллипс 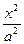 +
+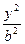 =1. Используя формулу для вычисления площади, находим
=1. Используя формулу для вычисления площади, находим
S =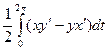 =
= =
=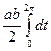 = π ab.
= π ab.
 5.18. Выражая y через x, получаем
5.18. Выражая y через x, получаем
y =±2 x 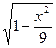 т.е. кривая симметрична относительно осей ОХ, ОУ.
т.е. кривая симметрична относительно осей ОХ, ОУ.
При t Î[0, ] x ≥0 и y =2 x
] x ≥0 и y =2 x 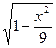 ≥0, график в первом квадрате - четвертая часть всей кривой. При изменении t от 0 до π точка (x, y) описывает на плоскости x O y замкнутую кривую, симметричную относительно оси O x. При изменении t от π до 2 π x изменяется сначала от 0 до -3
≥0, график в первом квадрате - четвертая часть всей кривой. При изменении t от 0 до π точка (x, y) описывает на плоскости x O y замкнутую кривую, симметричную относительно оси O x. При изменении t от π до 2 π x изменяется сначала от 0 до -3
(t изменяется от π до  ), затем от -3 до 0 (
), затем от -3 до 0 ( ≤ t ≤2 π). Ордината y = 2 x
≤ t ≤2 π). Ордината y = 2 x 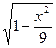 ≥0 - при t Î[ π,
≥0 - при t Î[ π,  ] и y = 2 x
] и y = 2 x 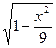 ≤0 при t Î[
≤0 при t Î[  , π ], то есть, при изменении t от π до 2 π мы получаем снова замкнутую кривую, симметричную первой кривой относительно оси ординат.
, π ], то есть, при изменении t от π до 2 π мы получаем снова замкнутую кривую, симметричную первой кривой относительно оси ординат.
|
|
|
Мы найдём площадь фигуры, соответствующей изменению t от 0 до  , а затем умножим результат на четыре. Это и даст нам искомый ответ. Вычисляем
, а затем умножим результат на четыре. Это и даст нам искомый ответ. Вычисляем
S =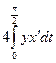 =
=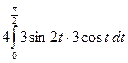 =
=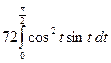 =
= =
=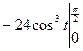 =24.
=24.
26. Вычисление длины кривой. Основные формулы.
Если плоская кривая задана как график функции y = f (x), a ≤ x ≤ b, и производная y¢ = f¢ (x) непрерывна, то длина дуги этой кривой выражается интегралом
l =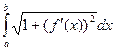 =
=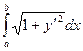 .
.
Если кривая задана параметрически x = x (t), y = y (t), a ≤ t ≤ b, и производные x¢ (t) и y¢ (t) непрерывны на отрезке [ a, b ], то длина дуги кривой выражается интегралом
l =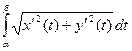 .
.
Если кривая задана уравнением r = r (j), a ≤ j ≤ b, в полярных координатах и r¢ (j) непрерывна на отрезке [ a, b ], то длина l дуги кривой выражается интегралом
l =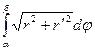 .
.
Если Г - пространственная кривая, заданная параметрически: x = x (t), y = y (t), z = z (t), a ≤ t ≤ b, производные x¢ (t), y¢ (t) и z¢ (t) непрерывны на отрезке [ a, b ], то длина Г выражается по формуле
l = .
.
Замечание. Пусть Г - некоторая кривая на плоскости x O y. Выражение
dl = ,
,
где dx 2=(dx)2, dy 2=(dy)2, называется дифференциалом длины дуги. Используя это понятие, можно единообразно записать формулу для вычисления длины кривой
l = =
=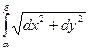 ,
,
где a и b (a ≤ b), обозначают границы изменения параметра, с помощью которого задаётся кривая. Пусть кривая Г есть график функции x = x (y), c≤ y ≤ d. Тогда dx = x¢ (y)dy и мы получаем
l = =
=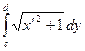 .
.
Если кривая Г задана параметрически, то dx = x¢ (t)dt, dy = y¢ (t)dt и мы получаем
l =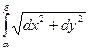 =
= =
= .
.
Задание кривой с помощью полярных координат: r = r (j), a ≤ j ≤ b, есть частный случай параметрического задания: x = r (j)cos j, y = r (j)sin j. Параметром здесь является j. Вычисляя дифференциалы dx = (r ¢ cos j - r sin j) dj, dy = (r ¢sin j + r cos j) dj, убеждаемся, что
dl = =
= .
.
Для пространственной кривой Г дифференциалом длины дуги называется выражение
dl =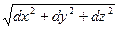 .
.
Длину кривой Г можно выразить интегралом
l = =
= ,
,
где a и b (a ≤ b) - концы отрезка [ a, b ] - промежутка изменения параметра, с помощью которого задаётся кривая.
27. Рассмотрим примеры.
Вычислить длину дуги кривой (5.19-5.24).
5.19. y = 1-ln cos x, 0≤ x ≤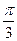 .
.
5.20. y = 2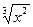 , 0≤ x ≤1.
, 0≤ x ≤1.
5.21. x = 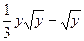 , 0≤ y ≤4.
, 0≤ y ≤4.
5.22. 3 y 2 = x (x -1)2 (длину петли).
5.23. y = 2(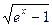 -
- ),0≤ x ≤ ln4.
),0≤ x ≤ ln4.
5.24. y =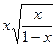 , 0≤ x ≤
, 0≤ x ≤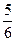 .
.
Решение.
5.19. Так как y ¢ =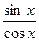 = tg x, то
= tg x, то
l = =
=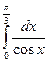 =
= =
= =
= =
=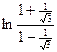 = =
= =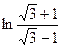 = ln(2+
= ln(2+ ).
).
5.20. y’ =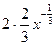 ,
,
l =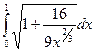 =
= =
=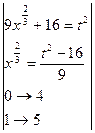 =
= =
=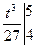 =
=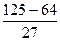 =
=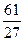 .
.
Можно было рассмотреть нашу кривую как график функции  ,
,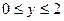 . Тогда вычисление длины кривой свелось бы к нахождению интеграла
. Тогда вычисление длины кривой свелось бы к нахождению интеграла
l =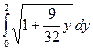 .
.
5.21. Вычисляем производную  =
= и далее
и далее 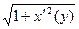 =
= =
=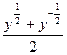 , откуда
, откуда
l =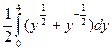 =
=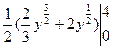 =
=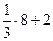 =
=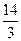 .
.
5.22. Из условия следует, что y =0 при x =0 и x =1. Линия симметрична относительно оси O x, так как y входит в уравнение в чётной степени. Вычислим длину половины петли, задаваемой уравнением y = ,
, 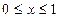 . (Вторая половина петли есть график функции y = -
. (Вторая половина петли есть график функции y = - ). Так как
). Так как  ,
,  =
=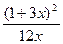 , то получаем
, то получаем
l =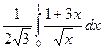 =
=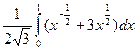 =
=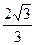 .
.
5.23. Делаем предварительные вычисления.
 =
=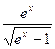 -
- =
=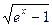 .
.
Вычисляем длину кривой l =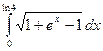 =
=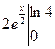 =
=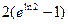 =2.
=2.
5.24. Вычисляем производную: =
=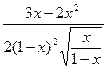 тогда
тогда
 =
= =
= .
.
Вычисляем длину кривой
l = =
=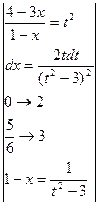 =
=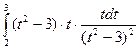 =
=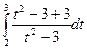 =
=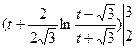 =
=
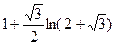 .
.
Вычислить длину кривой, заданной в полярных координатах (5.25-5.28).
5.25. r = , -
, -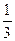 ≤ j ≤
≤ j ≤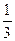 .
.
5.26. r = a (1+cos j), 0 ≤ j ≤ 2 π (кардиоида).
5.27. r =th , 0 ≤ j ≤ 2.
, 0 ≤ j ≤ 2.
5.28. r = acos4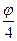 .
.
Решение.
5.25. Вычисляем длину кривой по формуле
l = =
=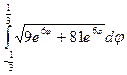 =
= =
= =
=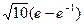 =
=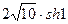 .
.
5.26. l = =
=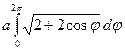 =
=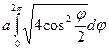 =
= =
=
= -
-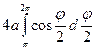 =
= -
- =4 a +4 a =8 a.
=4 a +4 a =8 a.
5.27.
l =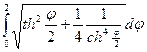 =
= =
= =
= = =
= =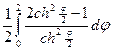 =
= =
= =
= =1-th1.
=1-th1.
 5.28. Функция cos
5.28. Функция cos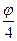 имеет период 8 π. Функции | cos
имеет период 8 π. Функции | cos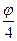 |, cos2
|, cos2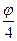 , cos4
, cos4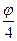 и т.п. имеют период 4 π. Поскольку cos(-
и т.п. имеют период 4 π. Поскольку cos(-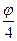 ) = cos
) = cos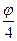 , то линия симметрична относительно полярной оси и при изменении j от 0 до 2 π полярный радиус опишет половину линии. Найдём длину половины кривой (на рисунке) и затем удвоим результат. Вычисляем
, то линия симметрична относительно полярной оси и при изменении j от 0 до 2 π полярный радиус опишет половину линии. Найдём длину половины кривой (на рисунке) и затем удвоим результат. Вычисляем
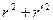 = a 2[
= a 2[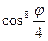 +
+ ]=
]=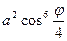 .
.
Отсюда следует
l = =
=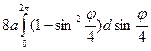 =
=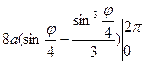 =8 a (1-
=8 a (1-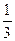 )=
)= .
.
Вычислить длину кривой, заданной параметрически (5.29-5.33).
5.29. x = 6 t 5, y = 5 t (1- t 8), 0≤ t ≤1.
5.30. x = ln(1+ t 2), y = 2arctg t -2 t +8, 0≤ t ≤1.
5.31. x = t -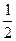 sh2 t, y = 2ch t, 0≤ t ≤1.
sh2 t, y = 2ch t, 0≤ t ≤1.
5.32. x = 2cos3 t, y = 2sin3 t.
5.33. x =  t 2, y = t - t 3 (длину петли).
t 2, y = t - t 3 (длину петли).
Решение.
5.29. Вычисляем, используя соответствующую формулу
l =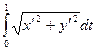 =
= =5
=5 =5
=5 = =
= =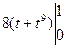 =16.
=16.
5.30.  =
=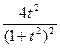 +
+ =
=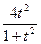 . Поэтому
. Поэтому
l = =
=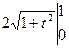 =2(
=2(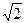 -1).
-1).
5.31.  =(1-ch2 t)2+4sh2 t =|ch2 t -1=2sh2 t |=4sh4 t +4sh2 t =|1+sh2 t =ch2 t |=4 sh2 t ch2 t = =sh22 t.
=(1-ch2 t)2+4sh2 t =|ch2 t -1=2sh2 t |=4sh4 t +4sh2 t =|1+sh2 t =ch2 t |=4 sh2 t ch2 t = =sh22 t.
Поэтому
l =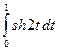 =
= =
=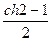 = sh21.
= sh21.
5.32. Уравнение линии (астроиды) в декартовых координатах имеет вид
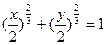 или
или  .
.
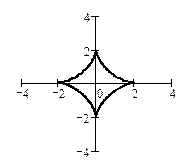 Отсюда следует, что линия симметрична относительно обеих осей координат. Вычислим четверть длины астроиды, что соответствует изменению параметра t от 0 до
Отсюда следует, что линия симметрична относительно обеих осей координат. Вычислим четверть длины астроиды, что соответствует изменению параметра t от 0 до  , и результат учетверим. Вычисляем
, и результат учетверим. Вычисляем
 =36cos4 t sin2 t +36 sin4 t cos2 t =36 sin2 t cos2 t =9 sin22 t.
=36cos4 t sin2 t +36 sin4 t cos2 t =36 sin2 t cos2 t =9 sin22 t.
Отсюда следует
l =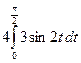 =
= =6+6=12.
=6+6=12.
5.33. Если выразить y через x, то мы получаем y = 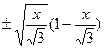 , откуда следует, что при x Î[0,
, откуда следует, что при x Î[0, ] графики симметричных относительно оси O x функций y =
] графики симметричных относительно оси O x функций y = 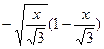 и y =
и y = 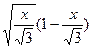 образуют замкнутый контур на плоскости x O y (петлю). График функции y =
образуют замкнутый контур на плоскости x O y (петлю). График функции y = 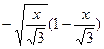 получается, когда t изменяется от -1 до 0, а при изменении t от 0 до 1 точка (x, y) движется по графику функции y =
получается, когда t изменяется от -1 до 0, а при изменении t от 0 до 1 точка (x, y) движется по графику функции y = 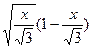 от точки O (0,0) до точки A(
от точки O (0,0) до точки A( ,0).
,0).
Вычисляем сначала  =12 t 2+(1-3 t 2)2=(1+3 t 2)2.
=12 t 2+(1-3 t 2)2=(1+3 t 2)2.
Поэтому
l = =
=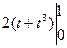 =4.
=4.
Вычислить длину дуги пространственной кривой (5.34-5.37)
5.34. x =3 t - t 3, y =3 t 2, z =3 t + t 3, 0≤ t ≤1.
5.35. x = at, y =  , z =
, z =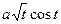 ,
,  ≤ t ≤1.
≤ t ≤1.
5.36. x = et, y = e-t, z =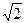 t, 0≤ t ≤2.
t, 0≤ t ≤2.
5.37. x = a (1+cos t), y = a (t -sin t), z =4 a sin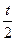 , 0≤ t ≤2.
, 0≤ t ≤2.
Решение.
5.34. Вычисляем длину кривой по формуле
l = =
= =
=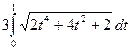 =
= =
= =4
=4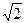 .
.
5.35.  =
=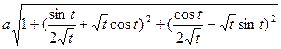 =
= =
=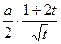 =
=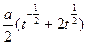 .
.
Отсюда получаем
l = =
= =
=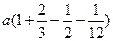 =
= .
.
5.36. Имеем  = e 2 t + e- 2 t +2 =(et + e-t)2. Откуда получаем
= e 2 t + e- 2 t +2 =(et + e-t)2. Откуда получаем
l =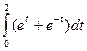 =
= =
= =2 sh 2.
=2 sh 2.
5.37. Сделаем предварительные вычисления.
 = a 2[sin2 t +(1-cos t)2+4
= a 2[sin2 t +(1-cos t)2+4 ]= a 2[2(1-cos t)+4
]= a 2[2(1-cos t)+4 ]=4 a 2.
]=4 a 2.
Мы использовали здесь тригонометрическую формулу 1- cos t = . Вычисляем длину кривой l =
. Вычисляем длину кривой l =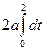 =4 a.
=4 a.
28. Вычисление объёмов и площадей поверхностей. Основные формулы.
Пусть S (x) - площадь сечения тела V плоскостью, перпендикулярной к оси O x в точке с абсциссой x, a и b - левая и правая границы изменения x. Тогда объём тела V выражается интегралом
V =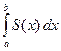 .
.
Если тело V образовано вращением вокруг оси O x криволинейной трапеции, ограниченной кривой y = f (x)≥0, a ≤ x ≤ b, осью абсцисс и прямыми x = a, x = b, то объём тела V вычисляется по формуле
V = =
= .
.
Если тело образовано вращением вокруг оси O y криволинейной трапеции, образованной под графиком функции x = g (y), c ≤ y ≤ d (g (y)≥0), то объём тела выражается интегралом
V = =
= .
.
Если вокруг оси O y вращается криволинейная трапеция, ограниченная графиком функции y = f (x)≥0, a ≤ x ≤ b, осью абсцисс и прямыми x = a, x = b, то объём получившегося тела выражается интегралом
V = =
=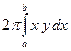 .
.
Если кривая задана параметрически или в полярных координатах, то следует сделать соответствующую замену переменных в указанных выше формулах.
Площадь поверхности, образованной вращением вокруг оси O x дуги Г кривой y = f (x), a ≤ x ≤ b, где f (x) имеет на отрезке [ a, b ] непрерывную производную  , выражается интегралом
, выражается интегралом
S = =
=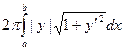 .
.
Поскольку 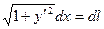 - дифференциал длины дуги, то формулу можно записать в виде
- дифференциал длины дуги, то формулу можно записать в виде
S = .
.
Пусть кривая задана параметрически, x = x (t), y = y (t), a ≤ t ≤ b, где функции x (t) и y (t) имеют на отрезке [ a, b ] непрерывные производные x ¢(t) и y ¢(t). Площадь S поверхности, образованной при вращении данной кривой вокруг оси O x равна
S =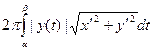 =
= .
.
Задание кривой с помощью полярных координат r = r (j), a ≤ j ≤ b, есть частный случай параметрического задания, так как в этом случае
x = r (j) cos j, y = r (j) sin j.
29. Рассмотрим примеры.
 5.38. На всех хордах круга радиуса R, параллельных одному направлению, построены симметричные параболические сегменты постоянной высоты h. Плоскости сегментов перпендикулярны к плоскости круга. Найти объём образованного таким образом тела.
5.38. На всех хордах круга радиуса R, параллельных одному направлению, построены симметричные параболические сегменты постоянной высоты h. Плоскости сегментов перпендикулярны к плоскости круга. Найти объём образованного таким образом тела.
 Решение. Найдём в начале площадь параболического сегмента с основанием a и высотой h. (см. рис. б). Расположим оси координат так, что основание сегмента будет находиться на оси абсцисс и начало координат делит это основание пополам.
Решение. Найдём в начале площадь параболического сегмента с основанием a и высотой h. (см. рис. б). Расположим оси координат так, что основание сегмента будет находиться на оси абсцисс и начало координат делит это основание пополам.
Уравнение параболы имеет вид y = a (x - )(x +
)(x + )= a (x 2-
)= a (x 2-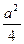 ). Так как y (0)= h, то a = -
). Так как y (0)= h, то a = - . Тогда уравнение параболы принимает вид y = -
. Тогда уравнение параболы принимает вид y = -  (x 2-
(x 2-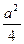 ). Ищем площадь сегмента
). Ищем площадь сегмента
S =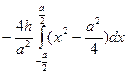 =
=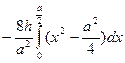 =
= =
= ah.
ah.
Расположим оси координат так, как показано на рис. а. Тогда длина половины хорды, пересекающей ось абсцисс в точке x есть  .
.
Следовательно, площадь параболического сегмента, соответствующего значению x, равна S (x)=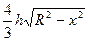 . Согласно формуле для объёма, получаем
. Согласно формуле для объёма, получаем
V = =
= =
= =
=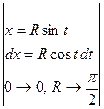 =
=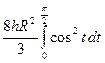 ==
== .
.
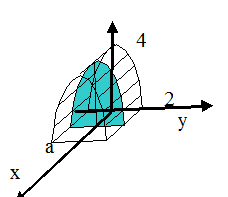 5.39. Найти объём тела, ограниченного поверхностями z = 4- y 2, x =0, x = a, y =0, z =0.
5.39. Найти объём тела, ограниченного поверхностями z = 4- y 2, x =0, x = a, y =0, z =0.
Решение. Найдём площадь сечения тела плоскостью, перпендикулярной оси O x (0≤ x ≤ a). Нам необходимо знать площадь половины параболического сегмента с a =2, h =4. Как мы знаем из решения предыдущей задачи, эта площадь равна
S (x)=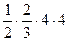 =
= , 0≤ x ≤ a.
, 0≤ x ≤ a.
Отсюда получаем
V =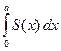 =
=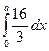 =
=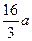 .
.
Найти объём тела, образованного вращением фигуры, ограниченной линиями (5.40-5.51)
5.40. y = sin x, x = 0, 0≤ x ≤ π, вокруг оси а) O x, б) O y.
5.41. y = 2 x, y =  , x =0, y =0, вокруг оси O x.
, x =0, y =0, вокруг оси O x.
5.42. y = x (3- x), y = x, вокруг оси а) O x, б) O y.
5.43. y = cos x, y =1, 0 ≤ x ≤ 2 π, вокруг оси O y.
5.44. y = ex +6, y = e 2x, x =0, вокруг оси а) O x, б) O y.
5.45. y =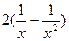 , y =0, x ≥1, вокруг оси O x.
, y =0, x ≥1, вокруг оси O x.
5.46. y = , y =0, x ≥0, вокруг оси O x.
, y =0, x ≥0, вокруг оси O x.
5.47. y = , y =0, вокруг оси O y.
, y =0, вокруг оси O y.
5.48.
Дата добавления: 2014-01-20; Просмотров: 4328; Нарушение авторских прав?; Мы поможем в написании вашей работы!