Разностные уравнения второго порядка

Займёмся теперь линейными разностными уравнениями второго порядка. Самый общий вид линейного разностного уравнения второго порядка следующий

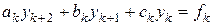. (5.4)

Соответствующее однородное уравнение записывается в виде

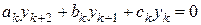. (5.5)

Для линейных разностных уравнений можно развить теорию аналогичную теории для линейных дифференциальных уравнений.

Перейдём к рассмотрению частного случая линейных разностных уравнений – линейных разностных уравнений с постоянными коэффициентами. В этом случае уравнение второго порядка имеет вид

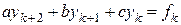. (5.6)

Соответствующее однородное уравнение записывается в виде

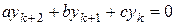. (5.7)

По аналогии с уравнениями первого порядка с постоянными коэффициентами будем искать решение уравнения (5.7) в виде 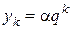. Подставляя это решение в (5.7), получаем 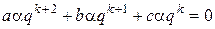, или, сокращая на 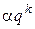, получаем 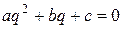. Таким образом, мы доказали, что для того чтобы 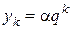было решением уравнения (5.7), нужно (необходимо), чтобы 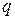было решением алгебраического (в данном случае квадратного) уравнения 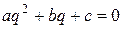. Рассмотрим возникающие здесь возможности.

1. Оба корня данного квадратного уравнения действительны и различны. Тогда мы имеем два линейно независимых решения 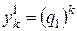и 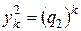уравнения (5.7). Тогда общее решение уравнения (5.7) будет иметь вид .

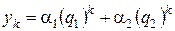2. Корни одинаковые, в этом случае говорят, что квадратное уравнение имеет корень кратности 2. Тогда, по аналогии с линейными дифференциальными уравнениями второго порядка можно доказать, что решения 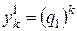и 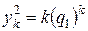линейно независимы и общее решение уравнения (5.7) имеет вид .

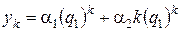3. Корни комплексные. Если коэффициенты уравнения действительны, то тогда эти корни являются комплексно сопряжёнными, то есть имеют вид 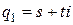, 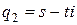. Соответственно решения 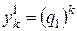и 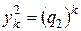уравнения (5.7) будут линейно независимы. Записав 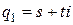, 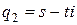в тригонометрической форме, то есть в ви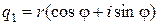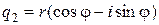де , , где 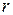‑ модуль, а 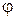‑ аргумент числа 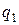, получаем 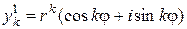и 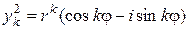. По теореме о наложении решений можем утверждать, что линейные комбинаци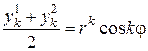и и 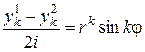тоже являются решениями уравнения (5.7), причём линейно независимыми. Тогда общее решение уравнения (5.7) может быть записано в виде .

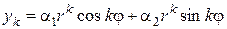Пример 3. Решить уравнение .

Решениями характеристического уравнения 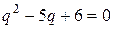являются 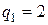, 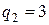. Поэтому имеем два линейно независимых решения 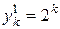и нашего уравнения . Тогда общее решение данного уравнения имеет вид .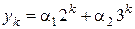

Пример 4. Решить уравнение .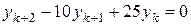

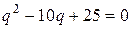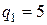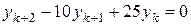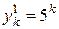Решением характеристического уравнения является кратности 2. Следовательно двумя линейно независимыми решениями уравнения будут и 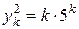. Тогда общее решение данного уравнения имеет вид .

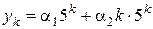Пример 5. Решить уравнение .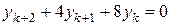

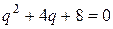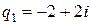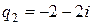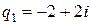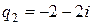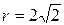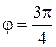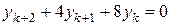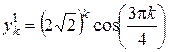Решениями характеристического уравнения являются комплексно сопряжённые числа , . Модули комплексных чисел и равен , а аргумент ‑ . Тогда два линейно независимых решения уравнения равны и 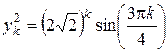, а общее решение данного уравнения имеет вид .

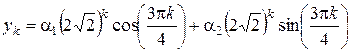Аналогичная теория может быть построена и для линейных разностных уравнений порядка . Самый общий вид линейного разностного уравнения порядка следующий

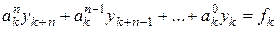. (5.8)

Соответствующее однородное уравнение записывается в виде

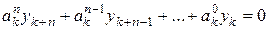. (5.9)

Для частного случая линейных разностных уравнений – линейных разностных уравнений с постоянными коэффициентами можем записать

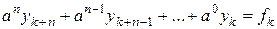. (5.10)

Соответствующее однородное уравнение записывается в виде

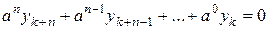. (5.7)

Дата добавления: 2014-01-11