Т2. Пусть функции и непрерывны на интервале и удовлетворяют неравенству , а в точке обе функции терпят разрыв II рода. Тогда из сходимости интеграла вытекает

Т2. Пусть функции и непрерывны на интервале и удовлетворяют неравенству. Тогда из сходимости интеграла вытекает сходимость интеграла, а из расходимости интеграла следует расходимость интеграла.

.

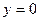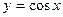Пример 2. Вычислить площадь плоской фигуры, ограниченной линиями и при .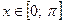

Заданные линии определяют полуволну косинусоиды, которая изменяет свой знак с “+” на “–” в точке 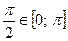. Следовательно, площаль такой плоской фигуры будет равна (Рис. 9):

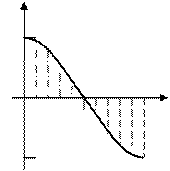
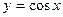Рис. 9. Площадь плоской фигуры, ограниченной

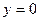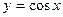линиями и при .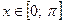

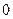
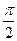
– 1

.

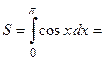
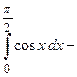
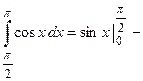
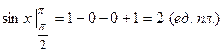4. Пусть функци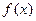и и 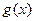непрерывны на сегменте 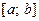и на этом отрезке удовлетворяют неравенству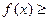 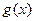(Рис. 10), тогда площадь криволинейной трапеции можно вычислить по формуле

.

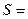
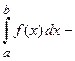
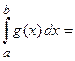
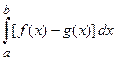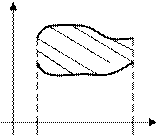
Рис. 10. Площадь плоской фигуры, ограниченной

линиям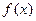и и 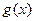на сегменте .

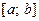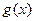
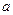
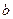
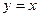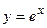Пример 3. Вычислить площадь плоской фигуры, ограниченной линиями и при 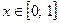(см. Рис. 7).

Если построить графики указанных линий (см. Пример 1 Лекция № 7), то роль функции 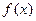играет функция 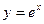, а в качестве функции 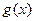выступает функция 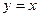, следовательно,

.

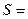
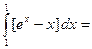
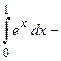
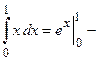
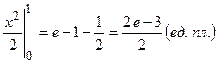5. Если непрерывная кривая, ограничывающая криволинейную трапецию, задана в параметрическом виде 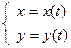при 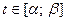, то площадь трапеции вычисляется по формуле .

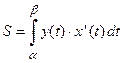Пример 4. Вычислить площадь под одной аркой циклоиды .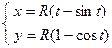

Циклоида – это кривая, которую описывает точка на ободе колеса при его полном повороте, следовательно, для одной арки циклоиды параметр 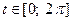. По приведенной формуле площадь под аркой циклоиды равна

.

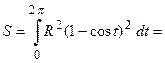
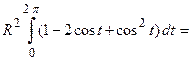
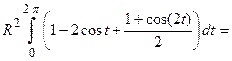
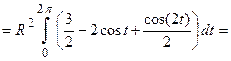
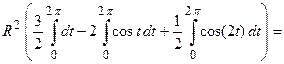
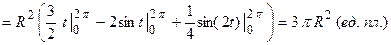6. Если непрерывная кривая, ограничывающая криволинейную трапецию, задана в полярной системе координат 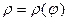и фигура ограничена лучам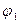и и 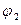, то площадь плоской фигуры вычисляется согласно формуле

.

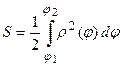Пример 5. Найти площадь плоской фигуры, ограниченной одним витком спирали Архимеда.

Спираль Архимеда (см. Лекцию № 9 Первый семестр) описывается уравнением 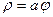. Для одного витка спирали Архимеда угол 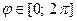. Используя вышеприведенную формулу, получаем

.

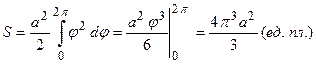2. Вычисление объема и площади поверхности тела.

1. (объем любого тела с известным законом изменения площади поперечного сечения) Пусть дано некоторое тело, для которого известен закон изменения площади поперечного сечения, например, вдоль оси абсцисс, т.е. 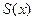(Рис. 11).

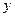
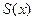Рис. 11. Объем тела с задан-

ным законом изменения пло-

щади поперечного сечения.

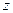
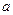
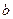
Тогда объем такого тела вычисляется по формуле .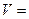

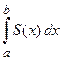Пример 6. Вычислить объем эллипсоида .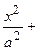

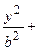
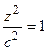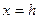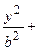
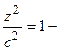
Если зафиксировать абсциссу, т.е. положить , то получим 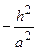. Разделив это равество на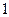 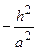, найдем, что в плоскости 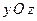эллипс описывается уравнением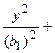 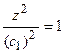с полуосями

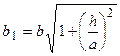и .

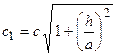Вычислим площадь этого эллипса (Рис. 12):

Рис. 12. Отыскание закона измене-

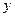ния площади поперечного сечния

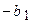
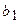эллипсоида.

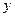
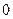
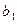
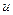
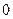
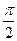
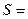
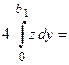
Так как эллипс симметричен относительно координатных осей, то достаточно вычислить площадь его четвертой части (см. Рис. 12) и увеличить полученную площадь в 4 раза, т.е. 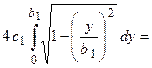(произведем замену переменной интегрирования)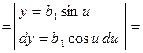(пересчитаем пределы интегрирования по формуле замены)

.

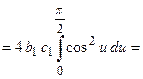
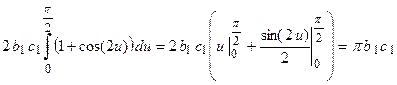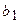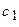Следовательно, площадь поперечного сечения в направлении оси абсцисс с учетом выражений для полуосей и определяется формулой

.

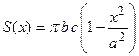Таким образом, объем эллипсоида будет равен

.

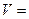
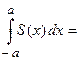
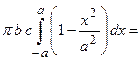
2. (объем тела вращения)

О1. Если тело получается путем ротации лини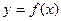и (или 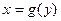) вокруг оси 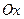(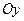), то оно называется телом вращения.

Площадь поперечного сечения такого тела описывается формуло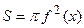й (или 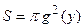), следовательно, объем тела вращения вычисляется по формуле: 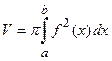– при вращении вокруг оси абсцисс;

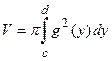– при вращении вокруг оси ординат.

Пример 7. Вычислить объем тела вращения, если оно получено путем ротации линии (Рис. 8) вокруг оси абсцисс при .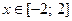

Согласно приведенной формуле

.

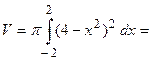
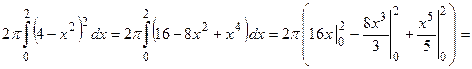
3. (площадь поверхности тела вращения) Площадь поверхности тела вращения вычисляется по формуле

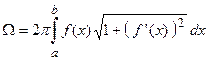– при вращении вокруг оси абсцисс;

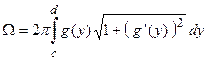– при вращении вокруг оси ординат.

Пример 8. Вычислить площадь поверхности тела вращения шара радиуса .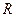

Шар получается путем вращения линии 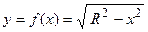вокруг оси абсцисс при 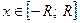. Первая производная от указанной функции

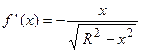, следовательно,

.

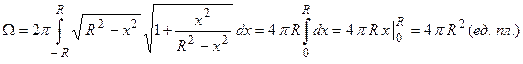3. Длина дуги.

1. Если линия определяется явной функцией 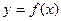, то длина дуги при 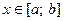вычисляется по формуле .

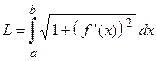2. Если линия задана параметрическ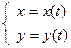и при 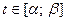, то длина дуги вычисляется по формуле .

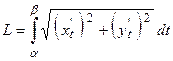3. Если линия задана в полярной системе координат 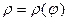и дуга ограничена лучам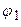и и 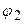, то то длина дуги вычисляется по формуле .

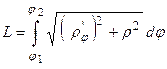Пример 9. Вычислить длину дуги 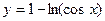при .

Вычислим первую производную от заданной функции 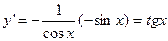. Таким образом, 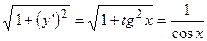. Следовательно, длина дуги

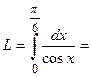
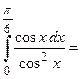
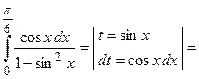(пересчитаем пределы интегри-

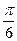
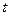
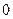
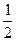
рования)

.

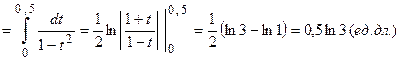Лекция № 10 “Несобственные интегралы”

1. Определенные интегралы с одним или двумя бесконечными пределами интегрирования от непрерывной на интервале интегрирования функции.

(Несобственные интегралы I рода).

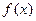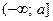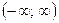Т1. Пусть функция непрерывна на интервале (или интервалах ; ). Если существует предел 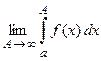(или пределы ;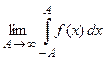, соответственно), то существует интеграл 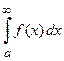(или интегралы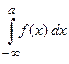;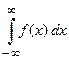, соответственно).

О1. Определенный интеграл с одним или двумя бесконечными пределамиинтегрирования от непрерывной на интервале интегрирования функции называется несобственным интегралом I рода

(;).

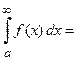
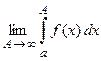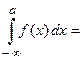
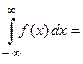
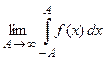З1. Несобственный интеграл I рода вычисляется в смысле главного значения.

В дальнейшем будем изучать только интегралы 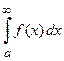, другие интегралы рассматриваются аналогично.

Пример 1. Вычислить интеграл .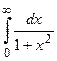

.

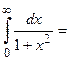
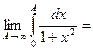
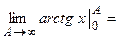
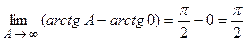Пример 2. Вычислить интеграл .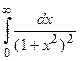

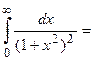
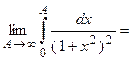(применим метод замены переменной интегрирования)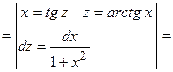(пересчитаем пределы интегрирования)

.

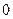
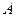
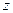
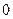
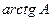
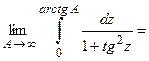
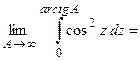
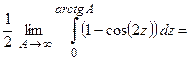
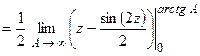
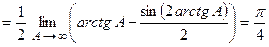О2. Несобственный интеграл I рода называется сходящимся, если пределы в указанных выше равенствах конечны, в противном случае несобственный интеграл I рода называется расходящимся.

Пример 3. Выяснить сходимость интеграла .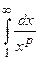

Рассмотрим возможные случаи:

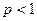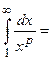
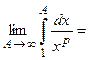
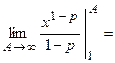
а) : 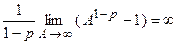– расходится;

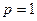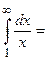
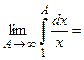
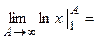
б) : 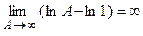– расходится;

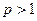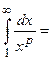
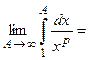
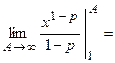
в):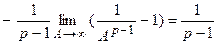– сходится.

Следовательно, данный несобственный интеграл расходится при 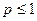и сходится при 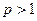. Этот интеграл часто используется в теории рядов (см. ниже).

Рассмотрим признак сходимости несобственного интеграла I рода:

Пример 4. Исследовать на сходимость интеграл .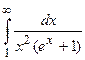

На интервале 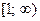справедливы неравенства 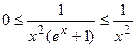. Так как 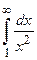(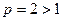) сходится (см. Пример 3), то по признаку сходимости сходится и интеграл .

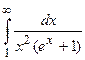Пример 5. Исследовать на сходимость интеграл .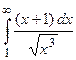

На интервале 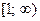справедливы неравенства 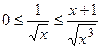. Так как 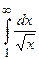(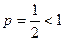) расходится (см. Пример 3), то по признаку сходимости расходится и интеграл .

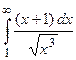Сл. из Т2. Если сходится интеграл 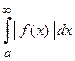, то сходится и интеграл .

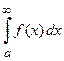Пример 6. Исследовать на сходимость интеграл .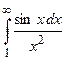

Так как 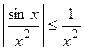и интеграл 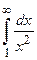(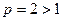) сходится (см. Пример 3.), то по признаку сходимости сходится и интеграл .

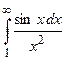2. Определенные интегралы с конечными пределами интегрирования от

функций, имеющих точки разрыва второго рода на интервале интегрирования.(Несобственные интегралы II рода).

О3. Если функция 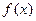не существует хотя бы в одной точке 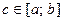, то интеграл 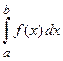называется несобственным интегралом II рода.

З2. Если функция 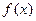в точке 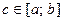терпит разрыв II рода, то обычное определение определенного интеграла как предела интегральной суммы непригодно.

Вычисление определенного интеграла с конечными пределами от разрывной на интервале интегрирования функции производится посредством предельного перехода ().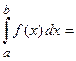

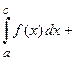
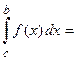
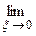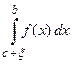О4. Если приведенные пределы существуют и конечны, то несобственный интеграл II рода называется сходящимся, в противном случае – расходящимся.

Пример 7. Вычислить интеграл .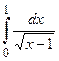

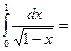
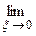
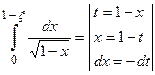(пересчитаем пределы интегрирования)

.

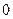
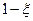
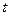
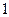
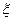
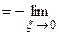
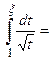
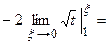
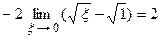Рассмотрим признак сходимости несобственных интегралов II рода:

Дата добавления: 2014-01-11