
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Логические функции и их преобразования
|
|
|
|
Формирование выражения для функции на основе таблицы истинности
Построение таблиц истинности для логических функций
Таблица истинности была определена в п.1. Определим её ещё раз.
Таблица истинности функции: таблица, устанавливающая соответствие между возможными наборами значений аргументов (логических переменных) и значениями функции.
Все столбцы таблицы истинности можно сгруппировать в 3 части. В первой части каждый столбец соответствует имени аргумента (логической переменной). Во второй части каждый столбец соответствует результату выполнения одной логической операции. Столбцы во второй части необходимо располагать «слева-направо» с учётом приоритета выполнения операций. Третья часть состоит из одного столбца – значений функции для различных комбинаций аргументов.
Количество строк в таблице истинности равно количеству комбинаций значений аргументов. Каждый аргумент имеет только 2 значения: 0 и 1. По этой причине количество m комбинаций значений аргументов для n аргументов равно m = 2n. Каждую комбинацию значений аргументов удобно представлять в виде числа в системе счисления с основанием р=2, начиная с 0 и кончая числом m-1. В таблице на Рис. Представлена таблица со всеми комбинациями значений для 3-х аргументов: a, b, c.
| Номер комбинации аргументов | Значения аргументов | ||
| a | b | c | |
Т.к. все логические функции представляют собой соединение логических переменных с помощью базовых операций (функций), необходимо, как и для арифметических операций, определить порядок выполнения логических операций, т.е. определить их приоритеты (старшинство).
|
|
|
| Операция | Отрицание ( ) )
| Конъюнкция (ab) | Дизъюнкция (a V b) | Импликация, Эквивалентность |
| Приоритет |
В этой таблице показано, что при записи без скобок последовательности логических операций, в первую очередь выполняются операции «отрицание», во вторую очередь – операции «логическое умножение», в третью – операции «логическое сложение» и в четвёртую очередь – операции «импликация» и «эквивалентность». Последние 2 операции имеют равный приоритет, и выполняются в порядке записи в выражении.
Для изменения естественного порядка выполнения логических операций используются круглые скобки.
Пример. Построить таблицу истинности для функции F(a,b)= ¬ (a \/ ¬b).
| a | b | ⌐b | a \/ ¬b | F(a,b)= ¬ (a \/ ¬b) |
Пример. Построить таблицу истинности для логической функции: F(a,b,c)=b↔(a+c).
| a | c | a+c | b | F(a,b,c)=b↔(a+c) |
В данной таблице истинности столбцы первой части разделены столбцом со значениями функции (a+c), имеющейся в выражении. Это сделано для удобства определения значений этой функции.
Алгебраическое выражение для логической функции можно построить по таблице истинности, применяя КНФ (конъюнктивную нормальную форму) или ДНФ (дизъюнктивную нормальную форму).
Формирование алгебраического выражения рассмотрим на примере таблицы истинности, представленной на Рис.
| a | b | c | F(a,b,c) |
|
|
|
Формирование выражения для логической функции на основе КНФ: в таблице истинности рассматривать только строки, которые соответствуют значению функции «0»; для каждой такой строки записать дизъюнкцию из элементов строки; каждый элемент «а», имеющий значение «0», записать в дизъюнкции как «а», каждый элемент «b», имеющий значение «1», инвертировать, т.е. записать как «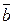 »; полученные дизъюнкции объединить конъюнкциями.
»; полученные дизъюнкции объединить конъюнкциями.
F1(a,b,c) = (a+b+c)(a+ 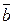 +c)(
+c)( +b+c)(
+b+c)( +b+
+b+  )
)
Формирование выражения для логической функции на основе ДНФ: в таблице истинности рассматривать только строки, которые соответствуют значению функции 1; для каждой такой строки записать конъюнкцию из элементов строки; каждый элемент «а», имеющий значение «1», записать в конъюнкции как «а», каждый элемент «b», имеющий значение «0», инвертировать, т.е. записать как «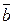 »;полученные конъюнкции объединить дизъюнкциями.
»;полученные конъюнкции объединить дизъюнкциями.
F2(a,b,c) =
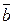 с +
с +  bc + ab
bc + ab  + abc
+ abc
Построим для каждой функции F1 и F2 таблицы истинности и покажем, что эти выражения равносильны, т.е. имеют одинаковые значения для одинаковых комбинаций значений аргументов.
Таблица истинности функции
F1(a,b,c) = (a+b+c)(a+ 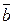 +c)( +c)( +b+c)( +b+c)( +b+ +b+  ) )
| ||||||||||
| a | b | c | 
| 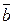
| 
| a+b+c | a+ 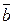 +c +c
|  +b+c +b+c
|  +b+ +b+ 
| F1(a,b,c) |
Таблица истинности функции F2(a,b,c) = 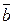 с + с +  bc + ab bc + ab  + abc + abc
| ||||||||||
| a | b | c | 
| 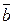
| 
|  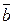 с с
|  bc bc
| ab 
| abc | F2(a,b,c) |
В алгебре логики установлены определённые стандартные преобразования, которые позволяют упрощать исходные логические выражения, и получать более простое выражение – результат, которое является равносильным исходному выражению.
|
|
|
Цель выполнения преобразований: привести исходное логическое выражение либо к КНФ, либо к ДНФ.
| Номер | Выражение | Название |
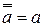
| Двойное отрицание | |
| ab = ba | Переместительный закон | |
| a+b = b+a | Переместительный закон | |
| a(bc) = (ab)c | Сочетательный закон | |
| a+(b+c) = (a+b)+c | Сочетательный закон | |
| a&a&a&…&a = a | ||
| a+a+a+…+a = a | ||
a& = 0 (a = 0 (a =0) =0)
| Закон противоречия: невозможно, чтобы противоречащие высказывания были одновременно истинными. | |
a+ = 1 = 1
| Закон исключённого третьего: либо высказывание, либо его отрицание должно быть истинным. | |
| a&1 = a | ||
| a+1 = 1 | ||
| a&0 = 0 | ||
| a+0 = a | ||
| (a+b)(c+d) = ac+ad+bc+bd | Раскрытие скобок | |
a → b =  +b +b
| Импликация (логическое следование) | |
a ↔ b = (a → b) (b → a) =
= ( +b)( +b)(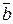 +a) = +a) =  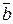 +ab +ab
| Эквивалентность (равнозначность) | |
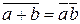
| Отрицание от дизъюнкции (закон де Моргана) | |
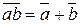
| Отрицание от конъюнкции (закон де Моргана) | |
| a(b+c) = ab+ac | Закон дистрибутивности | |
| a+bc = (a+b)(a+c) | Закон дистрибутивности | |
a+ b = a+b b = a+b
| Правило свёртки | |
 +ab = +ab =  +b +b
| Правило свёртки | |
ab + c + bc = ab + c + bc = ab + c c
| Правило сокращения (расширения) | |
abc + a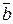 c = ac c = ac
| Правило склеивания |
Пример 1. Упростить выражения:
F1(a,b)=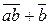 =
=  +
+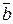 +
+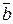 =
=  +
+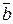
F2(a,b,c)=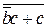 =
= 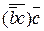 = (b+
= (b+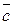 )
)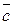 = b
= b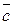 +
+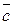 =
= 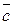 (b+1) =
(b+1) = 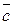
F3(a,b,c)=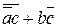 = (a+
= (a+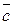 )+b
)+b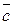 = a+
= a+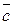 (1+b) = a+
(1+b) = a+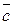
F4(a,b,c) = (a+b)c+abc(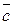 +ab)+
+ab)+ 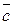 ab+
ab+ b
b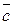 = ac+bc+abc
= ac+bc+abc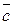 +abcab+b
+abcab+b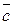 (a+
(a+ ) =
) =
= ac+bc+abc+b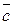 = ac(1+b)+b(c+
= ac(1+b)+b(c+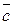 ) = ac+b
) = ac+b
Пример 2. Найти отрицание следующей импликации (логического следования): «Если урок будет интересным, то никто из учеников (Маша, Виктор, Светлана) не будет смотреть в окно».
Решение.
Обозначим высказывания:
i (interesting) – «Урок интересный»;
M – «Маша смотрит в окно»;
B – «Виктор смотрит в окно"»;
C – «Светлана смотрит в окно"».
Алгебраическое выражение для импликации:
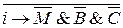 =
= 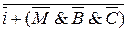 = i&
= i&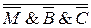 = i(M+B+C)
= i(M+B+C)
Словесное выражение отрицания импликации: «Урок интересный и либо Маша, либо Виктор, либо Светлана смотрит в окно».
Пример 3. Определить участника преступления, исходя из двух импликаций (логических следований):
|
|
|
1) «Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал»;
2) «Если Иванов не участвовал, то Сидоров не участвовал».
Решение.
Обозначим высказывания:
И – «Иванов участвовал в преступлении»;
П - "Петров участвовал в преступлении";
С- "Сидоров участвовал в преступлении".
Запишем сложное, состоящее из двух импликаций выражение в виде формулы:
F(И,П,С) = ((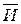 +П)→С)&(
+П)→С)&(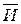 →
→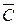 ) = (
) = (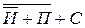 )&(
)&(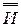 +
+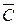 ) = (И
) = (И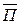 +С)(И+
+С)(И+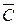 ) =
) =
= И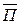 И+ И
И+ И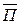
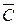 +ИС+С
+ИС+С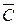 = И
= И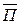 + И
+ И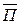
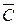 +ИС = И
+ИС = И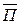 (1+
(1+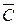 )+ИС = И
)+ИС = И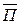 +ИС = И(
+ИС = И(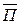 +С)
+С)
Для определения участника преступления это выражение должно иметь значение «истина»: И(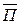 +С)=1. В полученной конъюнкции оба элемента должны иметь значение «истина». Определим, при каких значениях аргументов это выражение равно 1. И=1 (Иванов является участником преступления).
+С)=1. В полученной конъюнкции оба элемента должны иметь значение «истина». Определим, при каких значениях аргументов это выражение равно 1. И=1 (Иванов является участником преступления).
(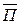 +С)=1
+С)=1
Составим таблицу истинности для этой функции и добавим к ней значение И=1:
| И | П | 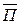
| С | 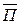 +С +С
| F (И,П,С) |
По условию задачи количество участников преступления – 1. В таблице истинности этому условию удовлетворяет строка №1. Т.е. преступление совершил Иванов.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1344; Нарушение авторских прав?; Мы поможем в написании вашей работы!