Приклади використання функцій Ляпунова

У даному розділі розглядаються приклади побудови функцій Ляпунова для конкретних динамічних систем. Дані приклади хоча і є формальними, однак вони дозволяють продемонструвати суть подібного аналізу при дослідженні конкретних економічних систем, для яких математичні моделі складаються із систем автономних диференційних рівнянь.

Приклад №1. Дослідити стійкість нульового розв’язку системи

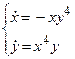
Розв’язок. Якщо взяти

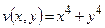, то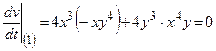

й, отже виконані умови теореми 1), тому нульовий розв’язок стійкий. До речі, у цій задачі проходить ще один прийом, що корисно взяти на озброєння, хоча спрацьовує він, на жаль, досить рідко: якщо у вихідній системі одне рівняння поділити на інше, тоді все зводиться до звичайного рівняння першого порядку, яке легко розв’язується.

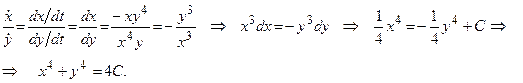
Отримані криві на фазовій площині є обмеженими, тому нульовий розв’язок стійкий. Те, що розв’язок вихідної системи виявилося можливим записати через функцію Ляпунова у вигляді 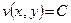не випадково. Якщо систему 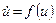вдається розв’язати аналітично, то результат зазвичай записується у вигляді (першого) інтегралу 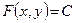, і при з'ясуванні питання про стійкість-нестійкість на роль функції Ляпунова треба у першу чергу спробувати взяти функцію 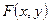. Втім, явний вид розв’язку системи допомагає для дослідження стійкості краще будь-яких непрямих методів.

Приклад №2. Дослідити стійкість нульового розв’язку системи

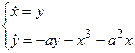
при всіх значеннях параметра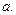

Розв’язок. Почнемо з використання теореми Ляпунова про перше наближення: будуємо матрицю Якобі для нашої системи та знаходимо її вид при 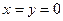( 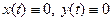- нульовий розв’язок системи, який треба дослідити на стійкість за Ляпуновим).

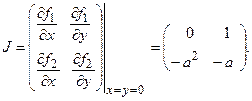
Знаходимо власні числа отриманої матриці:

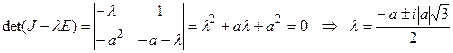
Таким чином, при нульовий розв’язок асимптотично стійкий (дійсна частина обох коренів від’ємна), при - нестійкий, при 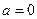нічого сказати не можна. Якби в правій частині системи були тільки лінійні доданки, то у випадку 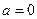була б стійкість, тому що 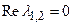, але не асимптотична стійкість. Але оскільки в правій частині присутні нелінійні доданки, то саме вони починають тепер впливати та вирішують характер стійкості.

Отже, досліджуємо окремо випадок 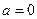. Система тоді приймає вид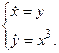

Як вже у розглянутому вище прикладі, її можна розв’язати та знайти перший інтеграл, поділивши друге рівняння на перше:

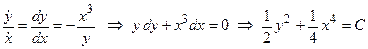
Фазові криві обмежені, тому 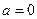відповідає стійкості нульового розв’язку. Якщо взяти 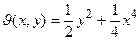, то її системна похідна буде тотожно дорівнює нулю, сама функція 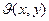дорівнює нулю у точці 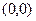, та додатна у всіх інших точках з околиці нуля, тому для доведення стійкості достатньо послатися на теорему (1).

Приклад №3. Дослідити стійкість нульового розв’язку системи

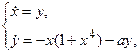
при всіх значеннях параметра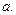

Розв’язок. Будуємо матрицю Якобі в нулі для застосування теореми Ляпунова про перше наближення:

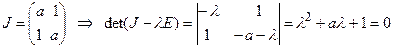
Корені цього рівняння, .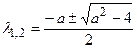

При 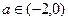точка (0,0) стійкий фокус,

при 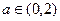точка (0,0) нестійкий фокус,

при 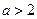точка (0,0) стійкий вузол,

при 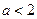точка (0,0) нестійкий вузол,

при а=2 точка (0,0) стійка зірка,

при а=-2 точка (0,0) нестійка зірка

необхідно окреме дослідження. Знову ділення одного рівняння системи на інше дозволяє знайти перший інтеграл:

.

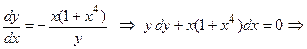
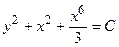І системна похідна тотожно дорівнює нулю.

Приклад 4. Дослідити стійкість нульового розв’язку системи

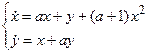
при всіх значеннях параметра a.

Застосуємо теорему Ляпунова про перше наближення:

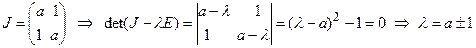
Якщо a < -1, то обидва корені від’ємні, значить нульовий розв’язок асимптотично стійкий. Якщо a > -1, то корінь l = a + 1 додатний, і нульовий розв’язок нестійкий. Випадок a = -1 необхідно розглянути окремо, оскільки права частина вихідної системи нелінійна. В цьому випадку одержуємо систему

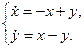
Для даного значення параметра нелінійна система стала лінійною, тому подальші дослідження не потрібні. Для лінійних систем l1 = 0 та l2 = -2 означають стійкість нульового розв’язку. Простий вид отриманої системи дозволяє довести стійкість нульового розв’язку іншими методами:

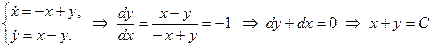
Явний зв'язок між x і y дозволяє досліджувати питання стійкості нульового розв’язку без спроб побудови функції Ляпунова, досить залежність y = C - x підставити в перше рівняння системи. Тоді

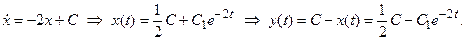
Експоненти при t ® ¥ прагнуть до нуля, тому нульовий розв’язок вихідної системи буде стійким, але не асимптотично стійким, тому що постійні доданки C не прагнуть до нуля.

Також тут можна довести стійкість за допомогою функції Ляпунова, взявши в її якості наступну функцію J(x, y) = x² + y² та використовуючи теорему 1.

Приклад 5. Дослідити стійкість нульового розв’язку системи

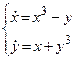
Спробуємо в якості функції Ляпунова взяти v(x, y) = ax² + by² з довільними параметрами a, b. Тоді

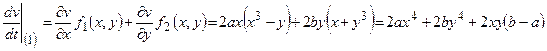
Якщо a = b = 1, то функція Ляпунова буде всюди, крім нульової точки x = y = 0, додатною також буде і її системна похідна. Тому, застосовуючи теорему 3), одержуємо нестійкість нульового розв’язку.

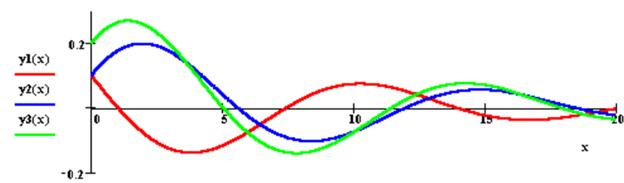
Пример 6. Изменение объема производства в некоторой замкнутой экономической системе описывает дифференциальное уравнение второго порядка

y'' +2|k|y' + w²y = 0.

В замкнутой экономической системе нет экспорта, импорта и притока капитала извне. Уравнение описывает поведение разности y(x)=Y(x)-G/s между объемом производства Y(x) и фиксированной величиной G/s отношения правительственных расходов к предельной склонности населения к сбережению.

Ниже приведены графики решений уравнения при k=0.25, w²=0.25 при различных начальных условиях. Видно, что колебания решений около нуля — периоды спада и подъема в экономике — зависят от начального состояния системы.

Дата добавления: 2014-01-11