Взаимосвязь между различными формами моделей объекта

Уравнения в переменных состояния объекта дают ряд преимуществ с точки зрения анализа и синтеза систем. Единообразие описания через дифференциальные уравнения первого порядка позволяет облегчить доказательства управляемости и наблюдаемости, по единой методике синтезировать регуляторы для объектов различного порядка, создавать единообразные алгоритмы для расчетов системы. Одним из основных преимуществ является, как будет показано позднее, получение при синтезе непосредственно алгоритмов для цифрового управления.

Важным моментом в описании объектов через координаты состояния является то, что набор этих координат может быть выбран различным. Например, модель четырехполюсника на рис. 3.3. может быть представлена через координаты состояния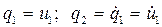

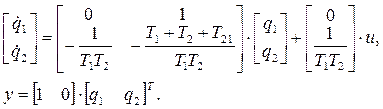(3.14)

Рис. 3.5 Структурная модель четырехполюсника в канонической

форме управляемости

На рис. 3.5. представлена структура системы (3.14). (сравните со структурной схемой рис. 3.4.). Не сложно доказать, что (3.10) и (3.14) дают одно и то же дифференциальное уравнение относительно входного u₁ и выходного напряжений

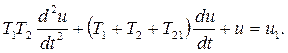(3.15)

Координаты моделей (3.10) и (3.14) связаны линейными зависимостями

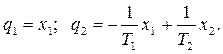
Как уже отмечалось, переменные х₁, х₂, … х_n образуют вектор Х =[ х₁,… х_n] пространства Rⁿ над полем вещественных чисел. Это пространство носит название пространства состояний объекта. Переменные q₁, q₂,… q_n так же образуют вектор Q =[q₁,… q_n ] того же самого пространства, но, очевидно, в другом координатном базисе (или в других координатах). Эти координатные базисы линейно связаны между собой, поэтому в общем случае можно записать

или в матричной форме

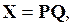(3.16)

где Р – преобразующая матрица.

Из (3.16) следует, что один и тот же объект мы можем описать в пространстве состояний относительно различных базисов (координат) этого пространства. Выбор того или иного базиса влияет на вид коэффициентных матриц в модели объекта.

Если в уравнении (3.7) сделать подстановку (3.16), то получим

Умножив левую и правую части уравнения на р^-1, получим:

(3.17)

Обозначив

получим уравнения в новом базисе:

Способы определения матриц перехода из одного координатного координатного базиса в другой изложены в Приложении 2.

Подобные преобразования применяются для получения коэффициентных матриц в форме удобной для анализа и синтеза систем. На первоначальном этапе описания объекта за координаты состояния стремятся принять физически измеряемые промежуточные перемене, как это было в рассматриваемых примерах с четырехполюсником и электродвигателем.

При этом, как правило, получаются коэффициентные матрицы произвольной формы.

Однако, для исследования объекта на управляемость, а также для синтеза регуляторов по полному вектору состояния объекта удобно представить модель в так называемой канонической форме управляемости или нормальной форме (см. Приложение 2).

(3.18)

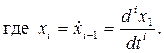
На рис. 3.6. представлена структурная схема модели в канонической форме управляемости. Очевидно, что система (3.14) и структура на рис. 3.5. являются представлением объекта второго порядка в нормальной форме. Для электродвигателя определена матрица преобразований модели относительно физических координат в модель нормальной формы. Кроме нормальной формы широко используется каноническая форма наблюдаемости, диагональная и др.

Если описание объекта задано моделью, связывающую вход-выход дифференциальным уравнением или передаточной функцией, то переход к модели, описывающей объект в пространстве состояний, наиболее просто осуществляется через нормальную форму (или каноническую форму управляемости).

Рис. 3.6 Структурная модель «n» мерного объекта

в канонической форме управляемости

В общем виде:

Несложно доказать, что связь между коэффициентами передаточной функции и коэффициентами матриц при описании в нормальной форме (3.14) определяется соотношениями

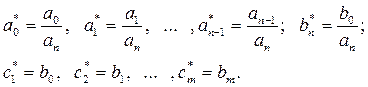(3.19)

Справедливость этих соотношений подтверждается рассмотренным выше примером.

При b_n=0 и a_n=1 выражения (3.19) значительно упрощаются.

Кроме того коэффициенты нижней строки матрицы перехода совпадают с коэффициентами характеристического уравнения системы.

Для получения модели двигателя в нормальной форме можно также воспользоваться передаточной функцией, которая легко получается из системы уравнений (3.11). (Момент нагрузки M_H принимаем равным нулю)

- электромагнитная и электромеханическая постоянные времени.

Переход от описания объекта в пространстве состояний к структурно-операторному в виде передаточной функции осуществляется очевидным способом путем исключения промежуточных переменных. Можно также получить передаточную функцию, подвергнув выражение (3.7) преобразованию Лапласа

(3.20)

Из первого уравнения (3.20) получим

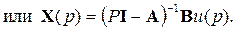
Подставим значение Х (р) во второе уравнение (3.20)

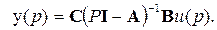
Следовательно

Применяя правило возведения матриц в отрицательную степень получим

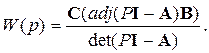(3.21)

Рассмотрим на примере четырехполюсника применение формулы (3.21). Из (3.14) следует

(3.23)

Окончательно числитель передаточной функции согласно (1.26) равен

Знаменатель равен определителю матрицы (1.27)

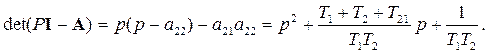
Делением числителя на знаменатель получаем

Это выражение совпадает с выражением (3.15) при замене .

Вывод передаточной функции двигателя по данной методике необходимо произвести самостоятельно.

Из (3.21) следует, что зная матрицу перехода можно определить корни характеристического уравнения, заменив р на l

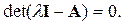(3.23)

Это делает возможным исследовать устойчивость системы по критерию Рауса-Гурвица, а заменив р на jw - по критерию Михайлова.

Для исследования реакции системы на внешние воздействия необходимо решить матричное дифференциальное уравнение (3.7). Рассмотрим первоначальное уравнение первого порядка (3.3.). Его решение определяется известным выражением

(3.24)

где х(0) – начальное значение x(t).

В частном случае при u(t)=const в интервале времени от 0 до t интеграл в (3.24) берется довольно легко

(3.25)

Решение матричного уравнения (3.7) имеет подобный вид [6]

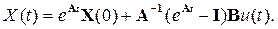(3.26)

Отличие (3.26) от (3.25) в его многомерности. Поэтому возникает задача определения экспоненциальной функции от матрицы. Для этого можно использовать два подхода. Первый состоит в разложении функции в степенной ряд

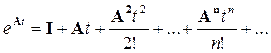(3.27)

Выражение (3.27) дает приближенное значение функции. Для точного аналитического расчета воспользуемся методом Кэли-Гамильтона. Любую функцию от матрицы можно представить в виде

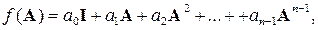(3.28)

где n – размерность квадратной матрицы A и коэффициенты а_i определяются из системы уравнений

(3.29)

i = 1,2,… n; l_i – собственные значения матрицы 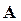(или корни уравнения (3.23)).

Аналитическое решение уравнения довольно громоздкая задача. Поэтому чаще используются машинные методы расчета. Для этого выражение (3.27) представим в следующем виде

(3.30)

Такое представление значительно упрощает алгоритм расчета.

Дата добавления: 2014-01-11