Полугруппа

Алгебра с одной бинарной ассоциативной операцией называется полугруппой. Бинарная операция называется ассоциативной, если (a * b)* c = a *(b * c). Часто, операцию в полугруппе называют произведением. В дальнейшем мы тоже будем придерживаться данного соглашения. Однако, следует помнить, что произведение в полугруппе не всегда коммутативная операция. Например, множество квадратных матриц порядка n с рациональными элементами относительно операции умножения матриц образуют полугруппу, и операция не коммутативна.

Свойство 2.1. Результат перемножения n элементов в полугруппе не зависит от способа расстановки скобок.

Доказательство проведем индукцией по числу сомножителей. При трех сомножителях утверждение очевидно. Пусть оно верно для любого числа сомножителей меньше n. Покажем его справедливость для n сомножителей. Выделим в произведении два элемента, умножаемых в последнюю очередь. Допустим .Рассмотрим два случая.

1. Пусть k =1. По предположению индукции в произведении 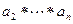скобки можно расставлять произвольным образом. Расставим их следующим способом . В результате все произведение представится в виде .

2. Пусть k =2,…, n -1. По предположению индукции в произведении 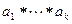скобки можно расставлять произвольным образом. Расставим их следующим способом 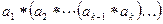. В результате все произведение представится в виде 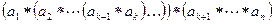равное в силу ассоциативности операции 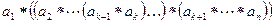. Последнее произведение рассмотрено в случае 1.

Таким образом, вне зависимости от расстановок скобок, результат равен , что и доказывает требуемое утверждение.

Элемент полугруппы 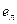называется левым нейтральным (или левой единицей), если для любого другого элемента полугруппы a справедливо равенство .

Аналогично вводится понятие правой единицы .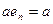

В полугруппе может существовать несколько левых (правых) единиц. Например, на множестве матриц вида любая матрица вида 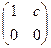является левой единицей. Правых единиц нет.

Свойство 2.2. Если в полугруппе есть левая и правая единица, то они равны.

Действительно, произведение по определению левой единицы равно правой единице, а по определению правой единицы равно левой единице. Следовательно, левая и правая единицы равны.

Полугруппа, в которой имеется левая и правая единица (которые в этом случае совпадают) называется полугруппой с единицей. Нейтральный элемент в этом случае обозначают через e (без индексов).

В полугруппе с единицей могут существовать решения уравнений ax = e и xa = e. Решение первого уравнения обозначается 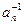и называется правым обратным элементом к a, а решение второго уравнения обозначается и называется левым обратным элементом к a.

Свойство 2.3. Если к элементу полугруппы a существуют левый и правый обратные элементы, то они равны.

Доказательство вытекает из равенства .

Если к элементу a существуют левый и правый обратные элементы, которые в этом случае совпадают, то тогда говорят об обратном элементе и обозначают его 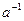(без индексов).

Дата добавления: 2014-01-11