Тема. Теория вероятностей

Определение. Теория вероятностей – это наука, изучающая закономерности в случайных явлениях.

Определение. Случайное явление – это такое явление, которое при неоднократном испытании протекает каждый раз по-разному.

Определение. Опыт – деятельность человека или процесс, испытания.

Определение. Событие – результат опыта.

Определение. Предметом теории вероятностей являются случайные явления и специфические закономерности массовых случайных явлений.

Классификация событий:

1. Событие называется достоверным, если в результате опыта оно обязательно произойдет.

Пример. Школьный урок обязательно закончится.

1. Событие называется невозможным, если при заданных условиях оно никогда не произойдет.

Пример. Если в цепи нет электрического тока, лампа не загорится.

1. Событие называется случайным или невозможным, если в результате опыта оно может произойти или не произойти.

Пример. Событие – сдать экзамен.

1. Событие называется равновозможным, если условия появления одинаковые и нет основания утверждать, что в результате опыта одно из них имеет шанс появиться больше, чем другое.

Пример. Выпадение герба или решки при броске монеты.

1. События называются совместными, если появление одного из них не исключает возможностей появления другого.

Пример. При выстреле, промах и перелет – события совместные.

1. Событие называется несовместным, если появление одного из них исключает возможность появления другого.

Пример. При одном выстреле попадание и промах – события не совместные.

1. Два несовместных события называются противоположными, если в результате опыта одно из них обязательно произойдет.

Пример. При сдаче экзамена, события «сдал экзамен» и «не сдал экзамен», называются противоположными.

Обозначение: 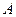- нормальное событие, 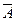- противоположное событие.

1. Несколько событий образуют полную группу несовместных событий, если в результате опыта наступит только одно из них.

Пример. При сдаче экзамена возможно: «не сдал экзамен», «сдал на «3»», «сдал на «4»», - полная группа несовместных событий.

Правила суммы и произведения.

Определение. Суммой двух произведений a и b называют событие c, которое состоит в появлении события a или события b или обоих одновременно.

Сумму событий называют объединением событий (появление хотя бы одного из событий).

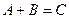
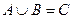
Если в задаче по смыслу очевидно, что должно появиться a ИЛИ b, то говорят, что находят сумму.

Определение. Произведением событий a и b называют событие c, которое состоит в одновременном появлении событий a и b.

Произведением называют пересечение двух событий.

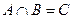
Если в задаче говорят, что находят a И b, значит находят произведение.

Пример. При двух выстрелах:

1. если необходимо найти попадание хотя бы один раз, то находят сумму.
2. если необходимо найти попадание два раза, то находят произведение.

Вероятность. Свойство вероятности.

Определение. Частотой некоторого события называют число равное отношению числа опытов, в котором событие появилось к числу всех произведенных опытов.

Обозначение: r(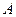) – частота события .

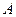Пример. Подбрасывая монету 15 раз, и при этом герб выпадет 10 раз, тогда частота появления герба: r()=.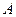

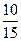Определение. При бесконечно большом количестве опытов, частота события становится равна вероятности события.

Определение классической вероятности. Вероятностью события 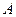называют отношение числа благоприятствующих появлению этого события случаев к числу всех единственно возможных и равновозможных случаев.

Обозначение: 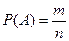, где P – вероятность,

m – число случаев благоприятствующих появлению события .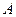

n – общее число единственно возможных и равновозможных случаев.

Пример. В соревнованиях по бегу принимают участие 60 студентов ЧИЭПа. Каждый имеет номер. Найти вероятность того, что номер студента, выигравшего забег не содержит цифры 5.

.

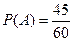Свойства вероятности:

1. значение вероятности не отрицательное и заключено между значениями 0 и 1.
2. вероятность равна 0, тогда и только тогда, когда это вероятность невозможного события.
3. вероятность равна 1, тогда и только тогда, когда это вероятность достоверного события.
4. вероятность одного и того же события неизменно, не зависит от количества проведенных опытов и меняется только тогда, когда изменятся условия проведения опыта.

Определение геометрической вероятности. Геометрической вероятностью называют отношение части области, попадание в которой выбранной точки необходимо найти во всей области, попадание в которой в данной точке равновозможно.

Область может быть мерой площади длины или объема.

.

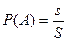Пример. Найти вероятность попадания некоторой точки на участок длиной 10 км, если необходимо, чтобы она попала вблизи концов отрезка, не далее, чем на 1 км от каждого.

.

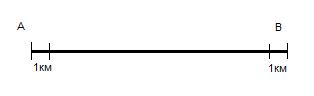
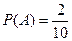Замечание.

Если меры области s и S имеют разные единицы измерения по условию задачи, то для решения необходимо s и S придать единую размерность.

Соединение. Элементы комбинаторики.

Определение. Объединения элементов различных групп, отличающиеся порядком элементов или хотя бы одним элементом называют соединениями.

Соединения бывают:

- размещение

- сочетание

- перестановки

Определение. Размещениями из n – элементов по m раз, называют соединение, отличающееся друг от друга, хотя бы одним элементом и порядком расположения элементов.

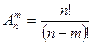
Определение. Сочетаниями из n элементов по m, называется соединение, состоящее из одних и тех же элементов, отличающиеся хотя бы одним элементом.

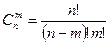
Определение. Перестановками из n элементов, называют соединения, состоящие из одних и тех же элементов, отличающееся друг от друга только порядком расположения элементов.

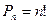
Пример.

1) сколькими способами можно составить автоколонну из 5 автомобилей.

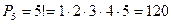
2) сколькими способами можно назначить в классе 3х дежурных, если всего человек в классе 25.

Так как порядок элементов не важен и группы соединений отличаются количеством элементов, то вычислим число сочетаний из 25 элементов по 3.

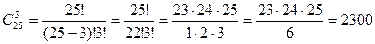способов.

3) Сколькими способами из цифр 1,2,3,4,5,6 можно составить 4х значное число. Следовательно, т.к. соединения отличаются порядком расположения и хотя бы одним элементом, то вычислим размещение из 6 элементов по 4.

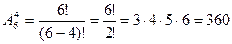
Пример на использование элементов комбинаторики, на вычисление вероятности.

В партии из n изделий – m – бракованных. Произвольным образом выбираем l-изделий. Найти вероятность того, что среди них окажется ровно k – браков.

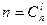
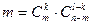
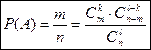
Пример.

В магазин на склад привезли 10 холодильников из них 4- 3хкамерных, остальные – 2хкамерные.

Найти вероятность того, что среди выбранных произвольным образом 5 холмов – 3 будут 3хкамекрными.

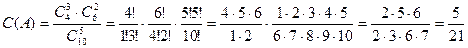
Основные теоремы теории вероятностей.

Теорема 1.

Вероятность суммы 2х несовместных событий равна сумме вероятностей этих событий.

Следствие.

1) если событие образует полную группу несовместных событий, то сумма их вероятностей равна 1.

2) сумма вероятностей 2х противоположных событий равна 1.

Теорема 2.

Вероятность произведения 2х независимых событий равна произведению их вероятностей.

Определение. Событие A называется независимым от события В, если вероятность появления события А не зависит от того произойдет событие В или нет.

Определение. 2 события называются независимыми, если вероятность наступления одного из них зависит от появления или не появления второго.

Определение. Вероятность события В вычисленное при условии, что событие А имело место, называют условной вероятностью.

Теорема 3.

Вероятность произведения 2х независимых событий равна вероятности появления одного события на условную вероятность второго при том, что первое событие произошло.

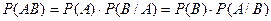
Пример.

В библиотеке имеется 12 учебников по математике. Из них, 2 учебника по элементарной математике, 5 – по теории вероятностей, остальные – по высшей математике. Выбираем произвольным образом 2 учебника. Найти вероятность того, что они оба поп элементарной математике.

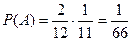
Теорема 4. Вероятность появления события хотя бы 1 раз.

Вероятность появления хотя бы одного из событий, образующих полную группу несовместных событий равно разности между первым и произведением вероятностей противоположных данным событий.

Пусть 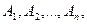тогда

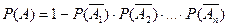
Следствие.

Если вероятность появления каждого из события 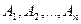, одинакова и равна p, тогда вероятность того, что появится хотя бы одно из данных событий, равно

, где

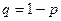, n – количество произведенных опытов.

Пример.

Производят 3 выстрела по мишени. Вероятность попадания при первом выстреле 0,7, при втором – 0,8, при третьем – 0,9. найти вероятность того, что при трех независимых выстрелах в мишень будет:

А) 0 попаданий;

Б) 1 попадание;

В) 2 попадания;

Г) 3 попадания;

Д) хотя бы одно попадание.

а) P(A)=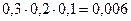

б)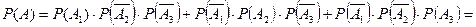

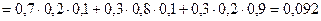
в)

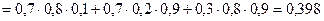
г)

д) .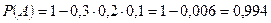

Теорема 5. Формула полной вероятности.

Пусть событие А может появиться совместно с одной из гипотез 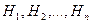, тогда вероятность того, что событие А произошло, находят по формуле:

.

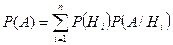Гипотезы 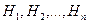- образуют полную группу несовместных событий и суммы вероятностей гипотез равна 1.

.

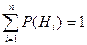Пример.

Среди поступающих на склад магазина 1000 изделий:

300 шт. – изделие 1 фабрики

500 шт. – изделие 2 фабрики

200 шт. – изделие 3 фабрики.

Вероятность появления браков: 1 фабрики – 0,01

2 фабрики – 0,02

3 фабрики – 0,03.

Найти вероятность того, что купленное в данном магазине изделие окажется бракованным.

Событие А – купили бракованное изделие.

Событие А может появиться совместно с одной из трех гипотез:

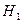- изделие 1 фабрики

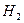- изделие 2 фабрики

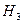- изделие 3 фабрики.

.

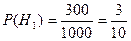
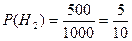
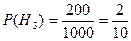
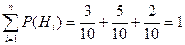
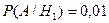
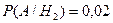
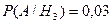
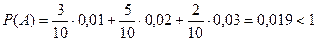Теорема 6. Теорема Байеса (теорема гипотез).

Пусть событие А может появиться совместно с одной из гипотез 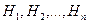, если известно, что событие А произошло, то вероятность того, что оно произошло совместно с i – гипотезой, находят по формуле:

.

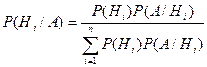Пример.

В условиях предыдущей задачи найти вероятность того, что известно – куплено бракованное изделие. Какова вероятность того, что это изделие 1 фабрики.

.

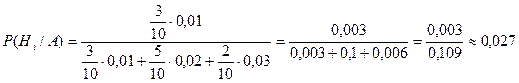Теорема 7. Формула Бернулли.

Пусть производится n – независимых испытаний, в каждом из которых событие А может появиться m раз.

Вероятность появления события А, в каждом из опытов равно p. Тогда вероятность того, что событие А появится указанное число раз, находят по формуле:

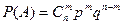, где

.

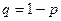Пример.

Что вероятнее выиграть у равносильного противника: 1 партию из 2х или 2 партии из 4х.

Вычислим отдельно вероятности выигрышей 1й партии из 2х и 2х партий из 4х.

.

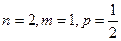В каждом опыте вероятность выигрыша 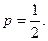Следовательно, .

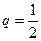1) вероятность выигрыша 1 партии из 2х.

.

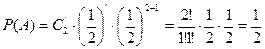Вычислим вероятность выигрыша 2х партий из 4х.

n=4, m=2.

.

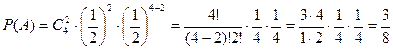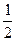и 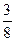. Приводим к общему знаменателю.

.

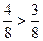Т.о. выиграть одну партию из 2х у равносильного противника вероятнее, чем выиграть 2 партии из 4х.

Дата добавления: 2014-01-11