Устойчивость САР. Методы исследования и критерии

АНАЛИЗ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ САР

Устойчивость динамических систем – это их свойство возвращаться в прежнее (невозмущенное) состояние после окончания действия возмущений. Таким прежним состоянием может быть, например, состояние покоя (положение равновесия), или какой-то известный, установившийся, закон изменения управляемой переменной y (t), описывающий некоторый режим функционирования (движения) САР. На математическом языке ему будет соответствовать определенное частное решение y* (t) уравнений динамики системы.

Невозмущенное движение y *(t) будет асимптотически устойчивым, если после окончания действия возмущений, отклонение от него стремится к нулю:

D y (t) = | y (t)– y *(t)| ® 0 при t ®¥.

В зависимости от величины начального отклонения D₀=D(t ₀) различают следующие виды асимптотической устойчивости невозмущенного движения:

а) в малом (D₀ бесконечно мало); б) в большом (D₀ ограничено по величине); в) в целом (D₀ может быть любым).

Устойчивой называют систему, в которой любое невозмущенное движение устойчиво. Для такой системы устойчивость будет «внутренним» свойством, а не особенностью какого-либо режима ее работы или вида движения.

Для нелинейной системы устойчивость какого-то конкретного невозмущенного движения не гарантирует устойчивости других невозмущенных движений. Кроме того, из устойчивости движений в малом, в общем случае, не следует их устойчивость в большом или в целом.

Для линейных систем устойчивость какого-либо одного, даже тривиального, невозмущенного движения гарантирует устойчивость всех других (любых) невозмущенных движений, а, следовательно, и устойчивость самой системы. Более того, из устойчивости линейной системы в малом, следует ее устойчивость и в большом, и в целом.

В общем случае, отклонение D y (t) при t ³0 вызвано действием внешних сигналов и ненулевыми начальными условиями. Соответственно этому различают возмущения сигнальные и возмущения по начальным условиям.

Полную реакцию любой (даже нелинейной) системы всегда можно представить как сумму невозмущенного движения y *(t) и отклонения от него D y (t):

y (t) = y *(t)+D y (t).

Для линейных систем выполняется принцип суперпозиции и возмущенное движение всегда можно представить в виде суммы некоторого частного решения y _частн(t) неоднородного уравнения (с правой частью) и общего решения соответствующего однородного (без правой части) уравнения системы:

y (t) = y _общ(t) + y _частн(t).

При этом общее решение имеет вид , где p_i – характеристические корни ЛДС (случай простых, некратных корней). Если частное решение отыскивается в форме вынуждающей функции входа u (t), то его называют вынужденной (стационарной, установившейся) составляющей y _частн(t)= y _в(t) выходного сигнала. Тогда другую часть полного решения называют переходной составляющей y _общ(t) = y _п(t) и при этом

y (t) = y _п(t) + y _в(t).

Переходная составляющая процесса y _п(t) в общем случае также имеет две компоненты: y _п(t) = y _а(t) + y _сс(t). Здесь y _а(t) - та часть переходного процесса, которая определяется начальными условиями и не зависит от входа. Она описывает процесс в автономной (без внешних воздействий) системе. Компонента y _сс(t) – часть переходного процесса, не зависящая от начальных условий, но зависящая от вида входного сигнала. Это собственная сопровождающая для y _в(t).

Тогда y (t) = y _п(t) + y _в(t) = y _а(t) + y _сс(t) + y _в(t)= y _а(t) + y ₀(t), где y ₀(t) – это реакция системы на внешнее воздействие при нулевых начальных условиях.

Таким образом, полное движение ЛДС можно представить суммой (суперпозицией) двух составляющих: первая – движение за счет начальных условий при нулевом входе (движение автономной системы), а вторая – движение системы за счет внешнего воздействия при нулевых начальных условиях: y (t)= y _а(t) + y ₀(t). В классической теории линейных САУ рассматриваются и изучаются только процессы при нулевых начальных условиях.

Если y_п(t)®0 при t ®∞, то ЛДС называется устойчивой (асимптотически). В противном случае ЛДС либо неустойчива (y _п(t) возрастает по величине), либо находится на границе устойчивости. При этом может быть два вида границы устойчивости: а) колебательная, когда y _п(t) имеет вид гармонических колебаний и б) апериодическая, когда y _п(t)=const.

Для выяснения математических условий устойчивости линейных систем, описываемых уравнением «вход – выход» вида A (D) y (t) =B (D) u (t), рассмотрим выражение для переходной составляющей процесса

,

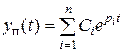где p_i – корни характеристического полинома A (p) = A (D) при D=p.

В таком виде формула для y _п(t) справедлива, когда все характеристические корни различны. В случае кратного корня p_i, соответствующий ему коэффициент C_i в формуле будет полиномиальной функцией времени (степень полинома меньше коэффициента кратности корня на единицу).

В общем случае эти корни могут быть и вещественными (p_i= α _i) и кóмплексными (p_i,i+1= α _i ± j b _i), а общее их число (с учетом кратности) равно порядку характеристического полинома n. При этом парциальная составляющая переходного процесса, соответствующая вещественному корню p_i имеет вид. Она затухает асимптотически во времени только в том случае, когда p_i= α _i < 0. Для пары комплекно-сопряженных корней p_i,i+1 соответствующая им парциальная составляющая имеет следующий вид:

,

где | C_i |=| C_i+1 |=Mod C_i, j _i =-j _i+1 =arg C_i.

Эта составляющая будет затухать только при a _i = Re p_i < 0 («левые» корни). Если хотя бы для одного корня a _i >0 («правый» корень), то соответствующая ему парциальная составляющая процесса со временем будет увеличивать свои значения и ЛДС будет неустойчивой. При отсутствии правых корней, но при наличии пары сопряженных корней на мнимой оси (p_i,i+1= ± j b _i), ЛДС будет находиться на колебательной границе устойчивости. Если один корень нулевой (p_i = 0), а остальные – «левые», то ЛДС находится на апериодической границе устойчивости.

Таким образом, для устойчивости ЛДС необходимо и достаточно, чтобы все корни характеристического уравнения A (p)=0 были «левыми», т.е. имели отрицательные вещественные части. При этом условие устойчивости ЛДС (y _п(t)® 0) не будет зависеть от величины начальных условий, внешних возмущений и вида вынужденной составляющей, а определяется только расположением характеристических корней системы на комплексной плоскости.

Если окажется устойчивым хотя бы одно, например тривиальное, движение ЛДС, то устойчивым будет и любое другое невозмущенное движение, т.к. в при этом y (t) ® y _в(t). Следовательно, устойчивость ЛДС – это ее «внутреннее» свойство, а не свойство конкретного режима или вида ее движения.

В соответствии с этим, для линейной системы можно дать несколько э квивалентных определений свойства устойчивости. ЛДС устойчива, если:

1) все характеристические корни лежат в левой полуплоскости: p_i ÎЛПП;

2) свободная (переходная) составляющая процессов y _п(t) затухает;

3) полная реакция стремится к вынужденной составляющей: y (t) ® y _в(t);

4) весовая функция w (t) затухает, т.е. стремится к нулю (более строго – является абсолютно интегрируемой функцией);

5) переходная функция h (t) стремится к некоторому постоянному значению.

Для неустойчивой линейной системы свободная (переходная) составляющая процесса y _п(t) не затухает, а неограниченно нарастает. Такая система, очевидно, не может обеспечить изменение управляемой переменной по заданному извне закону. Следовательно, устойчивость САУ является необходимым условием ее работоспособности. В то же время САУ, построенная только из функционально необходимых звеньев, может оказаться неустойчивой. Поэтому анализ устойчивости и ее обеспечение (стабилизация) являются важнейшими задачами ТАУ.

Если САУ можно стабилизировать только изменением параметров без изменения ее структуры, то она структурно устойчива. Для такой системы в пространстве параметров существует не пустая область, внутренним точкам которой соответствуют устойчивое расположение всех характеристических корней. Множество таких точек образует область устойчивости ЛДС.

Для стабилизации структурно-неустойчивой системы в ее состав включают дополнительные (корректирующие) звенья. Как правило, с их помощью не только стабилизируют систему, но и меняют характер поведения свободной составляющей и обеспечивают близкий к желаемому закон изменения вынужденной составляющей y _в(t).

Методы исследования устойчивости ЛДС можно разделить на прямые и критериальные. Прямые методы связаны с нахождением характеристических корней или решений уравнений динамики САУ с последующей проверкой одного из условий устойчивости. В настоящее время, при современном уровне развития вычислительных средств и компьютерных технологий, эта группа методов становится все более популярной при исследовании САР повышенной сложности. Недостаток их в том, что получаемое компьютерное решение имеет частный характер и из него неясно, как изменять параметры системы (или структуру) для ее стабилизации или повышения запасов устойчивости. Кроме того, для систем с высоким порядком математической модели, при решении уравнений могут возникать и вычислительные проблемы.

Критериальные методы исследования устойчивости не требуют решения уравнений, а основываются на проверке некоторых условий и правил для коэффициентов ММ ЛДС, либо для ее частотных свойств и характеристик. Такие математические условия и правила называют критериями устойчивости. Соответственно этому различают алгебраические (аналитические) и частотные (графоаналитические) критерии устойчивости.

Критерии устойчивости могут быть а) необходимые; б) достаточные и в) необходимые и достаточные.

Требования необходимого критерия выполняются для любой устойчивой системы, а их нарушение гарантирует, что ЛДС не является устойчивой (она либо неустойчива, либо на границе устойчивости). Однако выполнение требований этого критерия не позволяет определенно судить об устойчивости системы.

Выполнение требований достаточного критерия гарантирует устойчивость ЛДС, но их нарушение не позволяет судить об устойчивости или неустойчивости.

С помощью необходимого и достаточного критерия можно судить как об устойчивости, так и о неустойчивости ЛДС.

В основу алгебраических методов исследования устойчивости ЛДС положены следующие алгебраические критерии:

а) необходимый критерий устойчивости (критерий Стодолы);

б) критерий Рауса (1877);

в) критерий Гурвица (1895);

г) критерий Льенара – Шипара (1914);

д) критерий Зубова.

Исходными данными для применения критериев а) – г) являются коэффициенты характеристического полинома (многочлена) ЛДС, поэтому соответствующие им методы можно назвать коэффициентными.

Критерий Зубова в качестве исходных данных использует матрицу A в уравнениях состояния ЛДС, поэтому он относится к группе матричных критериев.

Основой частотных методов исследования устойчивости ЛДС являются следующие частотные критерии устойчивости:

а) критерий Михайлова; б) критерий Найквиста.

Критерий Михайлова базируется на исследовании частотных свойств характеристического полинома ЛДС, а критерий Найквиста – на анализе частотных характеристик разомкнутой системы с ЕООС. Известны также обобщения этого критерия для линейных САУ с произвольной структурой.

Все реальные системы являются нелинейными, а их линеаризация чаще всего осуществляется путем отбрасывания малых слагаемых, содержащих нелинейности (метод касательных). При этом возникает вопрос о возможности суждения об устойчивости (или неустойчивости) реальной системы по результатам исследования линеаризованной системы. Русским математиком А.М. Ляпуновым (1892 г.) были строго обоснованы следующие результаты:

· Если линеаризованная система устойчива, то невозмущенное движение реальной системы будет также асимптотически устойчивым (в малом);

· Если линеаризованная система неустойчива, то невозмущенное движение реальной системы также не будет асимптотически устойчивым;

· Если линеаризованная система на границе устойчивости (критический случай, когда есть корни на мнимой оси), то реальная система может оказаться как устойчивой, так и неустойчивой (из-за влияния отброшенных нелинейных слагаемых).

Дата добавления: 2014-01-11