Теорема Коши-Гельмгольца

Рис.4.5

В момент времени t в движущейся жидкости выделим в т. o (xj) жидкий элементарный объем в виде куба с ребрами δxj, которые в этот момент времени параллельны осям координат. Скорость жидкости в т. o пусть будет ui. За малый интервал времени D t вершина куба o переместится в т. o¢ (xj +D xj).

Проследим, что произойдет с жидкой частицей при ее перемещении. Для наглядности рассмотрим нижнюю куба грань с ребрами δx ₁ и δ x ₂, параллельную плоскости x₁x₂ (Рис.4.5). Компоненты скорости жидкости в т.т. a и c, удаленных от т. o на расстояния δx ₁ и δx ₂, соответственно равны:

; ; ; .

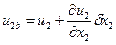Приращение 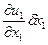показывает, насколько компонента u ₁ в точке a больше, чем в точке o. Следовательно, величину 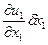можно представлять скоростью удлинения ребра oa, а - скоростью относительного удлинения ребра, т.е. скоростью удлинения (сжатия), отнесенной к его первоначальной длине. Величина 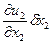представляет скорость удлинения ребра ob, а - скорость относительного удлинения (сжатия) ребра ob. Приращение является линейной скоростью вращения т. a вокруг оси, проходящей через т. o. Следовательно, будет угловой скоростью ребра oa в плоскости x ₁ x ₂. Аналогично, величина будет линейной скоростью вращения т. с относительно т. o, а угловой скоростью вращения ребра oс. Удлинение (укорочение) ребер вызывает, очевидно, линейную деформацию грани. Вращение ребер в общем случае приводит как к угловой деформации грани, так и к вращению грани как твердого тела. Совершенно очевидно, что рассуждения относительно деформации и вращения других граней жидкой частицы аналогичны. Выделим в чистом виде деформацию и вращение.

Принято скорость деформации жидкой частицы представлять величиной

.

При i=j величина скорости деформации представляет собой скорость объемной деформации жидкой частицы с компонентами e ₁₁ – скоростью линейной деформации растяжения (сжатия) в направлении x ₁, e ₂₂ – скоростью линейной деформации растяжения (сжатия) в направлении x ₂, e ₃₃ – скоростью линейной деформации растяжения (сжатия) в направлении x ₃. Если же i¹j, то величина e_ij является скоростью угловой деформации жидкой частицы.

Вращение жидкой частицы как твердого тела принято определять завихренностью

.

Здесь e_ijk – тензор перестановок, равный 1, если значения индексов изменяются по часовой стрелке, равный -1, если значения индексов изменяются против часовой стрелки и равен 0 при одинаковых значениях любых двух индексов. Компоненты вектора завихренности или вектора угловой скорости раны:

.

Вращательное движение частицы характеризуют еще и вихрем скорости: .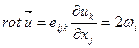

Отметим, что вихрь скорости (или завихренность) определяется тремя компонентами, т.е. является вектором, а величина - девятью компонентами, т.е. является тензором, и называется тензором скоростей деформации.

Скорость жидкости в малой окрестности точки x_j может быть представлена выражением:

или .

Это выражение означает, что скорость движения любой точки жидкой частицы в общем случае складывается из скорости поступательного, деформационного (линейного и углового) движения и скорости вращательного движения. В этом и состоит теорема Коши - Гельмгольца.

Течение, в котором отсутствует вращательное движение жидких частиц, называется незавихренным или безвихревым. Условием незавихренности течения является равенство нулю вихря скорости , а вернее .

4.12. Уравнение Навье – Стокса.

Чтобы было можно пользоваться уравнениями движения (4.13) или (4.14), необходимо уметь вычислять вязкие напряжения t_ij. Для их вычислений принято пользоваться гипотезой Стокса (1845г.): напряжения в жидкости пропорциональны соответствующим скоростям деформаций:

.

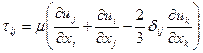Здесь d_ij – символ Кронекера, равный 1 при i=j и равный нулю, при i¹j. Смысл записи в такой форме состоит в том, что при i=j выражение в скобках равно нулю как для сжимаемой, так и для несжимаемой жидкости, в чем можно убедиться, пользуясь правилом суммирования по повторяющемуся индексу (в этом случае, вероятно, ).

Подставляя выражение для вязких напряжений t_ij в уравнение движения (3.14) получим уравнение Навье – Стокса:

. (4.32)

В уравнении n = m/r и m - кинематический и динамическй коэффициенты вязкости соответственно, - скорость объемной деформации, дивергенция вектора скорости.

Для установившегося течения несжимаемой жидкости уравнение Навье – Стокса имеет такой вид:

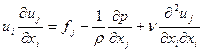. (4.33)

Хотя уравнение Навье – Стокса справедливо только для ламинарного течения (вязкость m имеет молекулярную природу), оно настолько сложны для использования в инженерной практике, что при расчете вязких течений используют различные упрощения реального течения.

Наиболее часто используемой моделью течения вязкой жидкости с относительно большими скоростями и малой вязкостью является течение с пограничным слоем.

Согласно этой модели поток в поперечном сечении делится на две части: тонкая пристенная область, в которой проявляется вязкость (пограничный слой), и невязкая часть потока – ядро течения.

Из-за того, что пограничный слой тонок, он обладает следующими свойствами:

1. давление поперек пограничного слоя не изменяется и равно давлению в соответствующей точке внешней границы пограничного слоя, т.е. ¶p/¶n =0;

2. продольный градиент давления в пограничном слое равен продольному градиенту давления во внешнем потоке (ядре течения);

3. 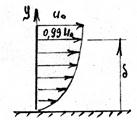в пограничном слое скорость изменяется из-за вязкости от нуля на стенке, до скорости на внешней границе пограничного слоя. За толщину пограничного слоя принимается расстояние d от стенки, на котором значение скорости отличается от скорости на внешней

Рис.4.6 границе на 1% (рис.4.6).

Гипотеза о пограничном слое не только дает возможность упростить решение уравнений Навье – Стокса, но и позволяет подойти к решению задачи о течении вязкой жидкости в пограничном слое другими методами. То, что влияние вязкости сказывается лишь вблизи обтекаемой поверхности, было отмечено еще Д.И.Менделеевым в 1880 году. Математический анализ задачи и вывод уравнений пограничного слоя принадлежит Л. Прандтлю (1904 г.). Рассмотрим упрощение уравнений Навье – Стокса, проведенное Прандтлем. Будем рассматривать установившееся движение несжимаемой жидкости в отсутствии массовых сил.

Поперек пограничного слоя скорость изменяется от нуля на стенке до скорости внешнего потока u ₀ на малом расстоянии d. Изменение скорости вдоль потока, т.е. вдоль координаты x значительно медленнее, чем по координате y. Тогда можно считать, что в пограничном слое справедливы оценки:

~ <<~; ~<<~.

Здесь l – длина обтекаемой поверхности, y – поперечная координата. Производные оцениваем по порядку изменения соответствующих величин на заданной характерной длине l. Поэтому в уравнении (4.32) можно отбросить первое слагаемое в последнем члене, что приведет к уравнению Л.Прандтля для ламинарного пограничного слоя:

,

где v – вертикальная компонента скорости. Это уравнение необходимо решать с уравнением неразрывности.

Контрольные вопросы и упражнения

1. Получить уравнение (4.30).

2. Почему работа вязких напряжений всегда положительна, необратима?

3. Что такое диссипативная функция?

4. Почему исчезла квадратная скобка в уравнении (4.31)?

5. Выскажите предположение, почему работа массовых сил не изменяет внутренней энергии жидкости.

6. Работа каких сил приводит к изменению внутренней энергии жидкости?

7. Какова причина угловой деформации жидкой частицы?

8. Какова причина вращения жидкой частицы?

9. Какова причина линейной деформации жидкой частицы?

10. Нужна ли теорема Коши-Гельмгольца для получения уравнений Навье Стокса?

11. В чем суть гипотезы Стокса?

12. Для какого режима течения выведены уравнения Навье-Стокса?

13. В чем заключается суть модели течения с пограничным слоем?

14. При каких условиях справедлива модель течения с пограничным слоем?

15. Каковы свойства пограничного слоя?

Дата добавления: 2014-01-11