Представление о центральной предельной теореме

Рассмотрим последовательность с.в. (n = 1,2,…). Под центральной предельной теоремой понимается теорема, устанавливающая условия, при которых сумма случайных величин Y_n при n ®¥ стремится к случайной величине, распределенной по нормальному закону.

Ниже приведем нестрогую формулировку центральной предельной теоремы Ляпунова.

Теорема Ляпунова. Пусть последовательность с.в. { X_n } (n =1,2,…) удовлетворяет следующим условиям:

1) " n независимы;

2) " i X_i имеет конечные математическое ожидание и дисперсию;

3) выполняется условие Ляпунова.

Тогда функция распределения с.в. при n ®¥ стремится к функции нормального распределения с м.о. 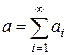и дисперсией .

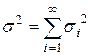Точное условие Ляпунова приводить не будем (его можно посмотреть в [Кремер]). Его содержательный смысл состоит в том, что вклад каждого слагаемого X_i в сумму Y_n при больших n ничтожно мал. Эта теорема объясняет тот факт, что в природе часто встречаются нормально распределенные с.в. Так, естественные размеры (рост человека, высота дерева) имеют нормальное распределение. Например, на высоту дерева влияют множество независимых факторов, каждый из которых существенно не влияет на общее действие всех факторов.

Лекция 7

Введение в математическую статистику

7.1 Основные понятия математической статистики

Часто исследователю приходится обрабатывать большие массивы данных, полученных в результате эксперимента путем измерений, наблюдений, анализа проб и т.п. Обычно экспериментатор имеет возможность многократно повторить свой опыт и получить большое количество однородных данных. Затем перед исследователем встает задача обработки этих данных, чтобы извлечь как можно более точную информацию об измеряемой величине. Изучением методов решения таких задач, в частности, занимается математическая статистика. Таким образом, в общих чертах математическая статистика разрабатывает математические методы, позволяющие делать существенные выводы об изучаемом объекте на основе статистических данных.

В теории вероятностей считаются известными законы распределения изучаемых случайных величин и на их основе изучаются другие свойства случайных величин. В математической статистике сама с.в. считается неизвестной, и целью исследования является получение более или менее достоверной информации об этом распределении на основе данных, собранных в результате наблюдений.

Более точно о некоторых задачах математической статистики скажем ниже после введения основных понятий.

Генеральной совокупностью (сокращенно г.с.) называется случайная величина, над которой происходит наблюдение.

Пусть X – г.с. Выборкой из г.с. X называется конечная последовательность независимых с.в.

, (7.1)

распределенных, так же как и X. Число n называется объемом выборки.

Если в результате опыта случайные величины выборки (7.1) получили числовые значения 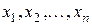соответственно, то последние называются реализацией выборки или выборочными значениями.

Рассмотрим пример. Имеется большая партия однотипных электрических лампочек. Требуется установить время безотказной работы лампы (время от включения и до перегорания лампы). Г.с. является с.в. X – время безотказной работы лампочек из этой партии. Можно выбрать наугад 10 лампочек из этой партии и измерить время безотказной работы каждой из выбранных лампочек: 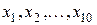. Эти числовые значения являются реализацией выборки объема 10. В принципе можно многократно провести измерения, каждый раз, выбирая по 10 лампочек. При этом каждый раз значения x_i будут различными. Поэтому результатом таких измерений следует считать цепочку независимых с.в. (7.1), т. е выборку объема 10. Итак, выборкой объема 10 является цепочка независимых случайных величин, каждая из которых является временем безотказной работы лампочек из этой партии. Номинальным (средним) значением времени безотказной работы лампы из партии является математическое ожидание г.с. M [ X ].

Теперь рассмотрим подробнее некоторые задачи математической статистики.

1. Оценивание параметров. Эта задача состоит в том, чтобы по реализации выборки найти приближенные значения характеристик г.с., таких, как параметры, входящие в закон распределения г.с., математическое ожидание и дисперсию г.с. т.п.

2. Проверка статистических гипотез. Бывает, что по реализации выборки из г.с. можно выдвинуть гипотезу о неизвестных параметрах или о функции распределения этой г.с. Задача состоит в том, чтобы разработать методы проверки (принятия или отвержения) таких гипотез.

3. Регрессионный анализ. Имеется результаты наблюдения над двумя случайными величинами. Требуется по ним установить, существует ли статистическая связь между ними. Если связь существует, то установить вид этой связи.

7.2 Точечные оценки неизвестных параметров г. с.

У г.с. неизвестными могут быть параметры, связанные с законом ее распределения, ее числовые характеристики (математическое ожидание, дисперсия и т.п.). Например, если предположить, что г.с. X имеет показательное распределение, то неизвестным может быть параметр l. В примере с электрическими лампочками неизвестным параметром является номинальное значение времени безотказной работы лампы из партии, т.е. математическое ожидание г.с. M [ X ].

Под оцениванием неизвестного параметра понимается нахождение его приближенного значения или диапазона его изменения. В первом случае оценка называется точечной, во втором – интервальной.

Пусть имеется выборка (7.1). Обозначим q неизвестный параметр г.с. X. С татистикой называется функция, зависящая от выборки (7.1). Например, 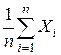, X ₁, – статистики. Очевидно, статистика является с.в. Если вместо выборки в статистику подставить реализацию выборки, то получится число, которое можно назвать реализацией статистики.

Точечной оценкой неизвестного параметра q г.с. X называется некоторая статистика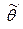, реализация которой считается приближенным значением параметра q.

Заметим, что статистики часто будут обозначаться буквой с волной над ней.

Свойства точечных оценок. Понятно, что точечная оценка неизвестного параметра должна обладать некоторыми «хорошими» свойствами по отношению к оцениваемому параметру. Рассмотрим эти свойства.

1. Несмещенность. Точечная оценка 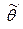неизвестного параметра q называется несмещенной, если , в противном случае оценка называется смещенной. Смысл несмещенности оценки состоит в том, что при нахождении приближенного значения неизвестного параметра по несмещенной оценке отсутствуют систематические ошибки (разность между значением оценки и оцениваемым параметром не имеет одного и того же знака).

2. Состоятельность. Точечная оценка 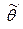неизвестного параметра q называется состоятельной, если =0 " e >0. Смысл состоятельности оценки состоит в том, что при увеличении объема выборки значение оценки будет приближаться к оцениваемому параметру.

3. Эффективность. Точечная оценка 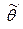неизвестного параметра q называется эффективной, если она имеет наименьшую дисперсию среди всех несмещенных оценок этого параметра. Смысл эффективности оценки состоит в том, что у эффективной оценки наименьшая ошибка оценивания параметра.

О методах получения точечных оценок. Есть различные способы получения точечных оценок. О трех из них о методе моментов, методе максимального правдоподобия и методе наименьших квадратов можно посмотреть в [ ].

Выборочной средней г.с. X называется статистика .

Выборочным начальным моментом k-го порядка называется величина

.

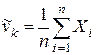Выборочным центральным моментом k-го порядка называется величина

.

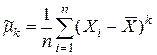Метод моментов состоит в том, что точечная оценка получается при замене неизвестных моментов г.с. (их еще называют теоретическими моментами) на соответствующие выборочные моменты. Так, точечной оценкой м.о. по этому методу является выборочное среднее, а точечной оценкой дисперсии – выборочный центральный момент второго порядка. Этот момент называется выборочной дисперсией и обозначается 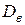или .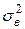

7.3 Точечные оценки математического ожидания и дисперсии. По всем перечисленным выше методам в качестве оценки математического ожидания M [ X ] получается выборочное среднее , а в качестве оценки дисперсии D (X) – выборочная дисперсия 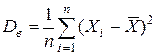. Кроме того, в качестве оценки дисперсии чаще рассматривают так называемую исправленную выборочную дисперсию 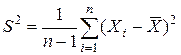. В качестве оценки среднеквадратического отклонения рассматриваются либо 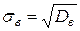, либо .

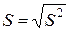Обозначим m = M [ X ] и 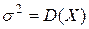. Выведем несколько полезных равенств.

1. .

Действительно, .

2. .

В самом деле, .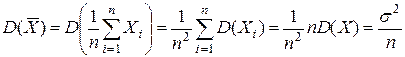

3. 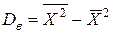, где .

Докажем это. =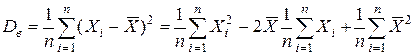

=.

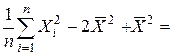
4. .

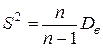Рассмотрим свойства введенных оценок. Свойство 1 означает, что выборочное среднее является несмещенной оценкой для м.о.

По закону больших чисел выборочное среднее является состоятельной оценкой для м.о.

Выборочное среднее не всегда является эффективной оценкой для м.о. Так, если г.с. распределена по нормальному закону, то эта оценка эффективна, но для равномерно распределенной г.с. это не так.

Докажем, что выборочная дисперсия 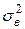является смещенной оценкой для дисперсии. Сначала преобразуем

=

=

=.

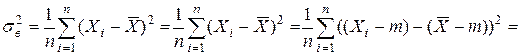
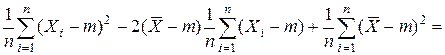
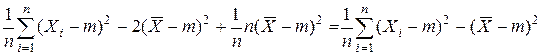Теперь вычислим м.о. от выборочной дисперсии:

=

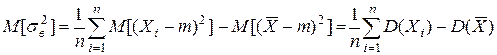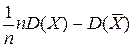==(по свойству 2)=.

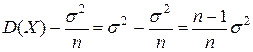Таким образом, Математическое ожидание от выборочной дисперсии «чуть» меньше дисперсии.

Исправленная выборочная дисперсия 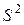является несмещенной оценкой для дисперсии. Действительно, по свойству 4 имеем

.

Наконец без доказательств приведем несколько фактов.

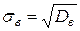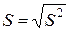1) и являются смещенными, но состоятельными оценками для среднеквадратического отклонения s.

2) D_в и 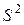являются состоятельными оценками для дисперсии.

3) Перечисленные в предыдущих пунктах 1) и 2) оценки не являются эффективными, но при больших объемах выборки они становятся почти эффективными.

7.4 Интервальные оценки. Основной недостаток точечной оценки состоит в том, что по нему нельзя сказать, насколько точно найдено приближенное значение неизвестного параметра. Интервальная оценка указывает промежуток, в который с некоторой вероятностью может попасть неизвестный параметр.

Пусть q – неизвестный параметр г.с. X, g – значение вероятности (т.е. 0< g <1), 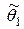и – статистики, не зависящие от параметра q. Интервал (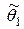, ) называется доверительным интервалом для параметра q с доверительной вероятностью (или надежностью) g, если выполняется равенство

.

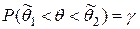Величина a =1– g называется уровнем значимости. На практике доверительные вероятности обычно выбирают равными 0.90, 0.95, 0.99. Смысл доверительного интервала состоит в том, что если провести большую серию опытов с одним и тем же объемом выборки, то примерно в 100 g % опытах доверительный интервал будет содержать неизвестный параметр.

Рассмотрим три закона распределения, которые часто используются в теории вероятностей.

1. Распределение 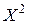(читается “хи в квадрате”). Пусть 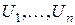ÎN(0, 1) – независимые нормально распределенные с.в. С.в. 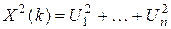называется распределенной по закону 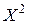со степенью свободы k.

2. Распределение Стьюдента Т (k). С.в. , где U ÎN(0, 1), называется распределенной по закону Стьюдента со степенью свободы k.

3. С.в. 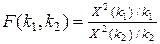, где k ₁, k ₂ – натуральные числа, называется распределенной по закону Фишера со степенями свободы k ₁, k ₂.

Рисунок 7.1

В математической статистике важную роль играет понятие квантили, введенное в лекции 4. Квантилью порядка a (0< a <1) называется такое число x _a, что

F (x _a) = a. В случае непрерывно распределенной с.в. с плотностью распределения p (x) F (x _a) = P (X < x _a) = . Это значит, что квантиль x _a – точка на оси х, в которой вертикаль отсекает слева от себя на графике плотности распределения криволинейную трапецию с площадью a (см. рис. 7.1). Если плотность распределения четная функция, т.е. ее график симметричен относительно оси у, то

x _a= – x _{1– a} (рис. 7.1). Квантили введенных выше распределений можно найти в таблицах в учебниках по теории вероятностей и математической статистике [ ].

Дата добавления: 2014-01-11