Предельная дискретизация во времени непрерывных сообщений с ограниченным спектром

В теории дискретизации непрерывных сообщении особую важность приобретает вопрос о максимальном интервале 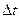=max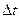, при котором возможно восстановление с заданной точности по ее отчетам.

Необходимое число отчетов при этом минимальна min m=[T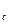/max].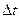

Дискретизация, соответственно такому берется целая часть условия – предельная (оптимальная). При этом обеспечивается представление непрерывного сообщения с заданной точностью минимального количества отчетов.

Проблема представления дискретизации сложна и несмотря на значительное количество исследовании далека до завершения.

В настоящее время наиболее разработанной и широко применяемой предельной дискретизацией непрерывных сообщений является дискретизация, основанная на теореме Котельникова.

Остановимся на исходных положениях этой теоремы. При построении теории дискретизации необходимо опираться на некоторую модель сообщения. Допустим, что известна одна из реализаций x(t) квазисто случайного процесса {x(t)}, соответственно совокупности возможных непрерывных сообщений.

Как бы сложна не была реализация, она представляет собой некоторую неслучайную (детерминируемую) функцию времени. На основе преобразовании Фурье – комплексный спектр

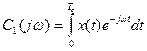(12)

Исходя из требуемой точности допустимого уровня помех, ограничим этот спектр некоторой частотой 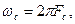т.е. введем модель сообщения с ограниченным амплитудным спектром. Особенность модели:

1. Относится к одной реализации случайного процесса, соответствует детерминированной

функции;

2. Имеет ограниченный спектр.

Для такой модели верна теорема: если непрерывная функция времени x(t) имеет спектр, ограниченный полосой частот от до , то эта функция полностью определяется последовательностью своих мгновенных значений, взятых в моменты времени, отсчитываемые через интервалы (теорема Котельникова).

Доказательств теоремы. Покажем, что x(t), заданная на интервале и не содержит составляющих с частотой выше 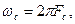(2) вполне определяется значениями 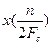функции в точках отсчета (а=1,2…) распределенных на расстояние друг от друга

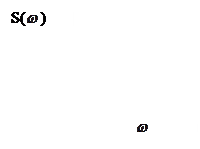
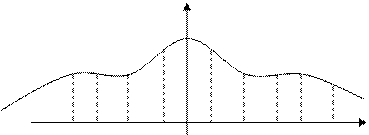
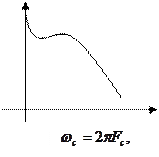
По условию теоремы S()=0 при 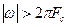. На интервале (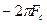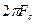) S() можно разложить как периодическую функцию с периодом 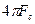в ряд Фурье

где (1)

(2)

Тогда для S():

(3) или , где (4)

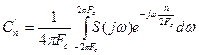(5)

С другой стороны по обратному преобразованию Фурье

(6)

с учетом S()=0 при

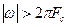
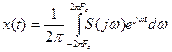(7)

Определим x(t) для дискретных моментов времени 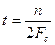, где .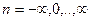

Для этого в (7) подставим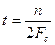

(8)

Сравнивая (8) с (5) видим, что коэффициенты 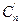разложения S() в пропорциональны отсчетом x(t) в дискретные моменты времени 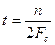, т.е.

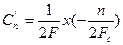(9)

Это выражение доказывает теорему.

Действительно, если функция времени x(t) известна в точках отсчета...,-, -, 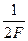то 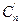определены.

Эти коэффициенты определяют S(), а S()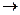x(t). Это означает, что существует единственная функция не содержащая частот выше и проходящая через заданные мгновенные значения в точках отсчета, отстающих друг от друга на интервал .

Связь между x(t) и S() определяем подставив (9) в (3):

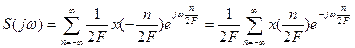
Так между x(t) и S() однозначная связь, то x(t) как и S() однозначно определяются отсчетом {}.

Т.О методика доказательства сводится:

1.Спектральная функция S() представляется рядом Фурье с коэффициентом 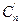(3)-(5)

2. По обратному преобразованию Фурье определяется функция времени в точках

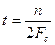(8)

3.Сравнивая (5) и (8) получаем связь коэффициентов Фурье 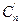с отчетами функции

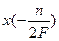, что доказывает теорему.

Дата добавления: 2014-01-13