Формула Тейлора. Задача аппроксимации (приближенного вычисления) функции в окрестности данной точки, которую часто называют рабочей точкой

Задача аппроксимации (приближенного вычисления) функции в окрестности данной точки, которую часто называют рабочей точкой, является одной из основных задач математического анализа. Для дифференцируемых функций эта задача решается с помощью формулы Тейлора.

Поскольку функция дифференцируема, то ее приращение представимо в виде:

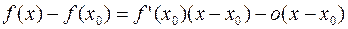
или

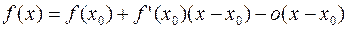
т.е. существует многочлен первой степени 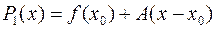, такой, что при 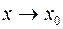выполняются условия , .

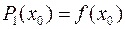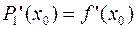В более общем виде задачу можно сформулировать следующим образом. Пусть функция определена в некоторой окрестности точки 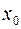и имеет в этой точке производных 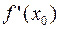, , 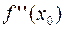…, 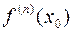. Необходимо найти многочлен 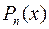степени не выше , такой, что

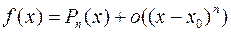
где 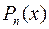удовлетворяет условиям:

;

;

;

;

.

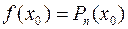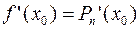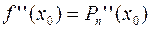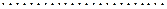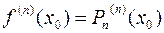Предположим, что искомый аппроксимационный многочлен имеет вид:

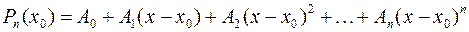
Тогда

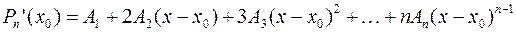
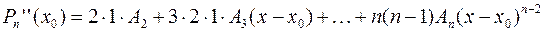
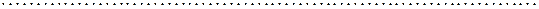
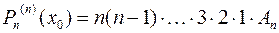
Тогда, с учетом условий (5), можно получить:

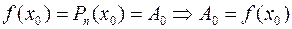
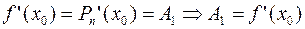
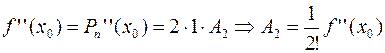
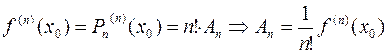
Таким образом, если в аппроксимационный полином подставить полученные значения коэффициентов, то полином можно записать следующим образом:

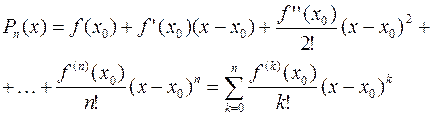
Этот многочлен называется многочленом Тейлора функции 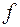. Можно показать, что он удовлетворяет условию 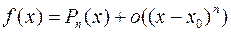. Рассмотрим функцию 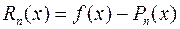. Эта функция представляет собой погрешность при замене функции 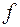многочленом 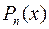в окрестности точки 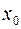. Из приведенных выше условий следует, что

.

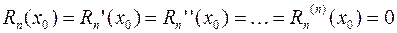Для того, чтобы убедиться, что 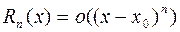при 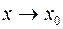необходимо показать, что 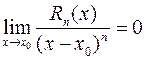. Для раскрытия этой неопределенности нужно применить раз правило Лопиталя:

Полученные выводы можно сформулировать в виде теоремы.

Теорема. Пусть функция 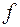определена в некоторой окрестности точк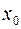и и раз дифференцируема в ней. Тогда при 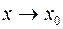имеет место формула:

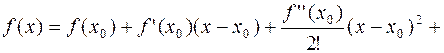
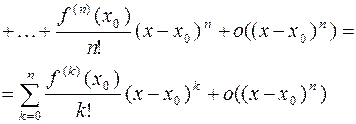
Полученный многочлен называется формулой Тейлора -го порядка с остаточным членом в форме Пеано.

Если 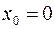, то формула Тейлора называется формулой Маклорена и имеет вид:

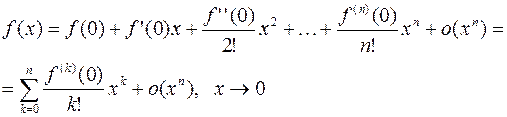
Для остаточного члена формулы Тейлора существуют и другие представления. Так, если функция 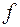имеет производную –го порядка в окрестности точки 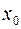, то остаточный член может быть представлен в форме Лагранжа:

, .

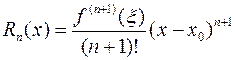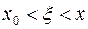Дата добавления: 2014-01-13