Окончательно в матричной форме

.

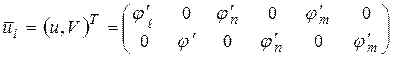Условия 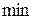функционалов (2¢) или (3) дают условия для определения значений степени свободы q_i с учетом :

=

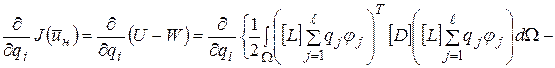
(9)

При решении системы полагается, что 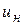удовлетворяет главным

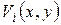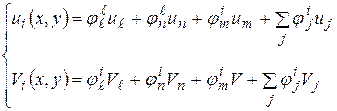граничным условиям . Здесь следует отметить, что выражения (7.2) и (7.3) для можно было записать в виде

, где ,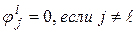

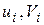то есть каждая определены для всей области, но они равны нулю в узлах кроме 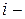го KЭ.

Ш. Получение из отдельных координатных функций элементов кусочно-непрерывной функции для всей области

При определении функций для КЭ по (4) или (5) искомая функция для всей области W определяется в виде:

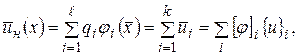
, (10)

где 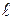- общее число степеней свободы (в общем случае не равно числу узлов, т.е. в каждый узел может быть введено различное число степеней свободы), 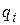- степени свободы в МКЭ, которые предоставляют искомые значения функции и их производных в узлах расчетной схемы (обычно). В (х) считают, что удовлетворяются главные граничные условия. Требования к и а) - линейно независимы; - положительны в энергетическом пространстве оператора А; их удовлетворение граничным условиям, дифференцируемость. В нашем случае 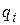есть .

IV. Составление разрешающей системы уравнений

путем минимизации функционала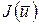

Для определения значений степени свободы 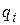с учетом (10) или имеем систему уравнений (9), где - называется матрицей жесткости.

Компоненты (элементы) матрицы и 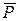- вектора для всей системы могут быть составлены из отдельных компонент. При этом принимается во внимание тот факт, что потенциальная энергия деформаций 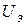и работа внешних сил W могут быть представлены в виде сумм по отдельным КЭ:

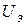=, W=.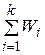

Этот факт позволяет строить матрицу жесткости и вектора

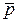Для всей системы из отдельных компонент. Например, - элемент матрицы и - ый элемент вектораопределяются по следующим формулам:

(12.1)

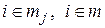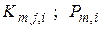где - означают суммирование по всем элементам, содержащим степени свободы; - компоненты матрицы жесткости и вектора узловых сил 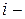го КЭ или

- вектор столбец,

(12.2)

Таким образом, элементы матриц накладываются друг на друга при формировании .

Компоненты (12.1) или (12.2) получаются из (9) с учетом (11) и выделения -го слагаемого из выражения энергии деформации, а также -го слагаемого из выражения для работы внешних сил для 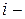го КЭ:

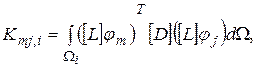
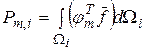(13)

Таким образом, МКЭ дает возможность строить разрешающую систему (9) 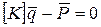на основе рассмотрения каждого К. Любая матрицаявляется квадратной. Каждая строка матрицы жесткости соответствует узлу и содержит кроме неизвестных значений в данном узле и неизвестные других узлов элементов, примыкающих к данному узлу. - размерности, где х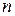², где N – число узлов; 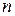- число неизвестных

(степеней свободы) в узлах.

V. Решение полученной разрешающей системы уравнений

Итак, имеется система 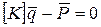. (14)

Причем, известные значения неизвестных, которые непосредственно задаются граничными значениями (условиями), могут быть исключены из системы (14). Можно поступить и иначе, приняв диагональный элемент матрицы жесткости (соответствующий узлу с известными по граничным условиям неизвестных) равным какой-либо большей величине, намного превышающей значения других элементов.

Полученная система может быть решена методом Гаусса. Но, поскольку она разреженная, то целесообразно применение итерационных методов (Зейделя, последовательной версии релаксации), Халесского.

VI. Вычисление искомых величин в элементах

После определения из (14) значений неизвестных функций для всех узлов, а далее по ним и, зная аппроксимации в КЭ, можно по обычным уравнениям связи определить другие величины, связанные с определенной величиной. Например, получив значения переменной с помощью обычных уравнений теорем упругости (соотношения Коши и закон Гука) определить распределения напряжений и деформаций.

Дата добавления: 2014-01-13