Ряды с положительными членами

Л е м м а. Ряд с положительными членами 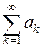сходится тогда и только тогда, когда все его частные суммы ограничены.

Доказательство следует из того факта, что частные суммы рядов с положительными членами 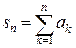монотонно возрастают с ростом 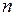, и значит, имеют предел тогда и только тогда, когда они ограничены сверху.

Теорема сравнения 1. Пусть 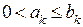. Тогда из сходимости ряда 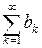следует сходимость ряда 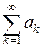и из расходимости ряда 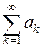следует расходимость ряда .

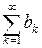Доказательство. Обозначая 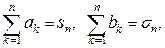имеем: 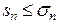. Остальное следует из доказанной леммы.

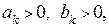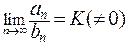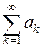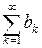Теорема сравнения 2. Пусть причем существует . Тогда ряды и сходятся или расходятся одновременно.

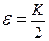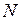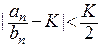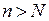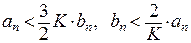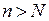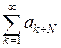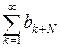Доказательство. Из определения предела при найдем такое, что при любом . Следовательно, при . Согласно теореме сравнения 1 ряды и сходятся или расходятся одновременно. Согласно свойству 2 сходящихся рядов теорема

доказана.

П р и м е р. Числовой ряд 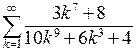сходится, так как его можно сравнить со сходящимся рядом 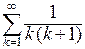, рассмотренным выше. Действительно, существует 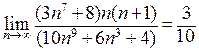, и можно применить теорему сравнения 2.

Два следующих достаточных условия сходимости числовых рядов с

положительными членами, называются признаками сходимости.

Признак Даламбера. Пусть существует 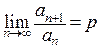. Если 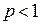, то ряд 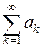сходится, если 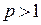, то этот ряд расходится.

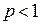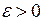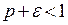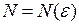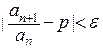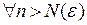Доказательство. 1) Пусть . Выберем такое, что и найдем номер такой, что для . Это значит, что 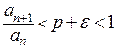для . Следовательно,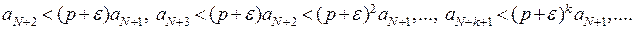

Это значит, что знакоположительный ряд сходится по теореме сравнения 1, так как сходится ряд 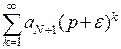(сумма бесконечной геометрической прогрессии со знаменателем 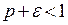). Согласно второму свойству числовых рядов исходный ряд также сходится.

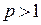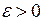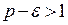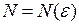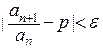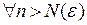2) Пусть . Выберем такое, что и найдем номер такой, что для . Это значит, что 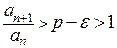для . Следовательно,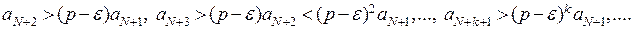

Это значит, что знакоположительный ряд расходится по теореме сравнения 1, так как расходится ряд 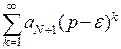(сумма бесконечной геометрической прогрессии со знаменателем 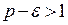). Согласно второму свойству числовых рядов исходный ряд также расходится.

П р и м е р. Исследуем сходимость ряда 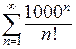. Здесь 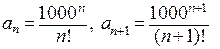. Так как 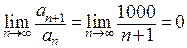, данный ряд сходится.

Признак Коши. Пусть существует 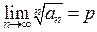. Если 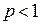, то ряд 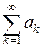сходится, если 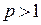, то этот ряд расходится.

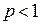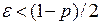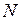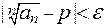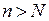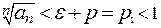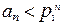Доказательство. 1)Пусть . Возьмем и найдем такое, что при . Следовательно, и при 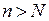. Согласно теореме сравнения 1 ряд 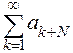сходится, так как сходится ряд 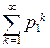. Следовательно, и исходный ряд сходится.

2) Пусть 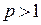. Возьмем 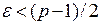и найдем 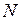такое, что

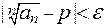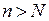при . Следовательно, 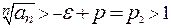и

при 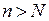. Согласно теореме сравнения 1 ряд 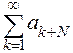расходится, так как расходится ряд 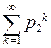. Следовательно, и исходный ряд расходится.

П р и м е р. Исследуем сходимость ряда 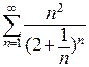. Так как 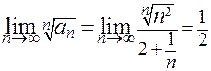, данный ряд сходится.

Следующий признак основан на сравнении ряда и несобственного интеграла, подынтегральная функция которого при натуральных значениях аргумента превращается в члены ряда.

Интегральный признак. Пусть члены ряда 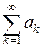монотонно убывают с ростом 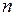. Если монотонная функция 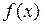такова, что 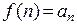, то сходимость или расходимость ряда 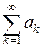равносильна сходимости или расходимости несобственного интеграла .

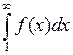Доказательство. Сравним частные суммы ряда с интегралом от функции 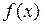по соответствующему отрезку. Для этого рассмотрим график функции 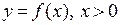, и отметим натуральные значения переменной и значения функции при этих натуральных значениях переменной.

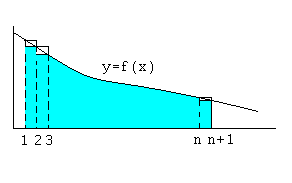
Закрашенная часть рисунка представляет собой область с площадью, равной

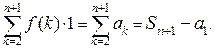
Закрасим теперь рисунок по-другому:

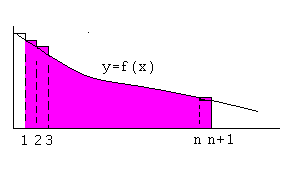
Теперь закрашенная часть рисунка представляет собой область с площадью, равной

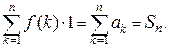
Легко заметить, что благодаря монотонности функции 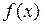справедливо неравенство: 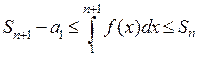. Следовательно, если несобственный интеграл 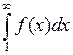сходится, то при 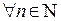интегралы 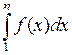ограничены, и значит, ограничены частные суммы исходного ряда: 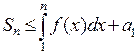. И наоборот, .

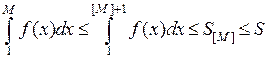Данный признак дает возможность сделать вывод о сходимости или расходимости ряда вида 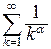, при том, что два предыдущих признака не позволяют это сделать, так как в обоих случаях здесь 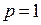. Вспомним, что несобственный интеграл 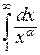сходится при и расходится при 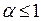. Поэтому ряд 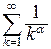сходится при и расходится при .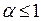

Дата добавления: 2014-01-13