
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие жесткой системы дифференциальных уравнений
Многие из рассмотренных численных методов интегрирования обыкновенных дифференциальных уравнений переносятся без изменения на системы дифференциальных уравнений. Однако в случае численного решения систем уравнений могут появиться дополнительные трудности, связанные с разномасштабностью процессов, описываемых данной системой.
Рассмотрим, например, систему двух уравнений
 ,
,  ,
,  , (8.71)
, (8.71)
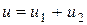 ,
,
где 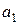 , и
, и  положительные постоянные.
положительные постоянные.
Система (8.71) имеет решение
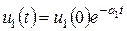 ,
,  ,
,
монотонно убывающие с ростом 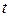 . Предположим, что
. Предположим, что  . Тогда компонента
. Тогда компонента 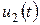 затухает гораздо быстрее, чем
затухает гораздо быстрее, чем 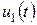 , и, начиная с некоторого
, и, начиная с некоторого 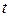 , поведение решения
, поведение решения 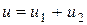 почти полностью определяется компонентой
почти полностью определяется компонентой 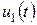 . Однако оказывается, что при решении системы (8.71) разностным методом шаг интегрирования
. Однако оказывается, что при решении системы (8.71) разностным методом шаг интегрирования 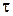 определяется, как правило, компонентой
определяется, как правило, компонентой 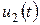 , не существенной с точки зрения поведения решения системы. Например, метод Эйлера
, не существенной с точки зрения поведения решения системы. Например, метод Эйлера
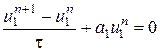 ,
,  , (8.72)
, (8.72)
где  ,
,  , будет устойчив, если шаг
, будет устойчив, если шаг 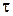 удовлетворяет одновременно двум неравенствам
удовлетворяет одновременно двум неравенствам  ,
, 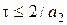 . Поскольку
. Поскольку  , условие устойчивости приводит к ограничению
, условие устойчивости приводит к ограничению 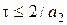 .
.
В приведенном примере на самом деле каждое уравнение следует решать отдельно со своим шагом интегрирования. Однако аналогичные трудности возникают и при решении любой системы обыкновенных дифференциальных уравнений
 , (8.73)
, (8.73)
если матрица этой системы имеет большой разброс собственных чисел 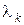 .
.
Сформулируем определение жесткой системы уравнений. Рассмотрим сначала систему (8.73) с постоянной, т.е. не зависящей от 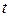 матрицей
матрицей  . Система дифференциальных уравнений (8.73) с постоянной матрицей
. Система дифференциальных уравнений (8.73) с постоянной матрицей 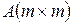 называется жесткой, если
называется жесткой, если
1)  ,
, 
(т.е. система асимптотически устойчива по Ляпунову),
2) отношение 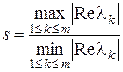
велико. Здесь 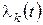 ,
, 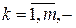 собственные числа матрицы
собственные числа матрицы .
.
Число 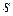 называется числом жесткости системы (8.73). Второе требование не указывает границу для
называется числом жесткости системы (8.73). Второе требование не указывает границу для 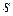 , начиная с которой система становится жесткой. Если матрица
, начиная с которой система становится жесткой. Если матрица  зависит от
зависит от 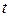 , то
, то  ,
,  . При каждом
. При каждом 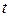 можно определить число жесткости
можно определить число жесткости
 .
.
В этом случае свойство жесткости может зависеть от длины отрезка интегрирования. Система

называется жесткой на интервале 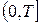 , если
, если  ,
,  , для всех
, для всех 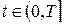 и число
и число  велико.
велико.
Так же как и в случае системы (8.72), нетрудно прийти к следующему выводу. Решение жесткой системы содержит как быстро убывающие, так и медленно убывающие составляющие. Начиная с некоторого  решение системы почти полностью определяется медленно убывающей составляющей. Однако при использовании явных разностных методов быстро убывающая составляющая отрицательно влияет на устойчивость, что вынуждает брать шаг интегрирования
решение системы почти полностью определяется медленно убывающей составляющей. Однако при использовании явных разностных методов быстро убывающая составляющая отрицательно влияет на устойчивость, что вынуждает брать шаг интегрирования 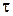 слишком мелким.
слишком мелким.
Выход из этой парадоксальной ситуации был найден в применении неявных абсолютно устойчивых разностных методов. Например, систему (8.72) можно решить с помощью неявного метода Эйлера
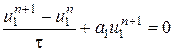 ,
, 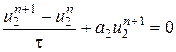 ,
,
который устойчив при всех  . Поэтому шаг интегрирования здесь можно выбрать, руководствуясь лишь соображениями точности, а не устойчивости
. Поэтому шаг интегрирования здесь можно выбрать, руководствуясь лишь соображениями точности, а не устойчивости
|
Дата добавления: 2014-01-13; Просмотров: 943; Нарушение авторских прав?; Мы поможем в написании вашей работы!