
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Разностных схем
АППРОКСИМАЦИИ. СХОДИМОСТЬ, УСТОЙЧИВОСТЬ
АППРОКСИМАЦИЯ ПРОИЗВОДНЫХ, ТОЧНОСТЬ
ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ.
КОНЕЧНО-РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ
Лекция №3
К сожалению, лишь немногие краевые задачи математической физики удается решить аналитически без применения ЭВМ в силу их сложности. Поэтому численные методы решения задач математической физики играют очень важную роль в практике инженерных расчетов.
При численных методах решения дифференциальных уравнений искомое решение получается в виде таблицы числовых значений искомой функции в некотором заданном наборе значений аргументов (в узловых точках сетки).
Схема построения решения дифференциальных уравнений в частных производных методом конечных разностей следующая:
 |  |  | |||
 Формирование Задание начальных Построение конечно-разностных
Формирование Задание начальных Построение конечно-разностных
 сетки значений искомых аналогов дифф.ур-ний в частных
сетки значений искомых аналогов дифф.ур-ний в частных
 переменных производных и граничных
переменных производных и граничных
 и граничных условий
и граничных условий
 |
 Процесс решения
Процесс решения
Процесс построения вычислительного решения:














 Исх.диф.ур-е ч.пр Дискретизация Система Алгоритм Приближенное
Исх.диф.ур-е ч.пр Дискретизация Система Алгоритм Приближенное
 и граничны е алгебр. решения решение
и граничны е алгебр. решения решение



 условия ур-ний
условия ур-ний
 |  |
Метод конечных разностей. Конечно-разностная аппроксимация производных для функций одного и двух переменных. Точность аппроксимации. Примеры
При численных методах решения дифференциальных уравнений исходное дифференциальное уравнение заменяется некоторым конечно-разностным аналогом, т.е. производные аппроксимируются конечными разностями в некоторых узловых точках (на некоторой сетке) (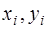 ), например,
), например, 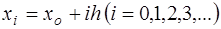 . Причем, численными методами удается получить только частные решения дифференциальных уравнений.
. Причем, численными методами удается получить только частные решения дифференциальных уравнений.
По определению 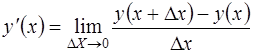 характеризует скорость изменения функции
характеризует скорость изменения функции 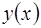 .
.
Численное решение дифференциальных уравнений математической физики методом конечных разностей проводится в два этапа: 1)разностная аппроксимация дифференциального уравнения на сетке – написание разностной схемы (дискретизация); 2) решение на ЭВМ разностных уравнений, представляющих собой системы линейных (нелинейных) разностных уравнений высокого порядка специального вида (плохая обусловленность, ленточная структура). В некоторых случаях (задача Коши) значения функции 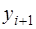 в последующей точке
в последующей точке 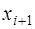 выражаются непосредственно через предыдущие значения
выражаются непосредственно через предыдущие значения 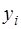 без решения системы уравнений (разностных). Если исходное дифференциальное уравнение нелинейное, то конечно-разностные аппроксимации приводят к системе нелинейных уравнений. Определим конечно-разностные аппроксимации производных.
без решения системы уравнений (разностных). Если исходное дифференциальное уравнение нелинейное, то конечно-разностные аппроксимации приводят к системе нелинейных уравнений. Определим конечно-разностные аппроксимации производных.
уi+1 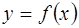 Для получения этих
Для получения этих
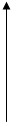

 yi
yi
 У уi-1 выражений
У уi-1 выражений для аппроксима-
для аппроксима-
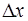 ции определим разложения
ции определим разложения
 х
х
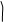


 х в ряд Тейлора
х в ряд Тейлора 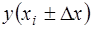
а хi-1 xi xi+1 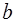 в окрестности
в окрестности 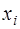 :
:
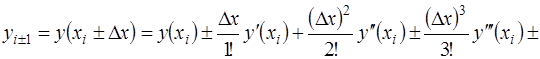 (1)
(1)
При малых 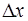 , отбросив члены (малые) более высоких порядков (пренебрегая ими) в (1), получим выражения:
, отбросив члены (малые) более высоких порядков (пренебрегая ими) в (1), получим выражения:
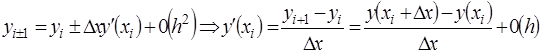
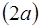
выражение для первой производной (производная, взятая с шагом вперед);
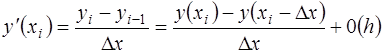 (2 б)
(2 б)
выражение для левой производной (производная, взятая с шагом назад).
Точность этих аппроксимаций порядка 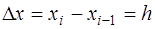
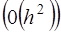 .
.
Можно построить аппроксимации более высокого порядка:
*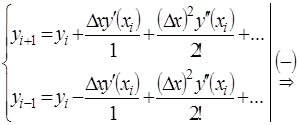
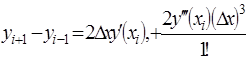



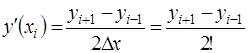 (2в)+0(h2)
(2в)+0(h2)


- центрально-разностная аппроксимация. Можно получить и другие аппроксимации, например, 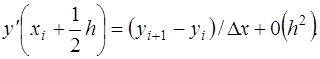
Если в (*) сложить два разложения с учетом членов только 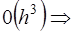
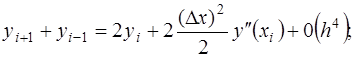
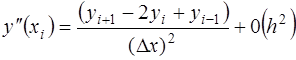 (3)
(3)
Для получения аппроксимаций для первой и второй производных были использованы значения функции в трех точках. Основываясь на выражениях для 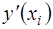 и
и 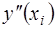 и формальные правила дифференцирования можно получить аппроксимации любых производных:
и формальные правила дифференцирования можно получить аппроксимации любых производных:
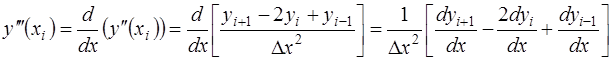 =
=
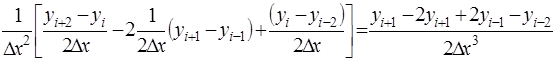 (4)
(4)
использовали (2в)
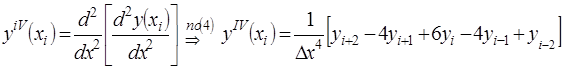 (5)
(5)
Аналогичным образом, используя разложение в ряд Тейлора функций многих переменных, можно получить конечно-разностные аппроксимации частных производных. Например, для двух переменных:
y
h1





fij h 0 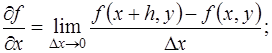 Þ
Þ

 fi+1,j=
fi+1,j=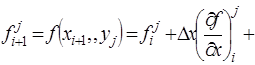
 xi –h1 xi xi +h1 x
xi –h1 xi xi +h1 x
+ 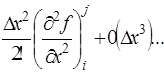



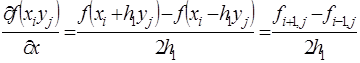


 i,j
i,j
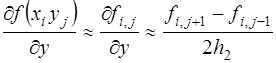 (6)
(6)

 i,j
i,j 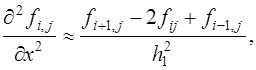
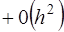

 i,j
i,j 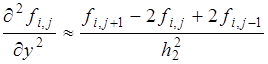

 i,j
i,j 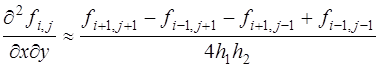
В полученных выражениях (6) отброшены члены порядка

 i,j
i,j 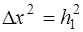 (или
(или 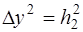 ).Они являются центрально- разностными аппроксимациями (формулами). Возможны другие аппроксимации (более точные).
).Они являются центрально- разностными аппроксимациями (формулами). Возможны другие аппроксимации (более точные).
Конфигурацию узлов, используемую для составления разностной схемы (разностных алгебраических уравнений), называют шаблоном. Для одной и той же задачи (дифференциальные уравнения) можно составить много разностных схем (разные шаблоны)
 |
 i-1 I, j+1 I+1 I,j+1
i-1 I, j+1 I+1 I,j+1
 |
j+1
i-1 I+1
 I,j;
I,j;
I,j
-1 0 1 1 -2 1








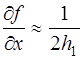 [ ];
[ ]; 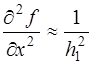 [ ];
[ ];
i-1 i,j i+1 i+1 i, j i-1
 | 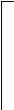 | 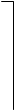 | |||






 1 i,j+1 1
1 i,j+1 1




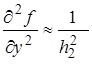 i,j -2;
i,j -2; 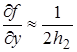 i,j 0 (7)
i,j 0 (7)




 1 i,j-1 -1
1 i,j-1 -1
Информацию о коэффициентах при 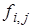 и
и 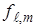 в конечно-разностных выражениях (6) удобно представлять с помощью вычислительных шаблонов типа (7). Из этих элементов строятся более сложные вычислительные шаблоны для дифф. Уравнений. Эти шаблоны имеют погрешность порядка
в конечно-разностных выражениях (6) удобно представлять с помощью вычислительных шаблонов типа (7). Из этих элементов строятся более сложные вычислительные шаблоны для дифф. Уравнений. Эти шаблоны имеют погрешность порядка 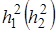 .
.
Конечно-разностные аппроксимации являются только некоторыми приближениями значений производных, т.е. допускаются погрешности (они имеют разную точность аппроксимации (см. (2)-(6)). Имеются три источника погрешностей, связанных с численной аппроксимацией:
1) погрешность округления обусловлена ограничениями на представление чисел в используемой ЭВМ (число значащих цифр ограничено);
2) погрешность усечения (дискретизации) связана с тем, что для аппроксимации функции вместо бесконечных рядов часто используется лишь несколько первых их членов (не зависит от ЭВМ);
3) погрешность распространения является результатом накопления погрешностей, появившихся на предыдущих этапах счета.
Указанные три источника погрешностей являются причиной наблюдаемых ошибок двух типов:
1) локальная ошибка - сумма погрешностей, вносимых в вычислительный процесс на каждом шаге вычислений (разность между вычисленным решением и теоретическим решением, определяемыми одними и теми же данными в точке 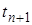 :
: 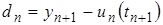 ;
;
2) глобальная ошибка – разность между вычисленным и точным решениями на каждом этапе реализации численного алгоритма, определяющая суммарную погрешность, накопившуюся с момента начала вычислений 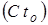 :
: 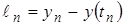 .
.
Фундаментальным понятием при оценке точности численного метода является его порядок, который определяется в терминах локальной ошибки, получаемой при применении метода к задачам с гладкими решениями. Говорят, что метод имеет порядок 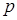 , если существует число С, такое, что для локальной ошибки выполняется
, если существует число С, такое, что для локальной ошибки выполняется 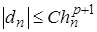 , где С – не зависит от номера шага
, где С – не зависит от номера шага 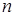 и величины шага
и величины шага 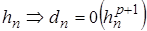 .
.
Расчетные формулы численного метода согласуются с разложением в ряд Тейлора до членов порядка 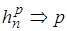 - порядок метода. (8)
- порядок метода. (8)
Метод Эйлера имеет первый порядок (р=1): 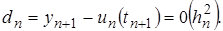
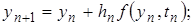

Если локальная ошибка есть 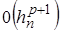 , то глобальная ошибка будет
, то глобальная ошибка будет
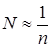 ,
, 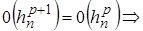 поэтому в определении прядка в показателе было взято
поэтому в определении прядка в показателе было взято 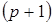 , а не
, а не 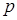 .
.
Примеры аппроксимации
Уравнение изгиба балки (1.1) 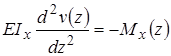 в разностном виде может быть представлено в виде:
в разностном виде может быть представлено в виде: 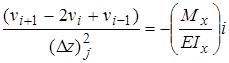 (1.1¢)
(1.1¢)
При заданном (определенном) 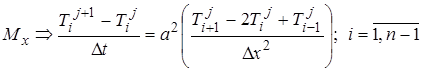
Для статически неопределимых систем (количество неизвестных превышает количество уравнений равновесия) совместно решаются




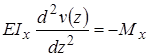 и
и 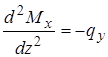 или
или 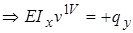 , конечно-разностный аналог которого имеет вид:
, конечно-разностный аналог которого имеет вид:
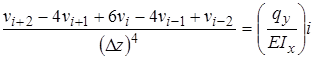
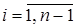 (1.1²)
(1.1²)
Эти соотношения записаны для всех внутренних точек балки. К ним добавляются соотношения, полученные из краевых условий, и получается замкнутая система алгебраических уравнений. Порядок системы равен числу неизвестных 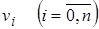 .
.
Метод Рунге-Кутта
В основе получения вычислительных схем метода Рунге-Кутта лежит разложение функции 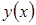 в ряд Тейлора и последующее преобразование производных к членам, не содержащим производные, используя значения производных низкого порядка и функции
в ряд Тейлора и последующее преобразование производных к членам, не содержащим производные, используя значения производных низкого порядка и функции 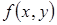 в некоторых внутренних точках, в урезанном ряду. Например, как в случае модифицированного метода Эйлера. Вычислительная схема называется схемой
в некоторых внутренних точках, в урезанном ряду. Например, как в случае модифицированного метода Эйлера. Вычислительная схема называется схемой 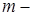 го порядка, если она получена преобразованием отрезка ряда Тейлора, содержащего производные функции
го порядка, если она получена преобразованием отрезка ряда Тейлора, содержащего производные функции 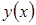 до
до 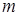 -го порядка включительно. Наиболее распространенным среди них является метод, при котором удерживаются все члены, включая
-го порядка включительно. Наиболее распространенным среди них является метод, при котором удерживаются все члены, включая 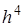 . Это метод четвертого порядка точности, для которого ошибка на каждом шаге имеет порядок
. Это метод четвертого порядка точности, для которого ошибка на каждом шаге имеет порядок 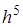 . Формула имеет вид:
. Формула имеет вид:
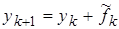 , где + 0
, где + 0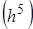 (13)
(13)
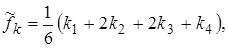
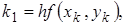
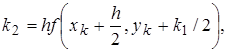
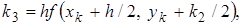
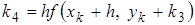 .
.
Для формул Рунге-Кутта справедлива следующая оценка величины главного члена погрешности для схемы 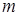 -го порядка
-го порядка
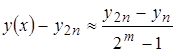 , где (14)
, где (14)
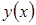 - точное значение решения в точке х;
- точное значение решения в точке х; 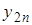 - приближенное решение в точке
- приближенное решение в точке 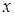 , найденное с шагом
, найденное с шагом 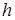 ;
; 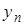 - приближенное значение решения в точке
- приближенное значение решения в точке 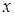 , найденное с шагом 2
, найденное с шагом 2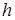 .
.
При выборе шага для устойчивости метода в качестве критерия устойчивости для схем третьего и четвертого порядков может быть принята величина
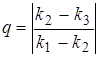 . Если
. Если 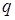 ~
~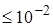 , то шаг выбран правильно; в противном случае шаг уменьшается.
, то шаг выбран правильно; в противном случае шаг уменьшается.
Сходимость, устойчивость разностных схем. Точность решения.
Важный вопрос, относящийся к численным решениям, состоит в том, до какой степени мы можем гарантировать, что численные решения дифференциального уравнения в частных производных будет близко к точному решению, а также при каких условиях это численное решение совпадает с точным. Очевидный ответ на вторую часть этого вопроса состоит в том, что следует требовать, чтобы приближение (численное) решение сходимости к точному при 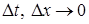 (размеры элементов сетки
(размеры элементов сетки 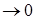 ). Однако сходимость очень трудно установить таким прямым путем, поэтому обычно используют обходной путь, который связан с требованием о том, чтобы система алгебраических уравнений, полученных в результате процесса дискретизации, была cогласованной с исходным дифференциальным уравнением в частных производных.
). Однако сходимость очень трудно установить таким прямым путем, поэтому обычно используют обходной путь, который связан с требованием о том, чтобы система алгебраических уравнений, полученных в результате процесса дискретизации, была cогласованной с исходным дифференциальным уравнением в частных производных.
Согласованность означает, что при помощи разложения в ряд Тейлора процесс дискретизации может быть обращен с целью восстановления исходного дифференциального уравнения. Кроме того, алгоритм, который служит для решения алгебраических уравнений, должен быть устойчивым. Таким образом, чтобы судить о сходимости, можно привлечь схему:
 |
 Согласованность+устойчивость
Согласованность+устойчивость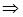 сходимость
сходимость
Концептуальная связь между согласованностью, устойчивостью и сходимостью следующая:







 Исходное дифф.уравнение дискретизация Система алгебраических
Исходное дифф.уравнение дискретизация Система алгебраических
в частных производных



 L (Т) Согласованность уравнений
L (Т) Согласованность уравнений
 |  |
Устойчивость





 ??
??
Приближенное Сходимость Точное решение Тточ.



 решение при
решение при 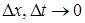
Решение алгебраических уравнений, аппроксимирующих заданное дифференциальное уравнение, называют сходящимся, если это приближение (численное) решение приближается к точному решению дифференциального уравнения для любого значения независимой переменной, по мере того как размеры ячеек сетки приближаются к нулю 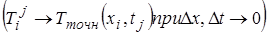
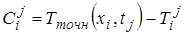 - называется ошибкой решения. Точное решение системы алгебраических уравнений является приближенным решением исходного дифф. уравнения. Для некоторого ограниченного класса задач можно установить сходимость теоретически (например, используя теорему Лакса об эквивалентности). Обычно сходимость устанавливают численными расчетами при различных размерах элементов сетки (ошибка решения должна уменьшаться до нуля при
- называется ошибкой решения. Точное решение системы алгебраических уравнений является приближенным решением исходного дифф. уравнения. Для некоторого ограниченного класса задач можно установить сходимость теоретически (например, используя теорему Лакса об эквивалентности). Обычно сходимость устанавливают численными расчетами при различных размерах элементов сетки (ошибка решения должна уменьшаться до нуля при 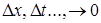 ).
).
Говорят, что система алгебраических уравнений, полученная в результате процесса дискретизации, согласуется с первоначальным дифф. уравнением, если в пределе, когда размеры ячеек сетки стремятся к нулю, система алгебраических уравнений эквивалентна дифф.уравнению в каждой из узловых точек сетки. Условие согласованности не является достаточным для сходи мости, но является необходимым.
(Ошибка аппроксимации должна 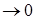 при
при 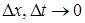 ).
).
Понятие устойчивости связано с ростом или затуханием ошибок, вносимых в расчет на любом его этапе (особенно ошибок округления, т.к. конечное число значащих цифр используется). Конкретный метод считается устойчивым, если кумулятивный эффект всех ошибок округления, возникших в процессе применения данного алгоритма, является пренебрежимо малым. Двумя наиболее употребительными методами анализа устойчивости являются матричный метод и метод Неймана. В основе обоих методов лежит возможность предсказания, будет ли иметь место рост ошибки как разности, учитывающей погрешности округления.
Обсуждение проблем сходимости, согласованности и устойчивости касалось поведения приближенного решения в пределе при 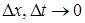 . Однако на практике приближенные решения строятся на сетке конечных размеров и соответствующая точность имеет немаловажное значение.
. Однако на практике приближенные решения строятся на сетке конечных размеров и соответствующая точность имеет немаловажное значение.
а) Один из путей определения точности конкретного алгоритма на сетке конечных размеров состоит в том, чтобы применить этот алгоритм к решению родственной, но более простой задачи, имеющей точное решение. Однако, тот алгоритм, который был достаточно точным для модельной задачи, необязательно будет столь же точным для первоначальной задачи.
б) Вторая методика оценки точности состоит в том, чтобы строить решения на последовательно измельчаемых сетках и проверять, будет ли при таком последовательном измельчении решение изменяться в рамках заранее предопределенной степени точности. Численные решения полезно сравнить с надежными экспериментальными результатами для той же самой задачи.
Можно ожидать, что в некоторых специальных случаях применение схем высокого порядка или использование мелких сеток могут привести к построению более точных решений, но еще важно время счета Þ. Вычислительную эффективность можно определить как точность, достигаемую в расчете на единицу времени исполнения.
|
Дата добавления: 2014-01-14; Просмотров: 1519; Нарушение авторских прав?; Мы поможем в написании вашей работы!