
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формы записи задачи линейного программирования
|
|
|
|
Принцип оптимальности в планировании и управлении, общая задача оптимального программирования
Линейное программирование
Слово “программирование” используется в значении “планирование”, не имеет отношения к компьютерному программированию.
Линейное программирование — это частный раздел оптимального программирования. В свою очередь оптимальное (математическое) программирование — раздел прикладной математики, изучающий задачи условной оптимизации. В экономике такие задачи возникают при практической реализации принципа оптимальности в планировании и управлении.
Необходимым условием использования оптимального подхода к планированию и управлению (принципа оптимальности) является гибкость, альтернативность производственно-хозяйственных ситуаций, в условиях которых приходится принимать планово-управленческие решения. Именно такие ситуации, как правило, и составляют повседневную практику хозяйствующего субъекта (выбор производственной программы, прикрепление к поставщикам, маршрутизация, раскрой материалов, приготовление смесей и т.д.). Суть принципа оптимальности состоит в стремлении выбрать такое планово-управленческое решение  = (х1, х2,..., xп), где xj, (j =
= (х1, х2,..., xп), где xj, (j = ) — его компоненты, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта.
) — его компоненты, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта.
Слова «наилучшим образом» здесь означают выбор некоторого критерия оптимальности, т.е. некоторого экономического показателя, позволяющего сравнивать эффективность тех или иных планово-управленческих решений. Традиционные критерии оптимальности; «максимум прибыли», «минимум затрат», «максимум рентабельности» и др.
|
|
|
Слова «учитывало бы внутренние возможности и внешние условия производственной деятельности» означают, что на выбор планово-управленческого решения (поведения) накладывается ряд условий, т.е. выбор  осуществляется из некоторой области возможных (допустимых) решений D, эту область называют также областью определения задачи.
осуществляется из некоторой области возможных (допустимых) решений D, эту область называют также областью определения задачи.
Таким образом, реализовать на практике принцип оптимальности в планировании и управлении — это значит решить экстремальную задачу вида:
max(min) f(  ), ),
| (2.1) |
 ÎD, ÎD,
| (2.2) |
где f(  ) — математическая запись критерия оптимальности — целевая функция. Задачу условной оптимизации (2.1), (2.2) обычно записывают в виде:
) — математическая запись критерия оптимальности — целевая функция. Задачу условной оптимизации (2.1), (2.2) обычно записывают в виде:
Найти максимум или минимум функции
f(  )=f(х1, х2,..., xп), )=f(х1, х2,..., xп),
| (2.3) |
при ограничениях j1 =(х1, х2,..., xп){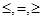 }b1,
}b1,
j2 =(х1, х2,..., xп) {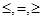 }b2, }b2,
| (2.4) |
| …. | |
jm =(х1, х2,..., xп) {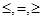 }bm, }bm,
| |
xj 0, j = 0, j =
| (2.5) |
Условие (2.5) необязательно, но его всегда при необходимости можно добиться. Обозначение {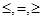 } говорит о том, что в конкретном ограничении возможен один из знаков:
} говорит о том, что в конкретном ограничении возможен один из знаков: 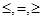 . Более компактная запись:
. Более компактная запись:
| max(min) f(х1, х2,..., xп), | (2.6) |
ji =(х1, х2,..., xп) {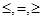 }bi, i= }bi, i=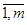
| (2.7) |
xj 0, j = 0, j =
| (2.8) |
Задача (2.6)-(2.8) — общая задача оптимального (математического) программирования, иначе — математическая модель задачи оптимального программирования, в основе построения (разработки) которой лежат принципы оптимальности и системности.
Вектор  (набор управляющих переменных xj, j =
(набор управляющих переменных xj, j = ) называется допустимым решением, или планом задачи оптимального программирования, если он удовлетворяет системе ограничений. А тот план
) называется допустимым решением, или планом задачи оптимального программирования, если он удовлетворяет системе ограничений. А тот план  (допустимое решение), который доставляет максимум или минимум целевой функции f(х1, х2,..., xп), называется оптимальным планом (оптимальным поведением, или просто решением) задачи оптимального программирования.
(допустимое решение), который доставляет максимум или минимум целевой функции f(х1, х2,..., xп), называется оптимальным планом (оптимальным поведением, или просто решением) задачи оптимального программирования.
Таким образом, выбор оптимального управленческого поведения в конкретной производственной ситуации связан с проведением с позиций системности и оптимальности экономико-математического моделирования и решением задачи оптимального программирования.
|
|
|
Задачи оптимального программирования в наиболее общем виде классифицируют по следующим признакам.
1. По характеру взаимосвязи между переменными —
а) линейные (все функциональные связи в системе ограничений и функция цели — линейные функции),
б) нелинейные (наличие нелинейности хотя бы в одном из упомянутых элементов).
2. По характеру изменения переменных —
а) непрерывные (значения каждой из управляющих переменных могут заполнять сплошь некоторую область действительных чисел),
б) дискретные (все или хотя бы одна переменная могут принимать только целочисленные значения).
3. По учету фактора времени —
а) статические (моделирование и принятие решений осуществляются в предположении о независимости от времени элементов модели в течение периода времени, на который принимается планово-управленческое решение),
б ) динамические (такое предположение достаточно аргументированно принято не может быть и необходимо учитывать фактор времени).
4. По наличию информации о переменных —
а) задачи в условиях полной определенности (детерминированные),
б) задачи в условиях неполной информации (отдельные элементы являются вероятностными величинами, однако известны или дополнительными статистическими исследованиями могут быть установлены их законы распределения),
в) задачи в условиях неопределенности (можно сделать предположение о возможных исходах случайных элементов, но нет возможности сделать вывод о вероятностях исходов).
5. По числу критериев оценки альтернатив —
а) простые, однокритериальные задачи (экономически приемлемо использование одного критерия оптимальности или удается специальными процедурами (например, «взвешиванием приоритетов») свести многокритериальный поиск к однокритериальному),
б) сложные, многокритериальные задачи.
Сочетание признаков 1—5 позволяет группировать (классифицировать) в самом общем виде задачи и методы оптимального программирования, например: 1а)2а)3а)4а)5а) — задачи и методы линейного программирования,1б)2а)3а)4a)5a) — задачи и методы нелинейного программирования, 1а)2б)3а)4а)5а) — задачи и методы целочисленного (дискретного) линейного программирования и т.д.
|
|
|
Выбору метода решения конкретной задачи оптимального программирования предшествует ее классификация, т.е. отнесение к одному из классов оптимизационных задач, начиная с приведенных самых общих признаков (например, задача дискретного линейного программирования с булевыми переменными).
Развитие и совершенствование методов решения задач оптимального программирования идет от случаев типа а) к случаям типаб), в).
Наиболее изучены задачи линейного программирования, для которых разработан универсальный метод решения — метод последовательного улучшения плана (симплекс-метод), т.е. любая задача линейного программирования решается (реализуется) этим методом. Именно эти задачи в дальнейшем мы и рассмотрим.
Как отмечено выше, среди широкого класса задач оптимального программирования имеются важные подклассы задач, для которых разработаны эффективные методы решения. Наиболее изученным подклассом задач являются задачи линейного программирования.
В задаче линейного программирования (ЗЛП) требуется найти экстремум (максимум или минимум) линейной целевой функции f(  ):
):
max(min) f(  )=c1x1+c2x2+…+ cnxn, )=c1x1+c2x2+…+ cnxn,
| (2.9) |
при ограничениях (условиях):
a11x1+a12x2+…+ a1nxn {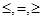 }b1, }b1,
| |
a21x1+a22x2+…+ a2nxn {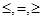 }b2, }b2,
| (2.10) |
| ……… | |
am1x1+am2x2+…+ amnxn {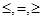 }bm, }bm,
| |
xj 0, j = 0, j =
| (2.11) |
где aij, bi, cj (i=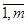 , j =
, j = )— заданные постоянные величины.
)— заданные постоянные величины.
Так записывается общая задача линейного программирования в развернутой форме; знак {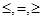 } означает, что в конкретной ЗЛП возможно ограничение типа равенства или неравенства (в ту или иную сторону).
} означает, что в конкретной ЗЛП возможно ограничение типа равенства или неравенства (в ту или иную сторону).
Систему ограничений (2.10) называют функциональными ограничениями ЗЛП, а ограничения (2.11) — прямыми.
Вектор  = (х1, х2,..., xп), удовлетворяющий системе ограничений (2.10), (2.11), называется допустимым решением, или планом ЗЛП, т.е. ограничения (2.10), (2.11) определяют область допустимых решений, или планов задачи линейного программирования (область определения ЗЛП).
= (х1, х2,..., xп), удовлетворяющий системе ограничений (2.10), (2.11), называется допустимым решением, или планом ЗЛП, т.е. ограничения (2.10), (2.11) определяют область допустимых решений, или планов задачи линейного программирования (область определения ЗЛП).
|
|
|
План (допустимое решение), который доставляет максимум или минимум целевой функции (2.9), называется оптимальным планом (оптимальным решением) ЗЛП.
Канонической формой записи задачи линейного программирования (КЗЛП) называют задачу вида (запись с использованием знаков суммирования):
Найти
max f(  )= )=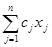
| (2.12) |
при ограничениях
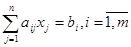
| (2.13) |
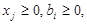 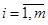 , j = , j = . .
| (2.14) |
Векторная форма записи КЗЛП имеет вид:
Найти max f(  )=CX
)=CX
при ограничениях A1x1+A2x2+…+ Anxn, = В, 
где С=(c1, c2,..., cn), Х = (x1, x2,..., xn),
СХ — скалярное произведение векторов С,Х,
Aj и В — вектор-столбцы:
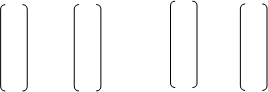
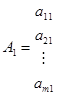 ,
, 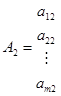 , …,
, …, 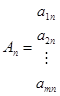 ,
, 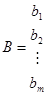 .
.
Матричная форма записи КЗЛП:
max f(  )=CX
)=CX
при условиях AX = B, X 0.
0.
Здесь С = (c1, c2,…, cn,) — вектор-строка; А=(аij) — матрица размерности т x п, столбцами которой являются вектор-столбцы Aj,

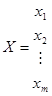 — вектор-столбец,
— вектор-столбец, 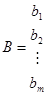 — вектор-столбец.
— вектор-столбец.
Расширенная матрица этой системы будет иметь вид:
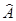 =
=
Иногда используется стандартная форма записи ЗЛП:
max(min) f(  )=CX,
)=CX,
AX B, X
B, X 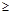 0.
0.
При этом запись X 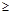 0 понимают как вектор (или вектор-столбец в зависимости от контекста), у которого все компоненты (элементы) неотрицательны.
0 понимают как вектор (или вектор-столбец в зависимости от контекста), у которого все компоненты (элементы) неотрицательны.
Приведение ЗЛП к каноническому виду осуществляется введением в левую часть соответствующего ограничения вида (2.10) k-ой дополнительной переменной xn+k 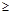 0 со знаком “-“ в случае ограничения типа
0 со знаком “-“ в случае ограничения типа 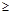 и знаком “+” в случае ограничения типа
и знаком “+” в случае ограничения типа 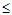 .
.
▼
Пример. Имеется задача линейного программирования
max f(  )=c1x1+c2x2, )=c1x1+c2x2,
|
a11x1+a12x2 b1, b1,
|
a21x1+a22x2 b2, b2,
|
xj 0, j = 0, j =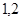
|
Представим ее в канонической форме
max f(  )=c1x1+c2x2+0x3+0x4, )=c1x1+c2x2+0x3+0x4,
|
| a11x1+a12x2+x3=b1, |
| a21x1+a22x2+x4=b2, |
xj 0, j = 0, j =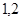
|
Расширенная матрица будет иметь вид:

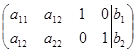
В ее составе присутствует единичная матрица.
▲
Если на некоторую переменную хr не накладывается условие неотрицательности, то делают замену переменных 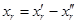 ,
,  ,
, 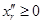 . В преобразованной задаче все переменные неотрицательные. Переход к задаче на максимум достигается изменением в случае необходимости знака у целевой функции.
. В преобразованной задаче все переменные неотрицательные. Переход к задаче на максимум достигается изменением в случае необходимости знака у целевой функции.
К математическим задачам линейного программирования приводят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов (задача о раскрое, смесях, диете и т.д.).
Изучение и понимание современных экономико-математических методов предполагает достаточно серьезную математическую подготовку экономистов. Для освоения задач и методов в пределах наших занятий необходимы знания основных понятий и элементов высшей математики, матричной и векторной алгебры.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 4137; Нарушение авторских прав?; Мы поможем в написании вашей работы!