Понятие функционального ряда

NZQRC

Часто используемые подмножества множества R: интервалы, отрезки, полуинтервалы, конечные, бесконечные, ε-окрестности.

Логические символы и общепринятые обозначения:

.

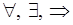Примеры.

1. Утверждение «Для любого х, взятого из отрезка [-1, 2], можно найти y на отрезке [1, 4], такое, что y = x²» записывается так

.

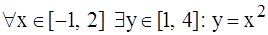Отображения множеств. Функции. Однозначность. Взаимная однозначность. Изоморфизм.

Мощность множества.

Определение. Мощностью μ(М) множества М наз. его количественная мера, обладающая след. свойствами:

1) Для конечного множества μ(М) = числу элементов в М

2) Если между А и В сущ. вз.-одн. соответствие, то μ(А) = μ(В)

3) Если сущ. вз.-одн. соответствие между А и подмножеством В, то μ(А) ≤ μ(В)

4) Если сущ. вз.-одн. соответствие между А и подмножеством В и нельзя установить вз.-одн. соответствие между А и В,

то μ(А) < μ(В)

Любое бесконечное множество содержит подмножество, которое можно пронумеровать или пост. вз.-одн. соответствие с N.

Значит, N имеет наименьшую бесконечную мощность. Множ-ва, имеющие мощность, равную мощности N, наз. счётными. Мощность счётного мн-ва обозначается 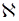₀.

Показать, μ(N) = μ(Z) = μ(Q) =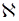₀.

Продемонстрировать нумерацию (вз. одн. соотв-е) целых чисел

N: 1 2 3 4 5 6 7 …

Z: 0 1 –1 2 -2 3 –3 …

Всякое рациональное число можно поместить в таблицу, элементы которой нумеруются начиная с угла по диагоналям. (Прокомментировать насчёт нуля, повторяемости и знаков).

						…	m	…
		±2/3
			±3/4
..
n							±m/n
..

Показать, μ(R) > 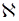₀.

Предположим противное, т.е. μ(R) = 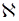₀, значит все действитель-ные числа можно пронумеровать. Рассмотрим только числа на интервале (0, 1) и предположим, что они пронумерованы:

а₁, а₂, а₃, … Запишем каждое из этих чисел в десятичной форме с неограниченным числом знаков после запятой.

а₁ = 0. α₁₁ α₁₂ α₁₃…

а₂ = 0. α₂₁ α₂₂ α₂₃…

а₃ = 0. α₁₃ α₃₂ α₃₃…

……………………

Рассмотрим число а = 0. α₁ α₂ α₃… такое, что

α₁ ≠ α₁₁, α₂ ≠ α₂₂, α₃ ≠ α₃₃,…

Тогда a ≠ a₁, a ≠ a₂, a ≠ a₃,…, а значит, числа а нет в списке. Получилось противоречие.

Рассмотреть множество всех подмножеств конечного множества.

Вывести формулу.

Терема Кантора. Мощность любого непустого множества всегда меньше мощности множества всех его подмножеств.

Доказательство от противного.

Пусть имеется взаимно-однозначное соответствие f между элементами множества М и его подмножествами:

x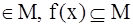. Тогда М можно разбить в объединение двух непересекающихся подмножеств: М = A U B,

А состоит из таких элементов х, для которых x,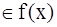

B состоит из таких элементов х, для которых x.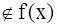

Тогда найдётся такой элемент b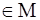, что B = f(b).

Рассмотрим, в каком из подмножеств A или В находится элемент b.

1) Допустим, что b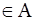. Тогда, по определению A, 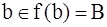, что невозможно, так как А∩В = Ø.

2) Допустим, что b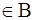. Тогда, по определению В, 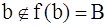, что невозможно.

Получилось противоречие. Теорема доказана.

Дать определения континуума и гиперконтинуума 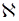₁ и 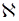₂. Рассказать о континуум-гипотезе.

Теорема. μ(R) = 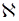₁.

Док-во. Рассмотрим множество действительных чисел в интер-вале (0, 1). Такие числа в двоичной форме имеют однозначную запись в виде 0. α₁ α₂ α₃…, где α₁, α₂, α₃ … - либо 1, либо 0. Рассмотрим такое число:

а = 0. 1 0 1 1 0 0 0 1 0 1 …

N = { 1 2 3 4 5 6 7 8 9 10 … }

f(a) = { 1 3 4 8 10 … } .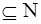

Видим, что имеется взаимно-однозначное соответствие f между действительными числами а из интервала (0, 1) и подмножествами f(a) множества натуральных чисел, ч.т.д.

Теперь установим взаимно-однозначное соответствие между интервалом (0, 1) и всей числовой осью. Согнём интервал (0, 1) в полуокружность и расположим над числовой осью, как показано на рисунке:

R

Отметить, что мощность гиперконтинуума имеет множество всех функций на отрезке.

Пусть задана последовательность функций вида

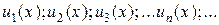
Функциональным рядом называется выражение

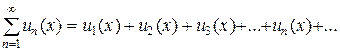(1)

Областью определения ряда называется множество значений переменной x, при которых определены все члены ряда. Возьмем некоторое значение и подставим его в ряд (1) получим числовой ряд. Этот ряд может сходиться, а может и расходиться. Множество значений переменной x, для которых ряд (1) сходится называется областью сходимости ряда. Определение области сходимости - сложная задача и мы ограничимся лишь упоминанием о ней. В области сходимости ряда сумма ряда является некоторой функцией, которую мы обозначим S(x). Определяется она так же, как и для числового ряда. Введем частичную сумму из n первых членов ряда.

Определение. Предел последовательности s_n, если он существует, называется суммой ряда (1).

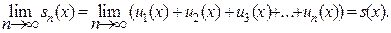(2)

Отбросим n первых членов ряда (1). Оставшийся ряд называется остатком и обозначается r_n. Т. е.

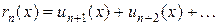
Теорема. Для того чтобы ряд сходился необходимо и достаточно, чтобы при n®¥ сумма остатка ряда стремилась к нулю.

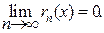
Без доказательства.

Пример. Рассмотрим ряд

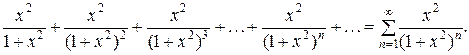
Этот ряд является геометрической прогрессией, у которой

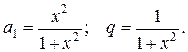
При x¹0 выполняется условие 0<q<1. И сумма ряда равна S(x)=1. При x=0 сумма ряда равна S(0)=0. Область сходимости ряда - вся числовая ось. Сумма ряда разрывная функция. Функция имеет разрыв при x=0.

Из данного примера видно, что обращаться с функциональными рядами так просто нельзя. В частности, если заменить ряд частичной суммой ряда, состоящего из непрерывных функций, получим непрерывную функцию. В то время как сумма функционального ряда может оказаться разрывной. Для того чтобы не возникали подобные неприятности, нужно ввести для функциональных рядов понятие равномерной сходимости.

Определение. Пусть сумма ряда равна S(x) на [a,b]. Функциональный ряд называется равномерно-сходящимся на [a,b], если для любого e>0 существует номер N, такой что при всех n> N и всех xÎ[a,b], выполняется неравенство

.

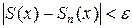Данное определение носит абстрактный характер и пользоваться им не просто. Поэтому введем более простое понятие, которое является достаточным для равномерной сходимости.

Определение. Если для функционального ряда (1) существует сходящийся числовой ряд (2) с положительными членами

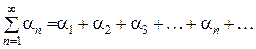(2)

такой, что для всех n и всех xÎ[a,b] выполняется неравенство

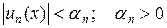
то говорят, что ряд (2) мажорирует ряд (1) на [a,b].

Дата добавления: 2014-01-14